10 Of 320
interactiveleap
Sep 16, 2025 · 5 min read
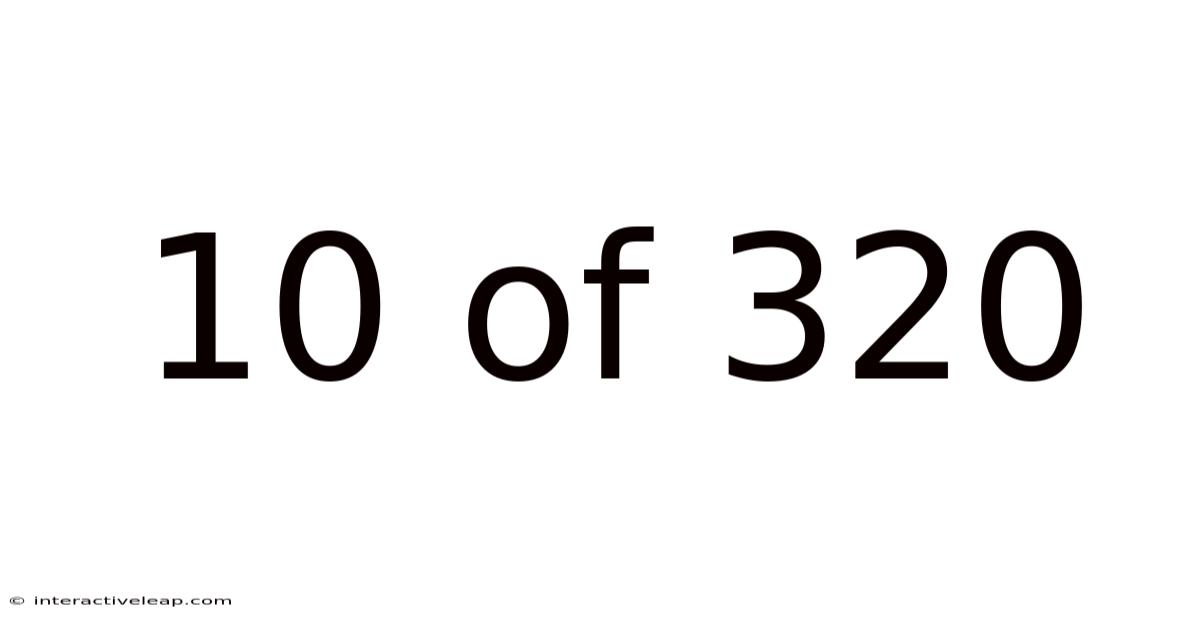
Table of Contents
Decoding the Enigma: Understanding the Fraction 10/320 and its Implications
The seemingly simple fraction 10/320 might appear insignificant at first glance. However, understanding this fraction and its various representations unveils a wealth of mathematical concepts and practical applications, spanning from basic arithmetic to advanced statistical analysis. This article delves deep into the intricacies of 10/320, exploring its simplification, decimal representation, percentage equivalent, and real-world applications. We'll also touch upon related concepts to provide a comprehensive understanding of this seemingly simple yet surprisingly insightful fraction.
Introduction: Unveiling the Simplicity Within Complexity
The fraction 10/320, at its core, represents a ratio: 10 parts out of a total of 320 parts. This seemingly straightforward representation opens doors to a broader understanding of ratios, proportions, and their applications in various fields. This article will systematically dissect this fraction, simplifying it, converting it to other forms, and exploring its contextual meaning. We'll be focusing on the core mathematical concepts, demonstrating how seemingly simple fractions can lead to a deeper appreciation of mathematical principles.
Step-by-Step Simplification of 10/320
The first crucial step in understanding 10/320 is simplifying it to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (10) and the denominator (320). The GCD is the largest number that divides both 10 and 320 without leaving a remainder.
-
Finding the GCD: We can find the GCD through prime factorization.
- 10 = 2 x 5
- 320 = 2 x 2 x 2 x 2 x 2 x 2 x 5 = 2<sup>6</sup> x 5
-
Identifying Common Factors: Both 10 and 320 share a common factor of 2 and 5. Therefore, their GCD is 10 (2 x 5).
-
Simplifying the Fraction: Dividing both the numerator and the denominator by the GCD (10):
10 ÷ 10 = 1 320 ÷ 10 = 32
Therefore, the simplified form of 10/320 is 1/32. This simplified fraction represents the same ratio but in a more concise and manageable form.
Decimal Representation and Percentage Equivalent
Converting the simplified fraction 1/32 to its decimal equivalent involves dividing the numerator (1) by the denominator (32):
1 ÷ 32 = 0.03125
To express this as a percentage, we multiply the decimal by 100:
0.03125 x 100 = 3.125%
This means that 10/320 represents 3.125% of the whole. This percentage representation is useful for comparing proportions and expressing the fraction in a readily understandable context.
Real-World Applications of 10/320 (or 1/32)
The fraction 1/32, the simplified form of 10/320, has various real-world applications across numerous fields. Here are a few examples:
-
Probability and Statistics: Imagine a scenario with 32 equally likely outcomes. The probability of a specific event occurring is 1/32. This could represent anything from drawing a specific card from a deck (after accounting for the probability of drawing a specific suit or number), to the chance of winning a lottery with 32 possible outcomes.
-
Measurement and Scaling: In engineering and design, 1/32 might represent a scale factor. A blueprint might be drawn at 1/32 scale, meaning that 1 unit on the blueprint represents 32 units in reality.
-
Mixing Ratios: In chemistry and cooking, the fraction 1/32 could define a mixing ratio. For instance, 1 part of ingredient A might be mixed with 32 parts of ingredient B.
-
Finance and Investments: Imagine an investment that yields a return of 1/32 of the initial investment. This fractional return can then be further analyzed to calculate the percentage return and compare it with other investments.
Further Mathematical Explorations: Connecting to Broader Concepts
The fraction 10/320, and its simplified form 1/32, provides a springboard to explore several other mathematical concepts:
-
Continued Fractions: The fraction 1/32 can be expressed as a continued fraction, offering a unique representation. While complex, this representation is valuable in number theory and approximation theory.
-
Geometric Series: The fraction can be incorporated into geometric series to demonstrate summation and convergence concepts. This connects the seemingly simple fraction to more complex mathematical structures.
-
Proportions and Ratios: The core understanding of ratios and proportions is central to understanding fractions like 10/320. The ability to manipulate and simplify these ratios is crucial in solving various mathematical problems.
Frequently Asked Questions (FAQs)
-
Q: What is the simplest form of 10/320?
- A: The simplest form is 1/32.
-
Q: How do I convert 10/320 to a decimal?
- A: Simplify to 1/32, then divide 1 by 32 to get 0.03125.
-
Q: What is the percentage equivalent of 10/320?
- A: It is 3.125%.
-
Q: Are there any real-world examples of using this fraction?
- A: Yes, it can be used in probability, scaling, mixing ratios, and financial calculations.
-
Q: Can 10/320 be expressed as a continued fraction?
- A: Yes, though it would be a simple continued fraction due to the nature of the simplified fraction 1/32.
Conclusion: A Deeper Appreciation of Fractions
The humble fraction 10/320, through simplification and conversion, reveals its importance and utility in various mathematical and real-world applications. Its simplicity belies a depth that extends to fundamental mathematical concepts such as ratios, proportions, probabilities, and even advanced topics like continued fractions. By meticulously dissecting this fraction, we've gained a more profound understanding not just of 10/320 itself, but of the underlying principles that govern the world of fractions and their significance in broader mathematical contexts. The journey from 10/320 to its simplified form, 1/32, and then to its decimal and percentage equivalents highlights the power of mathematical simplification and the versatility of fractional representation in our daily lives. This seemingly simple fraction demonstrates that even the most basic mathematical elements hold hidden depths and potential for deeper exploration and understanding. It encourages us to appreciate the interconnectedness of mathematical concepts and their relevance to the world around us.
Latest Posts
Latest Posts
-
180 Square Rooted
Sep 16, 2025
-
Nanograms To Grams
Sep 16, 2025
-
15 Of 42
Sep 16, 2025
-
Rad S Hz
Sep 16, 2025
-
Cousin In French
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 320 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.