100 X 1000
interactiveleap
Sep 20, 2025 · 5 min read
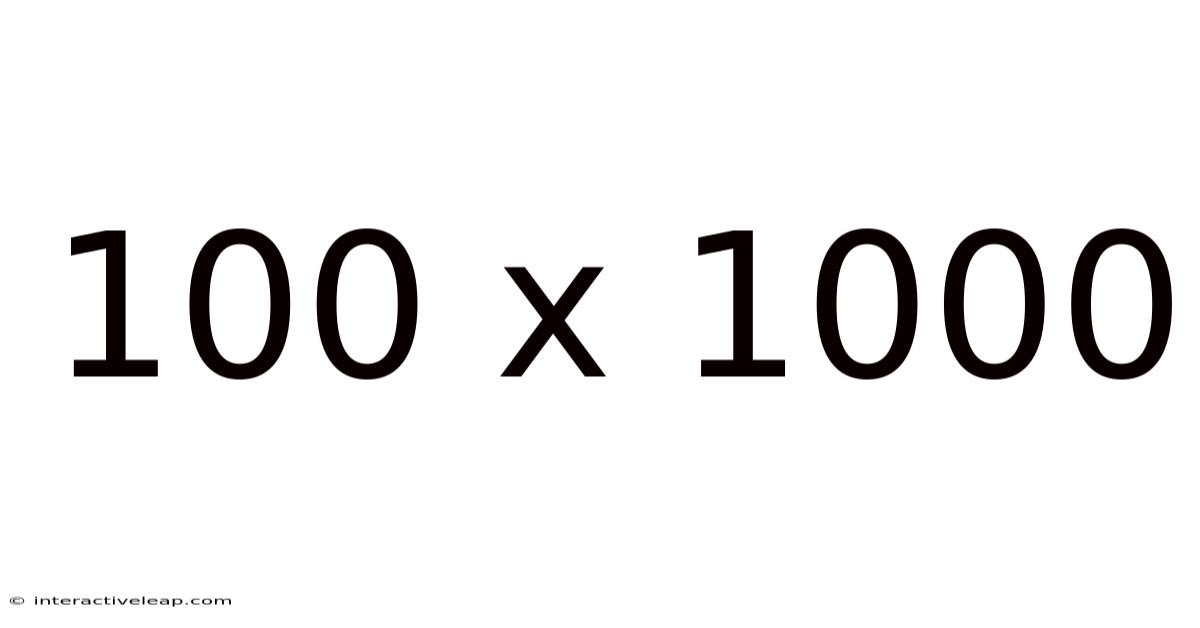
Table of Contents
Decoding 100 x 1000: A Deep Dive into Multiplication, Area, and Real-World Applications
Understanding the seemingly simple calculation of 100 x 1000 opens a door to a vast world of mathematical concepts, practical applications, and problem-solving skills. This article will explore this calculation in depth, examining its foundational principles, its relevance in various fields, and its implications for developing a stronger mathematical understanding. We’ll move beyond the simple answer to uncover the underlying concepts and real-world scenarios where this type of calculation proves invaluable.
I. Introduction: The Fundamentals of Multiplication
At its core, 100 x 1000 represents a multiplication problem. Multiplication is a fundamental arithmetic operation that essentially involves repeated addition. When we say 100 x 1000, we're asking: what is the result of adding 100 to itself 1000 times? While manually performing this addition would be incredibly tedious, the beauty of multiplication lies in its efficiency. This single operation provides the answer swiftly: 100,000.
This seemingly straightforward calculation forms the basis for numerous more complex mathematical operations and real-world applications. Let's delve deeper into the underlying principles.
II. Visualizing 100 x 1000: The Concept of Area
One excellent way to visualize 100 x 1000 is through the concept of area. Imagine a rectangle with one side measuring 100 units (e.g., meters, centimeters, or any unit of length) and the other side measuring 1000 units. The area of this rectangle is calculated by multiplying the length and width: 100 x 1000 = 100,000 square units. This visualization provides a concrete representation of the abstract concept of multiplication. We can literally see the result as the space enclosed within the rectangle.
This connection between multiplication and area is crucial in numerous fields, including:
- Construction and Engineering: Calculating the area of land plots, building foundations, or flooring requires multiplication.
- Agriculture: Determining the size of fields for planting or calculating fertilizer needs relies on area calculations.
- Cartography: Mapping and geographical analysis involve working extensively with areas and spatial measurements.
- Computer Graphics: Creating and manipulating images and 3D models relies heavily on area and volume calculations.
III. Breaking Down the Calculation: Place Value and Powers of Ten
Understanding place value is essential for grasping the efficiency of multiplying numbers like 100 and 1000. Both numbers are powers of ten:
- 100 = 10² (10 multiplied by itself twice)
- 1000 = 10³ (10 multiplied by itself three times)
Therefore, 100 x 1000 can be rewritten as 10² x 10³ = 10⁽²⁺³⁾ = 10⁵ = 100,000. This demonstrates the power of exponential notation and how understanding powers of ten simplifies calculations significantly. This principle extends to much larger numbers, making complex calculations more manageable.
IV. Real-World Applications Beyond Area: Exploring Diverse Scenarios
The application of 100 x 1000 extends far beyond simple area calculations. Here are some diverse examples:
- Finance: Calculating simple interest, total earnings from a fixed income over a period, or the cost of a bulk purchase. For instance, if you invest $100 and it earns 10% annually for 10 years, calculating the total earnings involves multiplication.
- Manufacturing: Determining the total number of units produced in a given time. If a factory produces 100 units per hour for 1000 hours, the total production is 100,000 units.
- Data Analysis: Scaling data sets, calculating aggregate values from large samples, or converting units of measurement.
- Scientific Research: Calculating concentrations, dosages, or statistical probabilities often involves multiplication.
V. Expanding the Concept: Proportions and Scaling
The calculation 100 x 1000 also serves as a foundation for understanding proportions and scaling. If, for instance, 100 represents 1% of a larger quantity, then 100,000 represents 100% of that quantity. This ability to scale up or down using multiplication is critical in various fields, from recipe adjustments in cooking to scaling blueprints in architecture.
VI. Connecting to Other Mathematical Concepts
Understanding 100 x 1000 provides a gateway to exploring more advanced mathematical concepts:
- Algebra: This calculation can be represented algebraically as x * y = z, where x = 100, y = 1000, and z = 100,000. This simple equation lays the foundation for solving more complex algebraic problems.
- Calculus: The concept of limits and derivatives, essential in calculus, builds upon the understanding of incremental changes and scaling, directly connected to multiplication.
- Statistics: Calculating means, standard deviations, and probabilities in statistical analysis often involves extensive use of multiplication.
VII. Problem-Solving Strategies: Applying the Knowledge
Let's consider some practical problem-solving scenarios involving the principles discussed:
Scenario 1: A farmer needs to plant 1000 rows of corn, with 100 corn stalks in each row. How many corn stalks does the farmer need to plant in total?
Solution: This problem directly translates to 100 x 1000 = 100,000 corn stalks.
Scenario 2: A construction company is building a rectangular building with dimensions of 100 meters by 1000 meters. What is the area of the building's footprint?
Solution: The area is 100 meters x 1000 meters = 100,000 square meters.
Scenario 3: A company produces 100 widgets per hour. How many widgets are produced in a 1000-hour work week?
Solution: The company produces 100 x 1000 = 100,000 widgets in a 1000-hour week.
VIII. Frequently Asked Questions (FAQ)
Q: What are some common mistakes made when dealing with multiplications like 100 x 1000?
A: A common mistake is misplacing the decimal point or incorrectly counting zeros. Carefully aligning the numbers and utilizing place value understanding helps prevent errors.
Q: How can I improve my skills in multiplication and related calculations?
A: Practice is key! Start with simpler problems and gradually increase the complexity. Utilizing visual aids, like the area method described earlier, can also enhance understanding.
Q: Are there any shortcuts or tricks for performing multiplication efficiently?
A: Yes, understanding powers of ten, as shown previously, is a significant shortcut. Also, mastering multiplication tables greatly improves speed and accuracy.
IX. Conclusion: The Enduring Significance of 100 x 1000
The seemingly simple calculation of 100 x 1000 serves as a cornerstone for understanding fundamental mathematical principles and their diverse applications. From calculating areas and scaling proportions to solving complex problems in various fields, mastering this calculation opens doors to a deeper understanding of the mathematical world and enhances problem-solving capabilities in numerous real-world scenarios. The significance extends beyond a simple numerical answer; it's about grasping the underlying concepts and applying that knowledge to solve problems creatively and efficiently. By understanding the intricacies of this seemingly basic calculation, one gains a stronger foundation for tackling more advanced mathematical challenges.
Latest Posts
Latest Posts
-
1 4 9
Sep 20, 2025
-
30 Of 57
Sep 20, 2025
-
25 Square Meters
Sep 20, 2025
-
3 0 75
Sep 20, 2025
-
Suzuki Drz 125
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 100 X 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.