100 X 0.2
interactiveleap
Sep 20, 2025 · 6 min read
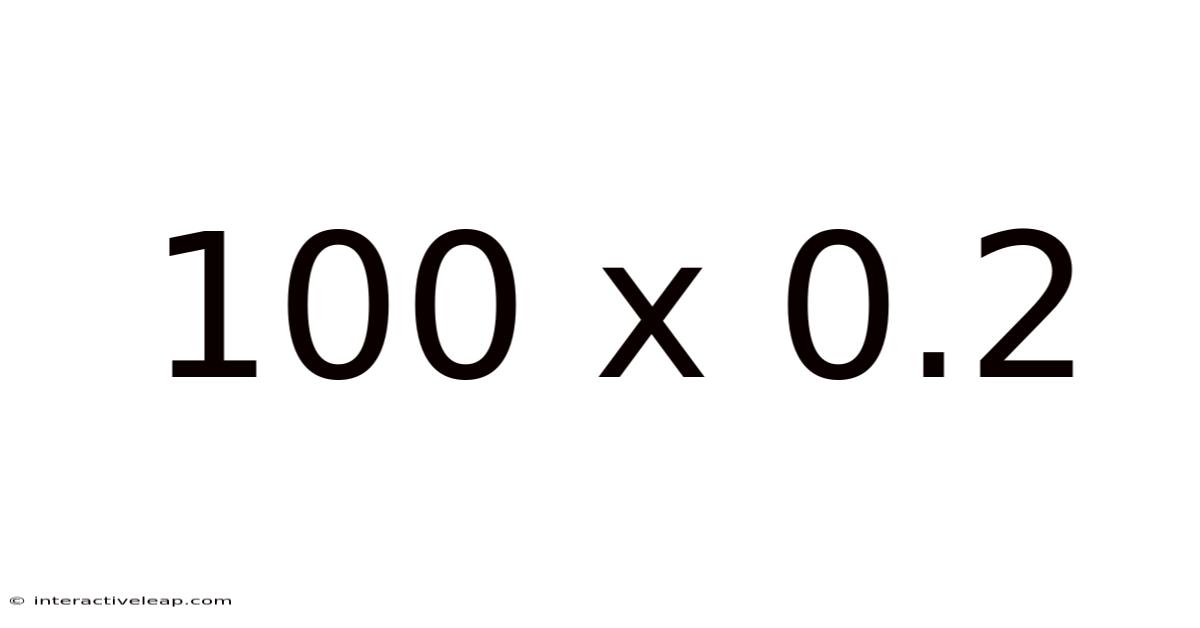
Table of Contents
Decoding 100 x 0.2: A Deep Dive into Multiplication and Decimal Operations
This article explores the seemingly simple calculation of 100 x 0.2, delving far beyond the immediate answer to uncover the underlying mathematical principles and practical applications. Understanding this seemingly basic equation provides a solid foundation for more complex mathematical concepts, particularly in areas involving decimals, percentages, and proportions. We'll examine the various methods for solving this problem, explain the logic behind each step, and explore real-world scenarios where this type of calculation is frequently used.
Understanding the Basics: Multiplication and Decimals
Before diving into the specifics of 100 x 0.2, let's refresh our understanding of fundamental concepts. Multiplication is a fundamental arithmetic operation representing repeated addition. For instance, 3 x 4 is equivalent to 3 + 3 + 3 + 3, resulting in 12. The numbers being multiplied are called factors, and the result is called the product.
Decimals, on the other hand, represent numbers that are not whole numbers. They contain a decimal point separating the whole number part from the fractional part. Understanding place value is crucial when working with decimals. Each digit to the right of the decimal point represents a decreasing power of ten: tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on.
Methods for Solving 100 x 0.2
There are several ways to solve 100 x 0.2, each offering a slightly different approach and reinforcing different mathematical skills.
Method 1: Direct Multiplication
This is the most straightforward method. We can treat 0.2 as a fraction: 2/10. Therefore, the calculation becomes:
100 x (2/10) = (100 x 2) / 10 = 200 / 10 = 20
Alternatively, we can perform the multiplication directly:
100 x 0.2 = 20
This method highlights the direct relationship between multiplication and fractions.
Method 2: Converting to Fractions
As demonstrated above, converting the decimal to a fraction simplifies the calculation. This approach emphasizes the equivalence between decimals and fractions, a crucial concept in mathematics. The steps are as follows:
- Convert the decimal to a fraction: 0.2 is equivalent to 2/10.
- Perform the multiplication: 100 x (2/10)
- Simplify the fraction: (100 x 2) / 10 = 200/10 = 20
Method 3: Using the Distributive Property
The distributive property states that a(b + c) = ab + ac. While not strictly necessary for this simple calculation, it demonstrates a broader mathematical principle. We can rewrite 0.2 as (0.1 x 2), then apply the distributive property:
100 x (0.1 x 2) = (100 x 0.1) x 2 = 10 x 2 = 20
Method 4: Understanding Percentages
0.2 can also be represented as 20%. Therefore, the calculation becomes finding 20% of 100. This approach is particularly useful for real-world applications involving percentages.
- Convert the decimal to a percentage: 0.2 = 20%
- Calculate the percentage: 20% of 100 is (20/100) x 100 = 20
This method is highly relevant in scenarios involving discounts, tax calculations, and other percentage-based problems.
Real-World Applications
The calculation 100 x 0.2, or its equivalent forms, appears frequently in everyday life and various professional fields. Here are some examples:
- Shopping Discounts: A 20% discount on a $100 item would result in a discount of $20 (100 x 0.2).
- Tax Calculations: A 20% sales tax on a $100 purchase would add $20 to the total cost.
- Financial Calculations: Calculating interest or returns on investments often involves multiplying principal amounts by decimal rates.
- Scientific Measurements: Many scientific measurements and calculations involve decimal values and multiplication.
- Engineering and Construction: Precise calculations involving dimensions and material quantities rely heavily on decimal operations.
- Data Analysis: Working with datasets often necessitates calculations involving decimal values and percentages.
Expanding on Decimal Multiplication
The principles demonstrated with 100 x 0.2 apply equally to other decimal multiplications. Consider the following:
- Multiplying by powers of 10: Multiplying a decimal by 10, 100, 1000, etc., simply moves the decimal point to the right by the number of zeros. For example, 0.2 x 10 = 2, 0.2 x 100 = 20.
- Multiplying by decimals less than 1: Multiplying by a decimal less than 1 results in a product smaller than the original number. This is because you are essentially taking a fraction of the original number.
- Multiplying decimals with multiple digits: The same principles apply when multiplying decimals with more digits. Simply perform the multiplication as if they were whole numbers, then place the decimal point in the correct position based on the total number of decimal places in the original numbers.
Addressing Common Mistakes
- Incorrect decimal placement: The most common mistake is placing the decimal point incorrectly in the product. Always count the total number of decimal places in the factors and place the decimal point accordingly in the product.
- Confusing multiplication with addition or subtraction: Ensure you are performing the correct operation.
- Rounding errors: When working with decimals, rounding errors can accumulate, especially in complex calculations. It's crucial to maintain accuracy throughout the calculation or use appropriate rounding techniques.
Frequently Asked Questions (FAQs)
Q: What is the easiest way to solve 100 x 0.2?
A: The easiest method is direct multiplication: 100 x 0.2 = 20. Alternatively, converting 0.2 to a fraction (2/10) and simplifying also provides a quick solution.
Q: Why is the product smaller than 100?
A: Because you are multiplying 100 by a number less than 1 (0.2). Multiplying by a fraction or a decimal less than one always results in a smaller product.
Q: How can I use this knowledge to solve other problems?
A: The principles of decimal multiplication are applicable to various situations involving percentages, discounts, taxes, interest calculations, and many more real-world problems. Practice applying these principles to different scenarios to build your mathematical skills.
Q: What if I have to multiply a large number by a decimal?
A: Use the standard multiplication algorithm, treating the numbers as whole numbers initially and then carefully placing the decimal point in the final answer based on the total number of decimal places in the original numbers.
Conclusion
The seemingly simple calculation of 100 x 0.2 provides a gateway to understanding fundamental mathematical concepts related to multiplication, decimals, fractions, and percentages. By exploring different solution methods and real-world applications, we gain a deeper appreciation for the practical utility of these calculations. Mastering this basic operation forms a solid foundation for tackling more complex mathematical problems and confidently applying mathematical skills in diverse fields. The key takeaway is not just the answer (20), but the underlying principles and their wide-ranging applicability. Remember to practice regularly, and you'll soon find yourself proficient in handling decimal multiplications with ease.
Latest Posts
Latest Posts
-
33 Of 34567
Sep 20, 2025
-
1 8 In Fraction
Sep 20, 2025
-
3 Of 70000
Sep 20, 2025
-
25 Of 340
Sep 20, 2025
-
Definition Sensory Language
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 100 X 0.2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.