10 Of 24000
interactiveleap
Sep 23, 2025 · 6 min read
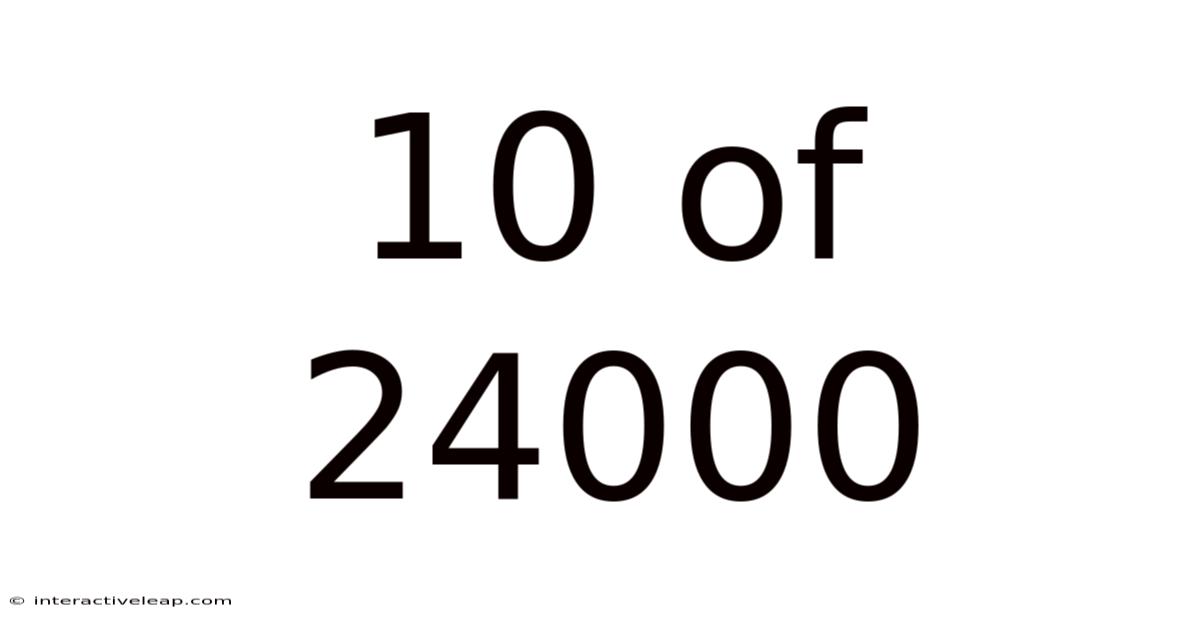
Table of Contents
Decoding 10 out of 24000: Understanding Ratios, Proportions, and their Real-World Applications
Understanding ratios and proportions is fundamental to numerous aspects of life, from cooking and construction to finance and scientific research. This article delves deep into the seemingly simple concept of "10 out of 24000," explaining how to interpret this ratio, how to express it in different forms, and how such calculations apply to various real-world scenarios. We'll explore the underlying mathematical principles and demonstrate their practical relevance, making the concept accessible and engaging for everyone.
Introduction: What Does 10 out of 24000 Mean?
The phrase "10 out of 24000" represents a ratio, a comparison of two numbers. It signifies that there are 10 instances of something within a larger population of 24000. This ratio can be used to describe various situations, such as the number of defective items in a batch of products, the percentage of students achieving a certain grade, or the occurrence of a specific event within a larger dataset. Understanding how to manipulate and interpret this ratio is crucial for drawing meaningful conclusions and making informed decisions. We'll explore different ways to represent this ratio and its implications.
Understanding Ratios and Proportions: A Mathematical Foundation
A ratio is a mathematical comparison between two quantities. It can be expressed in several ways:
- Using the word "to": 10 to 24000
- Using a colon: 10:24000
- As a fraction: 10/24000
A proportion is a statement that two ratios are equal. Proportions are incredibly useful for solving problems where we know a part and need to find the whole, or vice versa. We can use proportions to scale recipes, calculate percentages, and determine probabilities.
Simplifying the Ratio: Finding the Simplest Form
The ratio 10/24000 can be simplified by finding the greatest common divisor (GCD) of 10 and 24000. The GCD of 10 and 24000 is 10. Dividing both the numerator and the denominator by 10, we get:
10/24000 = 1/2400
This simplified form represents the same ratio but is easier to understand and work with. It means that for every 2400 items, one is of the specified type.
Expressing the Ratio as a Percentage:
To express the ratio as a percentage, we divide the numerator by the denominator and multiply by 100:
(1/2400) * 100 ≈ 0.04167%
This means that approximately 0.04167% of the total population (24000) represents the 10 instances.
Expressing the Ratio as a Decimal:
The decimal representation of the ratio is simply the result of the division:
1/2400 ≈ 0.0004167
This decimal form is often useful for calculations and comparisons.
Real-World Applications of Ratios and Proportions:
The concept of "10 out of 24000" can be applied to various real-world scenarios. Let's explore a few examples:
-
Quality Control: Imagine a factory producing 24000 light bulbs. If 10 bulbs are found to be defective during quality control, the ratio 10/24000 (or 1/2400) indicates the defect rate. This information helps determine the effectiveness of the manufacturing process and identify areas for improvement.
-
Statistical Analysis: In a survey of 24000 people, if 10 respondents answered "yes" to a specific question, the ratio 10/24000 helps determine the proportion of the population that holds that particular opinion. This is essential for understanding public sentiment or consumer preferences.
-
Environmental Studies: If 10 endangered birds are found in a population of 24000 birds of the same species, the ratio highlights the critical conservation status of the species and the need for intervention.
-
Medical Research: In a clinical trial with 24000 participants, if 10 experience a specific side effect from a drug, this ratio is crucial for evaluating the drug's safety profile and determining potential risks.
-
Financial Analysis: In a portfolio of 24000 stocks, if 10 underperform significantly, the ratio helps identify risk areas and inform investment strategies.
Solving Problems Using Proportions:
Proportions are invaluable tools for solving problems involving ratios. For example:
- Scaling Recipes: If a recipe calls for 10 grams of spice for 24000 grams of food, how much spice is needed for 6000 grams of food? We can set up a proportion:
10/24000 = x/6000
Solving for x, we find that 2.5 grams of spice are needed.
- Calculating Percentages: What percentage of 24000 is 10? We can use the ratio as a fraction and multiply by 100:
(10/24000) * 100 ≈ 0.04167%
Beyond the Basics: Exploring Advanced Concepts
While "10 out of 24000" is a straightforward ratio, understanding it opens the door to more complex concepts:
-
Sampling and Inference: In statistics, a small sample (like the 10 instances) can be used to make inferences about a larger population (the 24000). However, the accuracy of these inferences depends heavily on the sampling method and the size of the sample relative to the population.
-
Probability and Risk Assessment: The ratio can represent the probability of a certain event occurring. The lower the ratio (in this case, a very low probability), the lower the likelihood of the event. This is crucial in risk assessment and decision-making.
-
Data Analysis and Interpretation: Analyzing ratios like this is crucial in interpreting data and drawing meaningful conclusions. Understanding the context of the ratio (what the 10 and 24000 represent) is vital for accurate interpretation.
Frequently Asked Questions (FAQ):
-
How do I know which ratio form to use? The best form depends on the context. Percentages are easy to understand for general audiences, while fractions are useful for calculations, and decimals are often used in computer programs and spreadsheets.
-
Can I express this ratio differently? Yes, you can also express it as a rate (e.g., 10 occurrences per 24000 units) or as a proportion (e.g., 10 out of 24000 is equivalent to x out of y).
-
What if I have a larger or smaller number of instances? The same principles apply regardless of the numbers. You can still simplify the ratio, convert it to a percentage or decimal, and use it in proportions.
-
How do I handle very small or very large numbers? Scientific notation is helpful for working with extremely large or small numbers.
Conclusion: The Power of Understanding Ratios and Proportions
The seemingly simple ratio of "10 out of 24000" embodies fundamental mathematical concepts with far-reaching real-world applications. By understanding how to simplify, represent, and utilize ratios and proportions, we can gain valuable insights from data, make informed decisions, and solve problems across various disciplines. This understanding is not merely a mathematical skill; it's a crucial tool for navigating and interpreting the quantitative world around us. The ability to dissect and analyze ratios empowers us to understand data, make better judgments, and approach problem-solving with greater clarity and precision. Remember, mastering this fundamental concept is a stepping stone to more advanced mathematical and analytical skills, unlocking a deeper understanding of the world and empowering you to confidently tackle complex challenges.
Latest Posts
Latest Posts
-
Animal Farm Mollie
Sep 23, 2025
-
3 X 3 7
Sep 23, 2025
-
35 Sq Meters
Sep 23, 2025
-
Rats Collective Noun
Sep 23, 2025
-
Three Headed Snake
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 24000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.