3 X 3/7
interactiveleap
Sep 23, 2025 · 6 min read
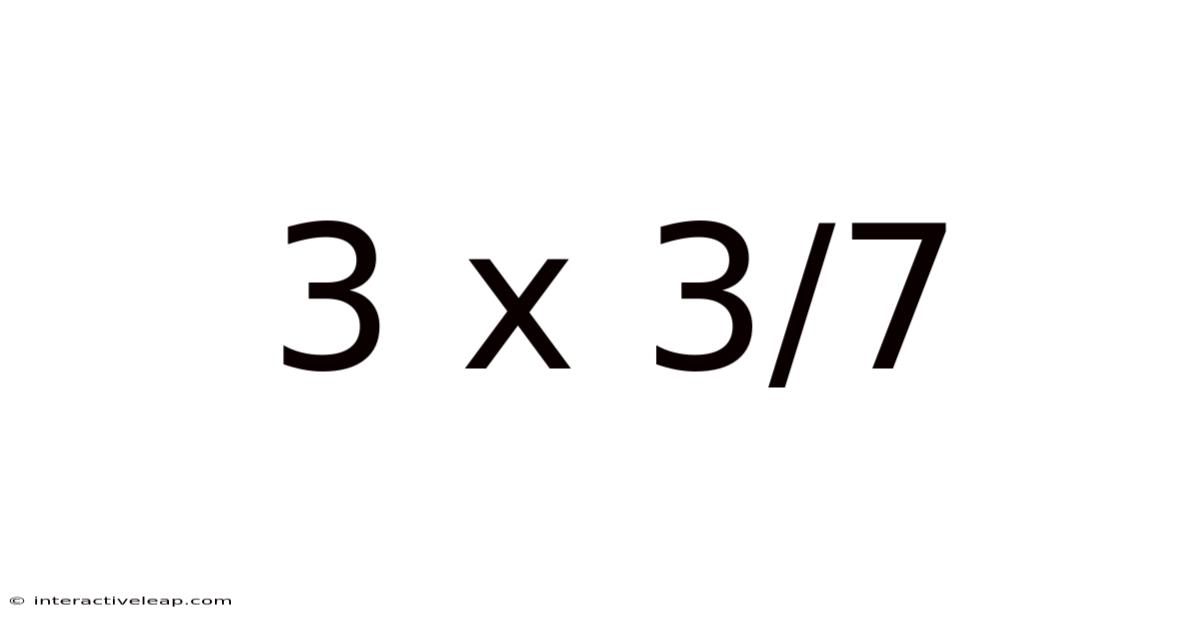
Table of Contents
Unveiling the Mystery: A Deep Dive into 3 x 3/7
Understanding fractions and how to multiply them can seem daunting at first, but with a clear approach and a bit of practice, it becomes second nature. This article will explore the seemingly simple calculation of 3 x 3/7, breaking it down step-by-step to reveal the underlying principles and expanding upon the broader concepts of fraction multiplication. We'll delve into the mathematical reasoning, offer practical examples, and address frequently asked questions, ensuring a comprehensive understanding for learners of all levels. By the end, you'll not only know the answer to 3 x 3/7 but also possess a solid foundation for tackling more complex fraction problems.
Understanding the Basics: Fractions and Multiplication
Before we tackle 3 x 3/7, let's refresh our understanding of fractions and their multiplication. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/7, 3 is the numerator and 7 is the denominator. This means we have 3 out of 7 equal parts of a whole.
Multiplying fractions involves multiplying the numerators together and the denominators together. For example:
(a/b) x (c/d) = (a x c) / (b x d)
This rule applies whether the fractions are simple or complex. It's crucial to remember that this process doesn't involve finding a common denominator like in addition or subtraction of fractions.
Solving 3 x 3/7: A Step-by-Step Approach
Now, let's apply this knowledge to our problem: 3 x 3/7. To solve this, we can represent the whole number 3 as a fraction: 3/1. This doesn't change its value, as any number divided by 1 remains the same.
Therefore, our problem becomes:
(3/1) x (3/7)
Following the rule for multiplying fractions:
- Multiply the numerators: 3 x 3 = 9
- Multiply the denominators: 1 x 7 = 7
This gives us the result: 9/7
This is an improper fraction because the numerator (9) is larger than the denominator (7). Improper fractions are perfectly valid mathematically, but it's often helpful to convert them into mixed numbers for better understanding.
Converting Improper Fractions to Mixed Numbers
A mixed number combines a whole number and a proper fraction. To convert 9/7 into a mixed number, we perform division:
9 ÷ 7 = 1 with a remainder of 2
This means that 9/7 is equivalent to 1 whole and 2/7. Therefore, the final answer to 3 x 3/7 is 1 2/7.
Visualizing the Problem: A Practical Approach
Visualizing the problem can enhance understanding. Imagine a pizza cut into 7 equal slices. 3 x 3/7 means we're taking three sets of 3/7 of the pizza. Each set comprises 3 slices. Taking three of these sets gives us 9 slices in total. Since the pizza has 7 slices, we have 1 whole pizza (7 slices) and 2 slices remaining, representing 1 2/7 pizzas.
Expanding on Fraction Multiplication: More Complex Scenarios
While 3 x 3/7 is a relatively straightforward example, let's examine more complex scenarios to solidify our understanding of fraction multiplication.
Scenario 1: Multiplying multiple fractions:
Consider the problem: (2/3) x (4/5) x (1/2).
Following the same principle, we multiply all the numerators together and all the denominators together:
(2 x 4 x 1) / (3 x 5 x 2) = 8/30
This fraction can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 2:
8/30 = 4/15
Scenario 2: Multiplying fractions with whole numbers and mixed numbers:
Let's tackle the problem: 2 1/2 x 3/4.
First, convert the mixed number 2 1/2 into an improper fraction:
2 1/2 = (2 x 2 + 1) / 2 = 5/2
Now, multiply the fractions:
(5/2) x (3/4) = 15/8
Converting the improper fraction 15/8 to a mixed number:
15 ÷ 8 = 1 with a remainder of 7
Therefore, 15/8 = 1 7/8
The Importance of Simplification
In many fraction problems, simplification is crucial. It makes the answer easier to understand and work with. Simplification involves dividing both the numerator and denominator by their greatest common divisor (GCD). For example, in the fraction 8/30, the GCD of 8 and 30 is 2. Dividing both by 2 simplifies the fraction to 4/15. Always simplify your answer whenever possible to present the most concise and accurate result.
Applications of Fraction Multiplication in Real Life
Fraction multiplication is not just a mathematical exercise; it has numerous real-world applications. Here are a few examples:
- Cooking and Baking: Recipes often require fractions of ingredients. If a recipe calls for 2/3 cup of flour and you want to double the recipe, you'll need to multiply 2/3 by 2.
- Construction and Engineering: Calculations involving measurements often involve fractions. Determining the amount of material needed for a project may require multiplying fractions.
- Finance: Calculating percentages, discounts, and interest often involves fraction multiplication.
- Data Analysis: Many statistical calculations utilize fractions and their multiplication.
Frequently Asked Questions (FAQ)
Q1: What if I have a negative number in the multiplication?
A1: The rules remain the same. Multiply the numbers as usual. If you have an odd number of negative numbers in the multiplication, the result will be negative. If you have an even number of negative numbers, the result will be positive.
Q2: Can I multiply fractions in any order?
A2: Yes, fraction multiplication is commutative. This means you can multiply fractions in any order, and the result will remain the same.
Q3: How do I deal with fractions containing zero?
A3: If the numerator is zero, the result is always zero (0/x = 0, where x is not zero). If the denominator is zero, the fraction is undefined.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is a cornerstone of mathematical proficiency. This article has provided a detailed explanation of how to solve 3 x 3/7, highlighting the underlying principles and demonstrating practical applications. By understanding the steps involved, from converting whole numbers to fractions to simplifying improper fractions, you can confidently approach more complex problems. Remember the key principles: multiply numerators, multiply denominators, and always simplify your final answer. With consistent practice and a clear understanding of the concepts, you'll be well on your way to mastering fractions and their diverse applications in the real world. Don't be afraid to revisit these steps and practice; the more you work with fractions, the easier they will become.
Latest Posts
Latest Posts
-
Write On Pencils
Sep 23, 2025
-
25 Of 41
Sep 23, 2025
-
Esd Wrist Wrap
Sep 23, 2025
-
10 Of 34
Sep 23, 2025
-
Asap Rockys Hair
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 3 X 3/7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.