10 Of 125.00
interactiveleap
Sep 22, 2025 · 6 min read
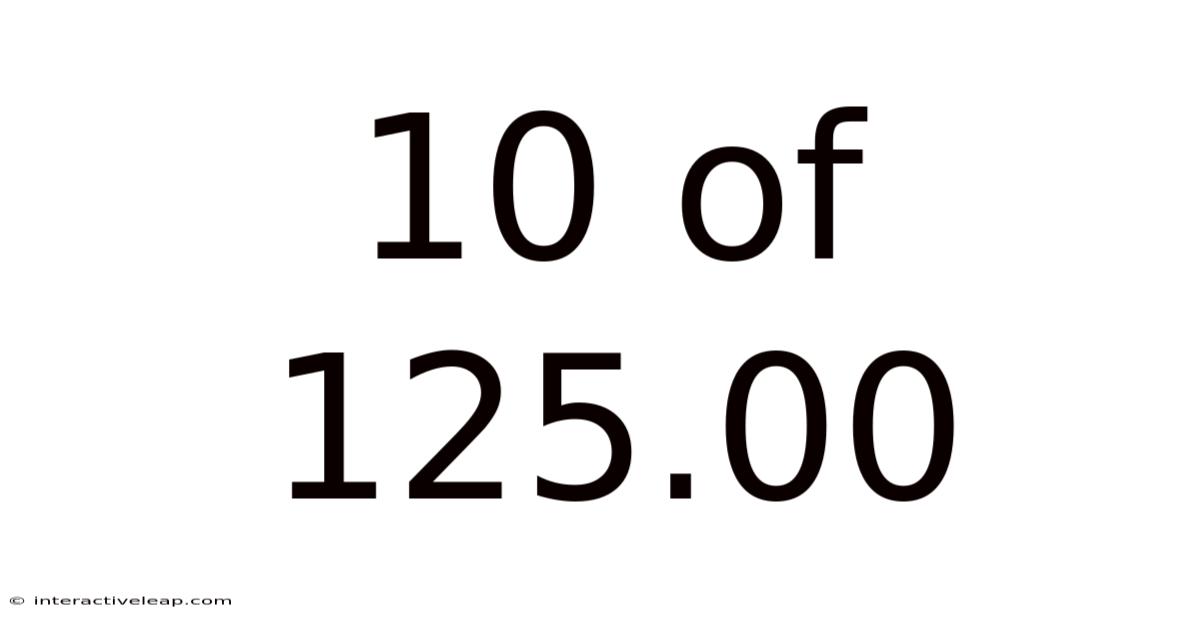
Table of Contents
Decoding 10 of 125.00: A Deep Dive into Fractions, Percentages, and Ratios
Understanding fractions, percentages, and ratios is fundamental to many aspects of life, from baking a cake to managing finances. This article will explore the meaning of "10 of 125.00," breaking down its representation in different mathematical forms and demonstrating its practical applications. We will delve into the calculations, explore the underlying concepts, and provide examples to solidify your understanding. This comprehensive guide is designed for anyone looking to improve their mathematical literacy, regardless of their prior experience.
Introduction: Understanding the Core Concept
The expression "10 of 125.00" represents a part-to-whole relationship. It signifies that we have 10 units out of a total of 125.00 units. This seemingly simple phrase opens the door to understanding several crucial mathematical concepts: fractions, percentages, and ratios. We'll dissect each of these representations to illuminate the various ways of interpreting this relationship.
1. Representing "10 of 125.00" as a Fraction
A fraction represents a part of a whole. In our case, the part is 10, and the whole is 125.00. Therefore, "10 of 125.00" can be written as the fraction 10/125. This fraction can be simplified by finding the greatest common divisor (GCD) of 10 and 125, which is 5. Dividing both the numerator (10) and the denominator (125) by 5, we get the simplified fraction 2/25.
- Key takeaway: The fraction 2/25 is equivalent to 10/125 and represents the same proportion. Simplifying fractions makes them easier to understand and work with.
2. Converting the Fraction to a Percentage
A percentage is a way of expressing a fraction as a portion of 100. To convert the fraction 2/25 to a percentage, we need to find an equivalent fraction with a denominator of 100. We can do this by multiplying both the numerator and the denominator by 4 (since 25 x 4 = 100):
(2 x 4) / (25 x 4) = 8/100
Therefore, 2/25 is equal to 8/100, which is represented as 8%.
Alternatively, you can directly convert the fraction to a percentage by dividing the numerator by the denominator and multiplying the result by 100:
(10 / 125) x 100 = 8%
- Key takeaway: 8% represents the proportion of 10 out of 125.00 as a percentage. Percentages provide a standardized way to compare proportions.
3. Expressing "10 of 125.00" as a Ratio
A ratio expresses the relationship between two or more quantities. In our case, the ratio is 10:125, which represents the relationship between the part (10) and the whole (125). Similar to the fraction, this ratio can be simplified by dividing both parts by their GCD (5):
10:125 simplifies to 2:25
This means that for every 2 units of one quantity, there are 25 units of the other quantity.
- Key takeaway: Ratios provide a concise way to compare two or more quantities. They are often used in situations where the relative sizes of the quantities are important.
4. Practical Applications: Real-World Examples
The concept of "10 of 125.00" has numerous practical applications in everyday life. Let's consider a few examples:
-
Inventory Management: If a store has 125 units of a particular product and 10 of them are sold, the fraction 10/125 (or 8%) represents the proportion of the inventory sold.
-
Test Scores: If a student answers 10 questions correctly out of a total of 125 questions on a test, their score is 8%.
-
Financial Analysis: If a company's total revenue is 125.00 units and 10 units are profit, then 8% represents the profit margin.
-
Survey Results: If 10 out of 125 respondents to a survey answered "yes" to a particular question, then 8% of the respondents gave a "yes" response.
-
Recipe Scaling: If a recipe calls for 125 grams of flour and you only want to use 10 grams, you're using 8% of the original recipe amount.
These examples demonstrate the versatility of understanding fractions, percentages, and ratios in different contexts.
5. Beyond the Basics: Exploring Further Concepts
While understanding the basic conversions between fractions, percentages, and ratios is crucial, let's delve into some more advanced concepts related to "10 of 125.00":
-
Proportional Reasoning: This involves understanding and applying the relationship between different parts of a whole. For example, if you know that 10 out of 125 represents 8%, you can use proportional reasoning to determine how many units would represent, say, 16% or 24%.
-
Inverse Proportion: If the number of units (10) remains constant, an increase in the total units (125) would result in a decrease in the percentage. Conversely, a decrease in the total units would lead to an increase in the percentage.
-
Percentage Increase/Decrease: Suppose the initial amount was 10 out of 125, and it increased to 15 out of 125. Calculating the percentage increase would involve determining the difference (5) and expressing it as a percentage of the original amount (10).
-
Compounding Percentages: Imagine that 8% of the 125 units were lost, and then another 8% of the remaining units were lost. Understanding compounding percentages helps calculate the overall loss accurately.
6. Frequently Asked Questions (FAQ)
-
Q: What is the difference between a fraction and a ratio?
- A: While both fractions and ratios express a part-to-whole relationship, fractions are typically used to represent a part of a whole, while ratios can compare any two or more quantities. A fraction always involves a single whole, while a ratio can involve multiple quantities.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand and compare. It also simplifies calculations involving fractions.
-
Q: How can I convert a decimal to a percentage?
- A: To convert a decimal to a percentage, multiply the decimal by 100 and add a percent sign (%). For instance, 0.08 is equivalent to 8%.
-
Q: How can I calculate percentage change?
- A: The percentage change is calculated by finding the difference between the new value and the original value, dividing the difference by the original value, and multiplying by 100%.
7. Conclusion: Mastering the Fundamentals
Understanding "10 of 125.00" and its various representations – as a fraction, percentage, and ratio – is crucial for navigating everyday situations. Mastering these concepts is not merely about memorizing formulas; it's about developing a deeper understanding of proportional reasoning and its applications across various fields. This article has explored the fundamental concepts, provided clear examples, and answered frequently asked questions, equipping you with the knowledge to confidently approach similar problems and apply these principles to real-world scenarios. Remember that consistent practice is key to mastering these essential mathematical skills. By continuing to work with fractions, percentages, and ratios, you will build a strong foundation for more advanced mathematical concepts. The ability to seamlessly translate between these forms enhances problem-solving abilities across various disciplines and contributes significantly to numeracy skills.
Latest Posts
Latest Posts
-
2 5 Of 500
Sep 22, 2025
-
5 6 18
Sep 22, 2025
-
2500 Times 12
Sep 22, 2025
-
4 Fingers Meme
Sep 22, 2025
-
343km To Mph
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 10 Of 125.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.