5 6 18
interactiveleap
Sep 22, 2025 · 6 min read
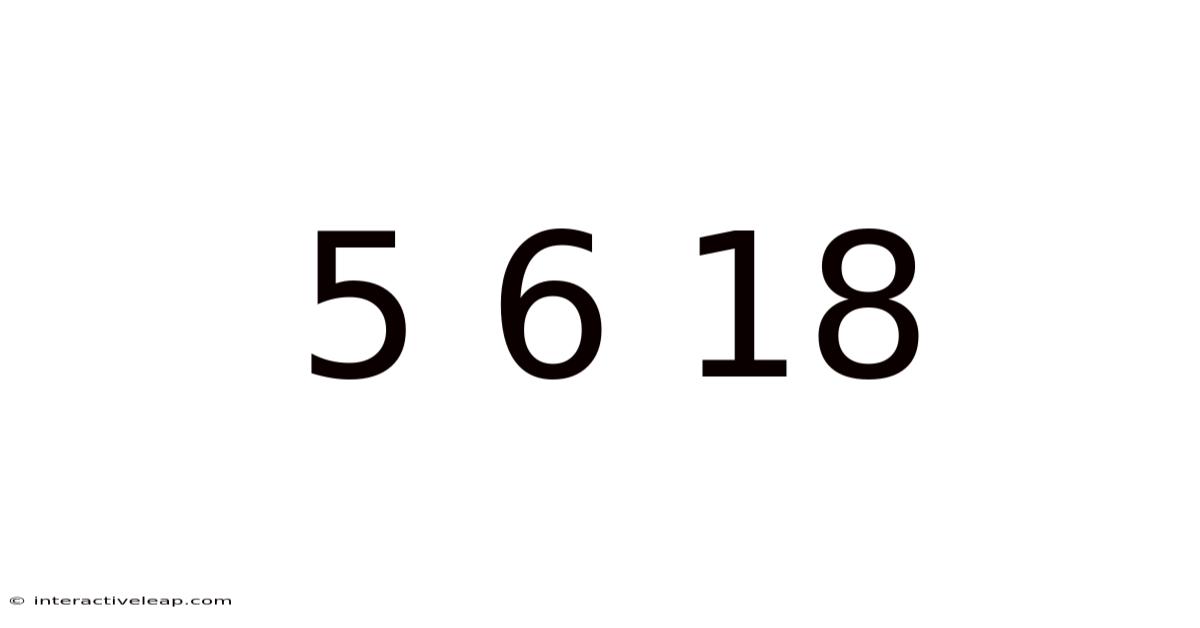
Table of Contents
Unraveling the Mystery: Exploring the Mathematical Relationships within 5, 6, and 18
The seemingly simple numbers 5, 6, and 18 hold a surprising depth of mathematical relationships. This exploration delves into their connections, revealing patterns and properties that extend beyond basic arithmetic. Understanding these relationships not only enhances mathematical comprehension but also demonstrates the interconnectedness of seemingly disparate numerical concepts. This article will unpack various aspects, from simple divisibility to more complex number theory concepts.
Introduction: A Foundation in Number Theory
At first glance, 5, 6, and 18 appear unrelated. However, a closer examination reveals a fascinating interplay of factors, multiples, and prime factorization. This investigation utilizes fundamental concepts of number theory, including prime numbers, divisibility rules, least common multiples (LCM), and greatest common divisors (GCD), to unveil the hidden connections between these three numbers. We'll explore their prime factorization, common factors and multiples, and examine their behavior within different mathematical contexts.
Prime Factorization: The Building Blocks
The cornerstone of understanding the relationships between 5, 6, and 18 lies in their prime factorization. Prime factorization involves expressing a number as the product of its prime factors – numbers divisible only by 1 and themselves.
-
5: 5 is a prime number itself. Its prime factorization is simply 5.
-
6: 6 is a composite number (not prime). Its prime factorization is 2 x 3.
-
18: 18 is also a composite number. Its prime factorization is 2 x 3 x 3, or 2 x 3².
This prime factorization immediately reveals some relationships. Both 6 and 18 share the prime factors 2 and 3, suggesting a connection based on divisibility. The number 5, being prime, stands apart, but its relationship to the others can be explored through multiples and other mathematical operations.
Divisibility and Factors: Exploring Common Ground
Understanding divisibility allows us to examine how these numbers relate to each other. Divisibility refers to whether one number can be divided by another without leaving a remainder.
- Factors of 6: The factors of 6 are 1, 2, 3, and 6.
- Factors of 18: The factors of 18 are 1, 2, 3, 6, 9, and 18.
- Factors of 5: The factors of 5 are 1 and 5.
Notice that 1, 2, 3, and 6 are common factors of both 6 and 18. This illustrates that 6 is a divisor of 18. However, 5 shares no common factors with 6 or 18 other than 1. This highlights the distinct nature of 5 compared to the other two numbers.
Multiples and Least Common Multiple (LCM): Expanding the Relationships
Multiples are the results of multiplying a number by integers. The least common multiple (LCM) is the smallest number that is a multiple of all the numbers in a set. Let's find the LCM of 5, 6, and 18.
To find the LCM, we can use the prime factorization method:
- List the prime factorizations: 5 = 5; 6 = 2 x 3; 18 = 2 x 3²
- Identify the highest power of each prime factor: The highest power of 2 is 2¹; the highest power of 3 is 3²; and the highest power of 5 is 5¹.
- Multiply the highest powers together: LCM(5, 6, 18) = 2 x 3² x 5 = 90
The LCM of 5, 6, and 18 is 90. This means that 90 is the smallest number divisible by all three numbers without leaving a remainder.
Greatest Common Divisor (GCD): Finding Common Ground
The greatest common divisor (GCD) is the largest number that divides all the numbers in a set without leaving a remainder. For 5, 6, and 18, we can use the Euclidean algorithm or prime factorization to find the GCD.
Using prime factorization:
- List the prime factorizations: 5 = 5; 6 = 2 x 3; 18 = 2 x 3²
- Identify common prime factors: There are no common prime factors among 5, 6, and 18 other than 1.
- Therefore, the GCD(5, 6, 18) = 1.
This indicates that 5, 6, and 18 are relatively prime; they share no common factors greater than 1.
Exploring Further Mathematical Relationships
Beyond basic divisibility and LCM/GCD, we can explore other mathematical connections:
-
Modular Arithmetic: Examining the remainders when these numbers are divided by various integers can reveal interesting patterns. For example, in modulo 3 arithmetic, 6 and 18 are congruent to 0 (meaning they are divisible by 3), while 5 is congruent to 2.
-
Number Sequences: While 5, 6, and 18 don't obviously form part of a known number sequence, they could serve as starting points for exploring patterns. For instance, one could explore sequences where the next term is derived using operations involving these three numbers.
-
Geometric Progressions: Although not directly a geometric progression, exploring the ratios between these numbers can lead to further mathematical investigation.
Applications and Real-World Examples
The concepts explored with 5, 6, and 18 are fundamental to numerous applications:
-
Scheduling and Timing: LCM is crucial in scheduling tasks that need to be synchronized. For example, if three machines operate with cycles of 5, 6, and 18 minutes, the LCM (90 minutes) determines when they will all simultaneously complete a cycle.
-
Resource Allocation: GCD is useful in dividing resources equally. If you have 18 apples and want to divide them equally among groups of 5 and 6 people, you must find the GCD to understand how many groups you can create without having any apples left over.
-
Cryptography: Prime factorization is a fundamental concept in modern cryptography, forming the basis of encryption algorithms. While 5, 6, and 18 themselves are not complex enough for cryptographic use, understanding prime factorization is key to appreciating the underlying principles.
Frequently Asked Questions (FAQ)
Q: Are 5, 6, and 18 part of any significant mathematical sequence?
A: While they don't directly belong to a widely recognized sequence like Fibonacci or arithmetic progressions, they can be used to generate various sequences depending on the chosen mathematical operations.
Q: What is the significance of the fact that their GCD is 1?
A: The fact that the GCD of 5, 6, and 18 is 1 signifies that they are relatively prime, meaning they share no common factors other than 1. This is a significant property in number theory and has implications in various applications, such as scheduling and resource allocation.
Q: Can these numbers be used to illustrate other mathematical concepts?
A: Absolutely. They can be used to demonstrate concepts like modular arithmetic, ratios, proportions, and the exploration of various number patterns and sequences. Their simplicity makes them ideal for introductory examples.
Conclusion: A Deeper Appreciation of Number Theory
The seemingly simple numbers 5, 6, and 18 offer a rich landscape for exploring fundamental concepts in number theory. Through the examination of prime factorization, divisibility, LCM, and GCD, we've uncovered their interconnectedness. This exploration not only illuminates the mathematical relationships between these specific numbers but also enhances our understanding of broader number theory principles. By understanding these basic concepts, we gain a deeper appreciation for the intricate and often hidden beauty within the world of mathematics, paving the way for further exploration of more complex mathematical ideas. The journey of uncovering these relationships highlights the interconnectedness of seemingly disparate mathematical concepts and encourages a deeper appreciation for the elegance and power of numbers.
Latest Posts
Latest Posts
-
Ealing Jazz Club
Sep 22, 2025
-
82 Degrees Fahrenheit
Sep 22, 2025
-
Breaking Bad Book
Sep 22, 2025
-
14 Cm Penisumfang
Sep 22, 2025
-
Break Even Song
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 5 6 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.