10/12 In Percentage
interactiveleap
Sep 22, 2025 · 5 min read
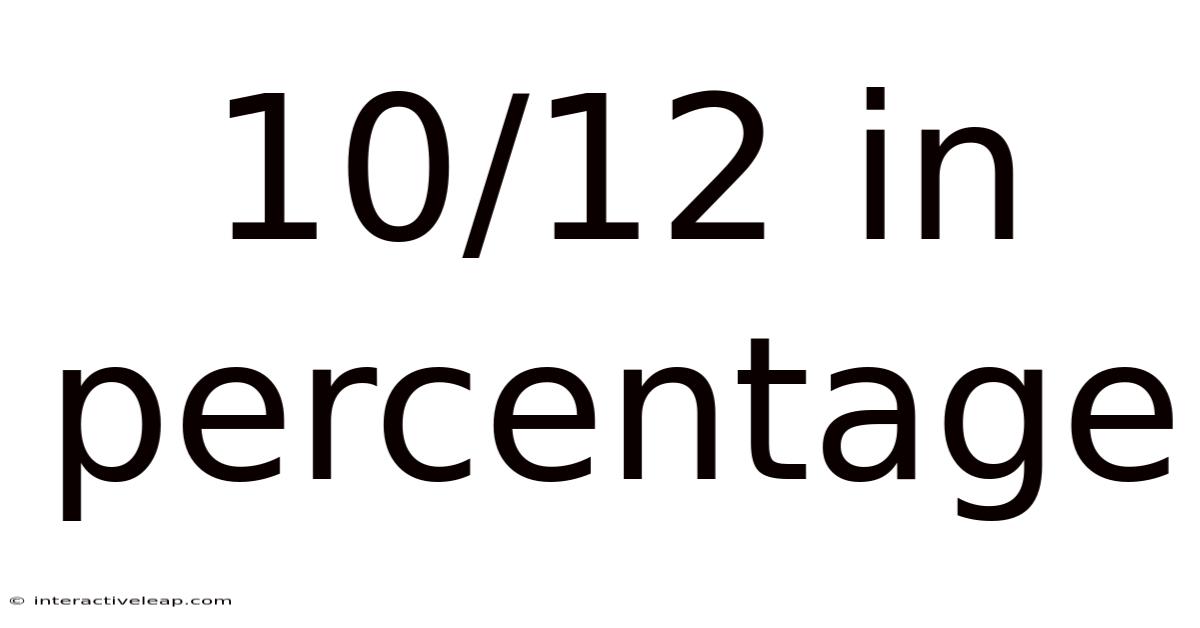
Table of Contents
Decoding 10/12 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts to understanding statistical data. This article will comprehensively explore how to convert the fraction 10/12 into a percentage, explaining the process step-by-step and delving into the underlying mathematical principles. We'll also explore different approaches to solving this problem and address frequently asked questions. By the end, you'll not only know the answer but also grasp the broader concept of fraction-to-percentage conversion.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In our case, the fraction is 10/12, where 10 is the numerator and 12 is the denominator.
A percentage, on the other hand, represents a fraction out of 100. The symbol "%" denotes percentage. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages provide a standardized way to compare and understand proportions.
Converting 10/12 to a Percentage: Step-by-Step
There are several ways to convert the fraction 10/12 into a percentage. Let's explore the most common and straightforward methods:
Method 1: Simplifying the Fraction and then Converting
This method involves simplifying the fraction to its lowest terms before converting it to a percentage. This often makes the calculation easier.
-
Simplify the Fraction: Both 10 and 12 are divisible by 2. Dividing both the numerator and the denominator by 2, we get:
10 ÷ 2 / 12 ÷ 2 = 5/6
-
Convert the Simplified Fraction to a Decimal: To convert a fraction to a decimal, divide the numerator by the denominator:
5 ÷ 6 ≈ 0.8333
-
Convert the Decimal to a Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.8333 x 100 ≈ 83.33%
Therefore, 10/12 is approximately equal to 83.33%.
Method 2: Direct Conversion to Percentage
This method involves directly converting the fraction to a percentage without simplifying it first.
-
Convert the Fraction to a Decimal: Divide the numerator (10) by the denominator (12):
10 ÷ 12 ≈ 0.8333
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the "%" symbol:
0.8333 x 100 ≈ 83.33%
As you can see, both methods yield the same result. The choice of method depends on personal preference and the complexity of the fraction. Simplifying first can sometimes make the calculation easier, especially with larger numbers.
Understanding the Result: 83.33%
The result, 83.33%, signifies that 10/12 represents 83.33 parts out of 100. This percentage can be interpreted in various contexts. For example, if you answered 10 out of 12 questions correctly on a test, your score would be approximately 83.33%.
Practical Applications of Percentage Calculations
The ability to convert fractions to percentages is crucial in various real-world scenarios:
- Academic Performance: Calculating grades, test scores, and overall academic progress.
- Financial Calculations: Determining discounts, interest rates, profit margins, and tax rates.
- Statistical Analysis: Representing data proportions and trends in charts and graphs.
- Everyday Life: Calculating tips, splitting bills, and understanding sales promotions.
Beyond the Basics: Working with More Complex Fractions
While 10/12 is a relatively simple fraction, the same principles apply to more complex fractions. The key steps remain the same:
- Simplify (if possible): Reduce the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator.
- Convert to Decimal: Divide the numerator by the denominator.
- Convert to Percentage: Multiply the decimal by 100 and add the "%" symbol.
For example, let's convert 25/40 to a percentage:
- Simplify: The GCD of 25 and 40 is 5. Dividing both by 5, we get 5/8.
- Convert to Decimal: 5 ÷ 8 = 0.625
- Convert to Percentage: 0.625 x 100 = 62.5%
Therefore, 25/40 is equal to 62.5%.
Frequently Asked Questions (FAQs)
Q1: Is 83.33% the exact percentage equivalent of 10/12?
A1: No, 83.33% is an approximation. The decimal representation of 5/6 (the simplified fraction) is a repeating decimal (0.8333...). To be completely accurate, we would write it as 83.333...%. However, for practical purposes, 83.33% is sufficiently accurate.
Q2: How can I perform these calculations without a calculator?
A2: For simpler fractions, you can often perform the division mentally or using long division. For more complex fractions, a calculator can be helpful, but understanding the underlying principles is crucial even when using a calculator.
Q3: What if the fraction is an improper fraction (numerator > denominator)?
A3: Improper fractions represent values greater than 1. Follow the same steps as above; the resulting percentage will be greater than 100%. For example, 12/10 simplifies to 6/5, which is 1.2, or 120%.
Q4: Are there other ways to express 10/12 as a ratio?
A4: Yes, 10/12 can be expressed as a ratio in various ways. The simplest is the simplified ratio 5:6, meaning 5 parts out of every 6 parts. You could also express it as 10:12, 20:24, 25:30, and so on; all these represent the same proportion.
Conclusion
Converting fractions to percentages is a valuable skill with far-reaching applications. We've explored multiple methods to convert 10/12 to its percentage equivalent (approximately 83.33%), emphasizing the importance of both understanding the underlying mathematical concepts and applying these skills in practical scenarios. By mastering these techniques, you'll be better equipped to navigate various mathematical problems in your academic and professional life. Remember, while calculators are helpful tools, understanding the process is crucial for developing a strong mathematical foundation.
Latest Posts
Latest Posts
-
Break Even Song
Sep 22, 2025
-
Long Subtraction Method
Sep 22, 2025
-
Supernatural Macbeth Quotes
Sep 22, 2025
-
2 Ethyl Butane
Sep 22, 2025
-
2 X 3x
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 10/12 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.