1/8 X 5
interactiveleap
Sep 21, 2025 · 6 min read
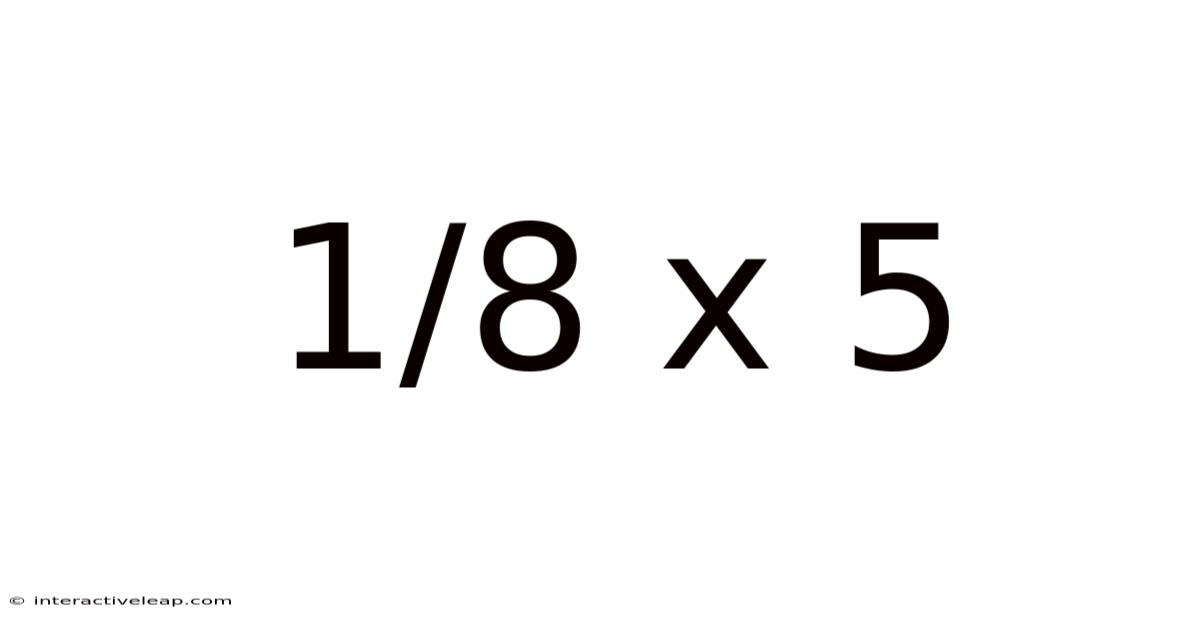
Table of Contents
Decoding 1/8 x 5: Exploring Fractions, Multiplication, and Real-World Applications
Understanding fractions and multiplication is fundamental to success in mathematics and numerous real-world applications. This comprehensive guide delves into the meaning of the expression "1/8 x 5," explaining the calculation process, exploring its practical implications, and addressing frequently asked questions. We'll break down the concept in an easy-to-understand manner, regardless of your current mathematical background. This guide will equip you with the tools to confidently tackle similar fractional multiplication problems.
Understanding the Basics: Fractions and Multiplication
Before tackling 1/8 x 5, let's review the fundamentals. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, 1/8 means one out of eight equal parts.
Multiplication, in its simplest form, is repeated addition. When we multiply a fraction by a whole number, we're essentially adding that fraction to itself the number of times indicated by the whole number. So, 1/8 x 5 means adding 1/8 to itself five times: 1/8 + 1/8 + 1/8 + 1/8 + 1/8.
Calculating 1/8 x 5: A Step-by-Step Approach
There are two primary methods for calculating 1/8 x 5:
Method 1: Repeated Addition
This method is visually intuitive, particularly for beginners. We simply add 1/8 to itself five times:
1/8 + 1/8 + 1/8 + 1/8 + 1/8 = 5/8
This demonstrates that five parts out of eight equal parts total 5/8.
Method 2: Multiplying the Numerator
A more efficient method involves multiplying the numerator of the fraction by the whole number:
1/8 x 5 = (1 x 5) / 8 = 5/8
This method directly gives us the result, 5/8, which represents five eighths. This approach is faster and more suitable for complex fractional calculations.
Visualizing 1/8 x 5: A Practical Example
Imagine a pizza cut into eight equal slices. 1/8 represents one slice. If you have five of these slices (1/8 x 5), you have 5/8 of the pizza. This visualization helps to solidify the understanding of the result: 5/8.
Real-World Applications of Fractional Multiplication
Fractional multiplication is prevalent in numerous everyday scenarios:
- Cooking and Baking: Recipes often require fractional measurements. For example, a recipe might call for 1/8 cup of sugar, and you need to multiply that amount by five to make a larger batch.
- Measurement and Construction: Construction projects often involve fractional measurements of inches or feet. Calculating the total length of multiple pieces requires fractional multiplication.
- Finance and Budgeting: Budgeting often involves working with fractions of money. For instance, calculating 1/8 of your monthly income for savings involves fractional multiplication.
- Data Analysis: In statistics and data analysis, fractional multiplication is frequently used for calculating proportions and percentages.
- Science and Engineering: Many scientific and engineering applications require precise calculations involving fractions, especially when dealing with measurements and proportions.
Expanding on the Concept: Multiplying Fractions by Fractions
While 1/8 x 5 involves multiplying a fraction by a whole number, let's briefly extend the concept to multiplying a fraction by another fraction. This builds upon the knowledge already gained.
To multiply two fractions, we multiply the numerators together and the denominators together. For example:
1/8 x 1/2 = (1 x 1) / (8 x 2) = 1/16
This means one-eighth of one-half is one-sixteenth. This concept is crucial for more advanced mathematical operations.
Simplifying Fractions: Reducing to Lowest Terms
Sometimes, the result of a fractional multiplication can be simplified. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).
Let's consider an example: 3/6. The GCD of 3 and 6 is 3. Dividing both the numerator and the denominator by 3 gives us 1/2. This means 3/6 is equivalent to 1/2.
While 5/8 (the result of 1/8 x 5) cannot be simplified further because 5 and 8 have no common divisor greater than 1, understanding simplification is essential for working with fractions effectively.
Converting Fractions to Decimals and Percentages
Fractions can be easily converted to decimals and percentages. To convert a fraction to a decimal, simply divide the numerator by the denominator:
5/8 = 5 ÷ 8 = 0.625
To convert a decimal to a percentage, multiply by 100:
0.625 x 100 = 62.5%
Therefore, 1/8 x 5 = 5/8 = 0.625 = 62.5%. This provides different ways to represent the same quantity, offering flexibility in various applications.
Frequently Asked Questions (FAQ)
Q1: What if I need to multiply 1/8 by a fraction instead of a whole number?
A1: To multiply two fractions, multiply the numerators together and then multiply the denominators together. For instance, 1/8 x 3/4 = (1 x 3) / (8 x 4) = 3/32.
Q2: How can I visualize multiplying fractions?
A2: Using diagrams, such as dividing a rectangle into equal parts, helps visualize fractions and their multiplication. For 1/8 x 5, you can represent a rectangle divided into eight parts and shade five of them.
Q3: Are there any online tools or calculators to help with fractional multiplication?
A3: While this guide aims to build conceptual understanding, many online calculators can perform fractional calculations. However, it's vital to grasp the underlying principles before relying heavily on such tools.
Q4: What if the result is an improper fraction (where the numerator is larger than the denominator)?
A4: An improper fraction can be converted to a mixed number, which consists of a whole number and a fraction. For example, 11/8 is an improper fraction; its equivalent mixed number is 1 3/8 (one and three-eighths).
Q5: How do I know if a fraction is in its simplest form?
A5: A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1. In other words, there's no number other than 1 that divides both the numerator and denominator evenly.
Conclusion:
Understanding fractional multiplication, exemplified by the calculation of 1/8 x 5, is a fundamental skill with wide-ranging applications. By mastering the techniques and understanding the underlying concepts, you can confidently tackle various problems involving fractions in diverse real-world contexts. Remember that practice is key; the more you work with fractions, the more comfortable and proficient you'll become. This guide provides a solid foundation for further exploration into the fascinating world of mathematics.
Latest Posts
Latest Posts
-
36 Of 125
Sep 21, 2025
-
140gms In Ounces
Sep 21, 2025
-
50 Of 40
Sep 21, 2025
-
Beatles Monopoly Board
Sep 21, 2025
-
Opposite Of Diligent
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 1/8 X 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.