1 3 10
interactiveleap
Sep 20, 2025 · 6 min read
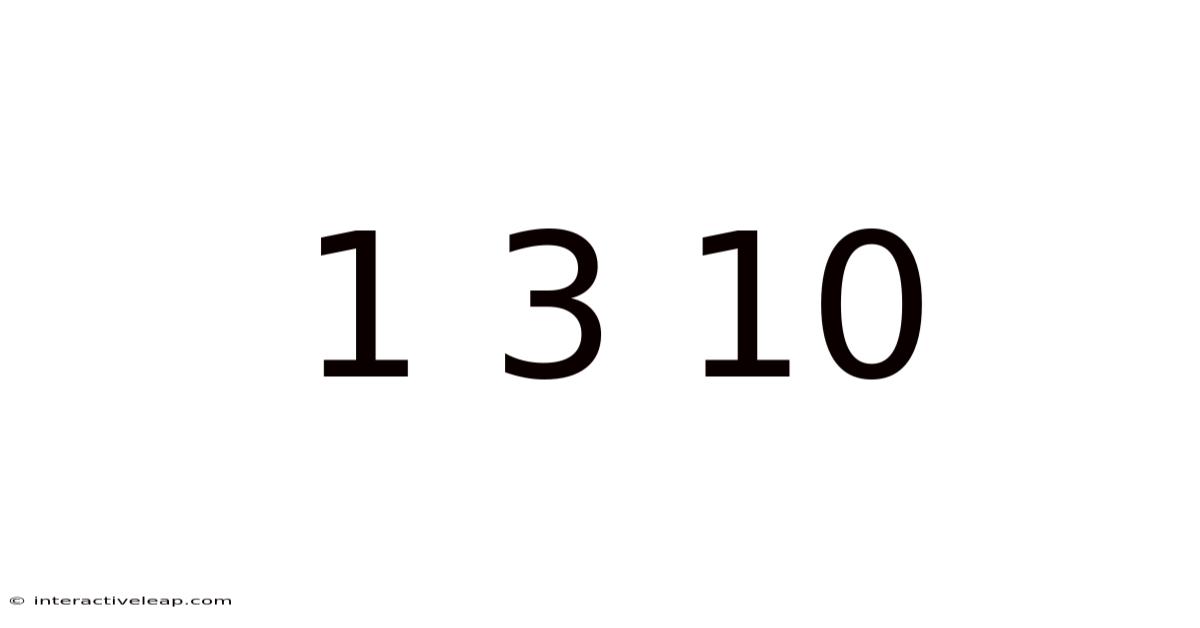
Table of Contents
Decoding the Mysterious Sequence: 1 3 10 – A Deep Dive into Pattern Recognition and Mathematical Exploration
The seemingly simple sequence "1 3 10" might appear innocuous at first glance. However, beneath its unassuming exterior lies a fascinating world of pattern recognition, mathematical exploration, and the inherent ambiguity of incomplete data. This article will delve deep into the possible interpretations of this sequence, exploring various mathematical approaches, discussing the importance of context, and ultimately highlighting the creative problem-solving skills required to unlock its secrets. Understanding this seemingly simple sequence can teach us valuable lessons about mathematical thinking and the importance of considering multiple perspectives.
Introduction: The Allure of the Unknown
The sequence 1, 3, 10 presents a classic puzzle. Without additional information or context, there's no single "correct" answer. This ambiguity is precisely what makes it so engaging. It encourages us to think critically, explore different possibilities, and develop our pattern recognition skills. This isn't just about finding an answer; it's about understanding how to find potential answers and evaluating their validity. We will explore several plausible patterns that could generate this sequence, demonstrating the diverse and often surprising ways mathematics can unravel seemingly random data.
Method 1: The Polynomial Approach
One common approach to deciphering numerical sequences is to fit them to a polynomial function. This involves finding a polynomial equation whose first few terms match the given sequence. For the sequence 1, 3, 10, we could use a quadratic equation of the form: an² + bn + c. Substituting the values from the sequence, we get the following system of equations:
- a(1)² + b(1) + c = 1
- a(2)² + b(2) + c = 3
- a(3)² + b(3) + c = 10
Solving this system of equations (using techniques like substitution or elimination) yields a specific solution for a, b, and c. While the exact solution will require algebraic manipulation, the principle is clear: We find a polynomial that generates the sequence. This method provides a formula that can be used to predict subsequent numbers in the sequence. However, it’s crucial to remember that this is just one possible interpretation; other polynomials could also fit the initial three numbers. This highlights the limitations of relying solely on polynomial fitting without additional context or data points.
Method 2: Recursive Relationships
Instead of a direct formula, we could explore recursive relationships. A recursive sequence defines each term based on the preceding terms. Let's consider some possibilities:
-
Option A: We could postulate a relationship where each term is obtained by adding an increasing value to the previous term. For example:
- 1 + 2 = 3
- 3 + 7 = 10 This suggests a pattern where the added values increase (2, 7, etc.). However, determining the rule governing this increase requires further data points.
-
Option B: A more complex recursive relationship could involve multiplying the previous term by a factor and then adding a constant. Or, even more complex relationships could involve using two or more previous terms to calculate the next one. The possibilities are vast.
The key takeaway is that recursive relationships offer a different approach, focusing on the interdependencies between terms rather than a direct formula. Again, without more information, several recursive rules could potentially generate the 1, 3, 10 sequence, leading to different predictions for subsequent terms.
Method 3: Geometric Series with Modification
While not a perfect fit, we could attempt to relate the sequence to a modified geometric series. A standard geometric series has a constant ratio between consecutive terms. This isn't directly apparent in 1, 3, 10. However, we might consider modifying a geometric series to create the sequence. For example, a series might begin with a geometric progression but then have a constant added or subtracted in each term. Exploring different modifications to geometric progressions, while unlikely to produce an exact match without further terms, provides another avenue for analytical exploration.
Method 4: Considering Context and External Factors
The most crucial point is the potential impact of context. The sequence "1 3 10" lacks intrinsic meaning. Its significance depends entirely on its origin. Where did this sequence come from?
- Is it a fragment of a larger sequence? If we had more numbers, it would be much easier to identify a pattern.
- Does it represent physical quantities? Perhaps these numbers represent measurements, coordinates, or other real-world data.
- Is it related to a specific mathematical concept? Could it be connected to a specific theorem, formula, or mathematical structure?
The lack of context renders any pattern purely speculative. The elegance of mathematics lies in its ability to model and explain the real world. Without a real-world connection, the sequence remains an abstract puzzle, open to multiple interpretations.
The Importance of Additional Data
The limitations of analyzing a short sequence like 1, 3, 10 highlight the critical role of sufficient data in pattern recognition and mathematical modeling. With only three numbers, an almost infinite number of patterns could be constructed. A longer sequence would considerably constrain the possibilities and allow for a more confident identification of the underlying rule or pattern.
Further Exploration and Advanced Techniques
For those interested in further exploration, more advanced mathematical techniques can be applied. These might include:
- Difference Tables: Analyzing the differences between consecutive terms can reveal patterns that might not be immediately apparent.
- Generating Functions: Generating functions provide a powerful algebraic tool for studying sequences.
- Recurrence Relations: More sophisticated recurrence relations can model intricate relationships between terms.
These techniques require a deeper understanding of mathematical concepts, but they offer more powerful tools for analyzing sequences.
Conclusion: Embracing the Ambiguity
The sequence 1, 3, 10 serves as a valuable illustration of the inherent ambiguity in incomplete data. There is no single "right" answer; multiple plausible patterns can be constructed. The exercise, however, is not about finding a definitive solution but about developing critical thinking skills, exploring different analytical approaches, and understanding the limitations of limited information. This puzzle highlights the importance of context, the power of mathematical modeling, and the continuous refinement of our understanding as more data becomes available. It showcases the beauty of mathematics not only in providing definitive answers but also in encouraging creative exploration and problem-solving. The journey of exploring this sequence is far more valuable than reaching a specific numerical conclusion. It’s a testament to the open-ended nature of mathematical inquiry and the importance of questioning, exploring, and refining our understanding in the face of uncertainty. This simple sequence, therefore, acts as a microcosm of the larger scientific process, reminding us that the search for knowledge is often as important as the discovery itself.
Latest Posts
Latest Posts
-
Average Potato Weight
Sep 21, 2025
-
X 15 9
Sep 21, 2025
-
Burgundy Blue Color
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 1 3 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.