1.25 X 3
interactiveleap
Sep 20, 2025 · 5 min read
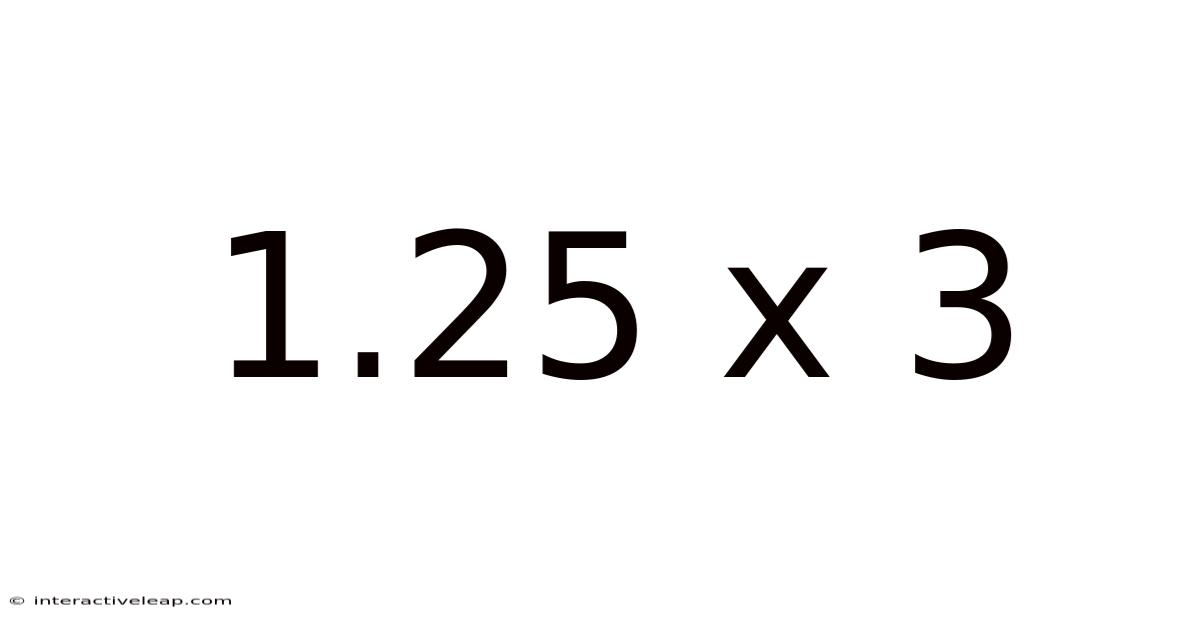
Table of Contents
Decoding 1.25 x 3: Exploring Multiplication and its Applications
This article delves into the seemingly simple mathematical equation, 1.25 x 3, exploring its solution, the underlying principles of decimal multiplication, and its practical applications across various fields. Understanding this seemingly basic calculation unlocks a deeper appreciation for mathematical foundations and their real-world relevance. We'll journey from the elementary steps to more advanced concepts, making this topic accessible to all readers, regardless of their mathematical background.
Introduction: Beyond the Basics of Multiplication
At first glance, 1.25 x 3 might appear trivial. It's a simple multiplication problem involving a decimal number. However, this seemingly straightforward calculation provides a springboard for exploring fundamental concepts in arithmetic and their broader implications. This article will not only solve the equation but also unpack the methodology, providing a solid understanding of working with decimals and demonstrating its relevance beyond the classroom. We'll uncover the "why" behind the "how," making this learning experience both informative and engaging.
Step-by-Step Calculation of 1.25 x 3
There are several ways to approach this multiplication problem. Let's explore the most common methods:
Method 1: Traditional Multiplication
This method involves treating the decimal as a whole number during the initial multiplication step and then adjusting the decimal point in the final answer.
-
Ignore the decimal point: Multiply 125 x 3.
- 125
- x 3
-
- 375
-
Adjust the decimal point: Since 1.25 has two decimal places, move the decimal point in the answer (375) two places to the left. This gives us the final answer: 3.75
Method 2: Fraction Conversion
Decimals can be expressed as fractions. This method involves converting the decimal to a fraction before performing the multiplication.
-
Convert the decimal to a fraction: 1.25 can be written as 125/100 (or simplified to 5/4).
-
Perform the multiplication: (5/4) x 3 = 15/4
-
Convert the fraction back to a decimal: 15/4 = 3.75
Method 3: Distributive Property
The distributive property allows us to break down the multiplication into smaller, manageable parts.
-
Break down 1.25: 1.25 can be written as 1 + 0.25
-
Apply the distributive property: (1 + 0.25) x 3 = (1 x 3) + (0.25 x 3) = 3 + 0.75 = 3.75
Each method yields the same result: 3.75
Understanding Decimal Multiplication: A Deeper Dive
The core concept behind decimal multiplication lies in understanding place value. Each digit in a number represents a specific power of 10. For instance, in the number 1.25:
- 1 represents 1 x 10⁰ (or 1)
- 2 represents 2 x 10⁻¹ (or 0.2)
- 5 represents 5 x 10⁻² (or 0.05)
When we multiply decimals, we're essentially multiplying these powers of 10. The placement of the decimal point in the final answer reflects the combined effect of these powers. The number of decimal places in the final product is the sum of the decimal places in the numbers being multiplied.
Real-World Applications of Decimal Multiplication
The seemingly simple calculation 1.25 x 3 has numerous applications in everyday life and various professional fields:
- Finance: Calculating the total cost of 3 items priced at $1.25 each. This is a straightforward application encountered frequently in daily shopping.
- Measurement: If a piece of wood is 1.25 meters long, and you need 3 such pieces, the total length required is 1.25 x 3 = 3.75 meters. This is important in carpentry, construction, and other fields involving precise measurements.
- Cooking and Baking: Many recipes involve fractional or decimal measurements of ingredients. Scaling a recipe up or down requires decimal multiplication. For instance, if a recipe calls for 1.25 cups of flour, and you want to triple the recipe, you'll need 1.25 x 3 = 3.75 cups of flour.
- Science and Engineering: Calculations involving scientific measurements often require working with decimals. This equation's principles extend to more complex scientific computations. Think of scenarios involving chemical concentrations, physical dimensions, or data analysis.
- Economics: Analyzing economic data often requires working with percentages and decimal representations of values. Understanding the underlying principles allows for accurate calculations and interpretations.
- Data Analysis: Statistical analysis often uses decimal numbers representing proportions, probabilities, or other data points. Multiplying these numbers is a fundamental aspect of analyzing and interpreting results.
Beyond 1.25 x 3: Extending the Concept
The principles demonstrated here extend to all decimal multiplication problems. The key takeaway is to understand the underlying principles of place value and decimal representation. This understanding empowers you to tackle more complex calculations involving larger numbers and multiple decimal places with confidence.
Frequently Asked Questions (FAQ)
-
What if one of the numbers is a whole number? The process remains the same. Treat the whole number as having zero decimal places, and the number of decimal places in the final answer will be equal to the number of decimal places in the decimal number. For example, 5 x 1.25 = 6.25 (two decimal places).
-
What if I have more than one decimal number? Add the total number of decimal places in all numbers being multiplied. The resulting answer will have that many decimal places. For example, 1.25 x 2.5 = 3.125 (three decimal places).
-
How can I check my answer? You can use a calculator to verify your answer, or you can reverse the process using division. If 1.25 x 3 = 3.75, then 3.75 / 3 should equal 1.25.
-
Are there other methods for solving decimal multiplication problems? Yes, there are various other approaches, including using long multiplication with decimals, and leveraging mathematical properties like the associative and commutative properties.
Conclusion: Mastering the Fundamentals
The seemingly simple equation, 1.25 x 3, provides a valuable window into the world of decimal multiplication. By understanding the step-by-step process, the underlying principles of place value, and the diverse applications of this fundamental mathematical concept, you enhance your mathematical proficiency and your ability to tackle real-world challenges. From daily finances to scientific calculations, the power of understanding decimal multiplication extends far beyond the confines of the classroom. Embrace this knowledge, and you'll find yourself better equipped to navigate the quantitative aspects of life. The key is consistent practice and a deeper understanding of the "why" behind the mathematical processes.
Latest Posts
Latest Posts
-
2 5 Of 25000
Sep 20, 2025
-
40l To Gallons
Sep 20, 2025
-
1 4 9
Sep 20, 2025
-
30 Of 57
Sep 20, 2025
-
25 Square Meters
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1.25 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.