1.2 X 60
interactiveleap
Sep 15, 2025 · 5 min read
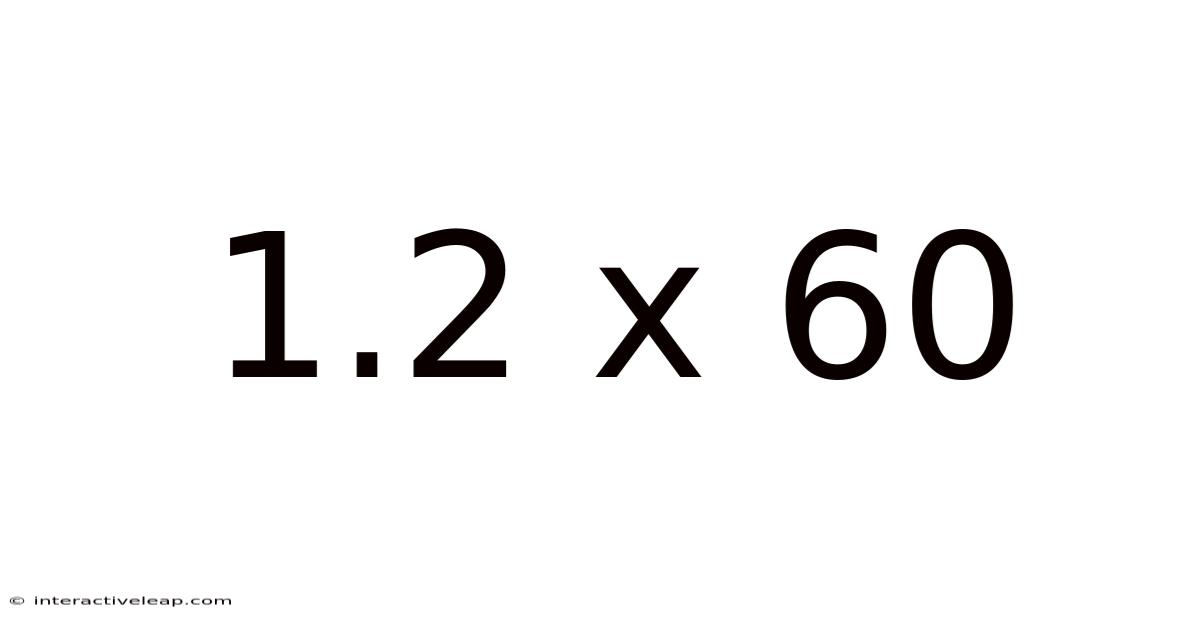
Table of Contents
Decoding 1.2 x 60: Exploring the Multiplicative Relationship and its Applications
This article delves into the seemingly simple mathematical expression "1.2 x 60," exploring its calculation, real-world applications across various fields, and the underlying concepts of decimal multiplication. We'll uncover the significance of understanding this calculation, not just for achieving the numerical answer, but for grasping the broader implications in practical problem-solving. By the end, you will not only know the result but also understand the process and its diverse uses.
Understanding the Fundamentals: Decimal Multiplication
Before diving into the specific calculation, let's refresh our understanding of decimal multiplication. Multiplying decimals involves the same basic principles as multiplying whole numbers, but with an added step: handling the decimal point. The key is to initially ignore the decimal points, multiply the numbers as if they were whole numbers, and then place the decimal point in the final answer based on the total number of decimal places in the original numbers.
For example, in the expression 1.2 x 60, we have one decimal place in 1.2 (the "2" after the decimal point). The number 60 has no decimal places. Therefore, the final answer will have one decimal place.
Calculating 1.2 x 60
Now let's tackle the calculation: 1.2 x 60.
There are several ways to approach this:
- Standard Multiplication: We can perform standard multiplication as follows:
1.2
x 60
-------
00
720
-------
72.0
Therefore, 1.2 x 60 = 72.
- Breaking Down the Calculation: We can also break down the calculation into simpler steps:
1.2 x 60 can be rewritten as (1 + 0.2) x 60. This allows us to calculate:
- 1 x 60 = 60
- 0.2 x 60 = 12
Adding these results together: 60 + 12 = 72
- Using Fractions: We can convert 1.2 to a fraction: 1.2 = 12/10 = 6/5. Then, the calculation becomes:
(6/5) x 60 = (6 x 60) / 5 = 360 / 5 = 72
All three methods arrive at the same answer: 72.
Real-World Applications of 1.2 x 60
The seemingly simple calculation of 1.2 x 60 has surprisingly diverse applications across numerous fields. Let's explore some examples:
-
Finance and Economics: Imagine calculating the total cost of 60 items priced at $1.20 each. The calculation 1.2 x 60 directly gives you the answer: $72. This simple multiplication is fundamental in inventory management, sales calculations, and various financial analyses. Similarly, understanding percentage increases (120% of 60) utilizes this principle.
-
Measurement and Conversion: In many engineering and scientific contexts, you might encounter conversions involving decimal multipliers. For instance, if you have a measurement of 60 units and need to increase it by 20%, the calculation would involve 1.2 x 60. This is crucial in fields like construction, manufacturing, and even recipe scaling in cooking.
-
Data Analysis and Statistics: In statistics, scaling data or calculating weighted averages might require similar multiplications. Imagine a scenario where you are analyzing survey data, where each response has a weight of 1.2 and you have 60 responses; the total weighted score would be 72.
-
Physics and Engineering: Many physical equations and engineering calculations involve multiplying decimals and whole numbers. Understanding 1.2 x 60, and similar calculations, provides a foundational understanding necessary for more complex calculations. For example, calculations related to force, acceleration, or energy might require similar manipulations.
Expanding the Concept: Beyond 1.2 x 60
The calculation 1.2 x 60 is a microcosm of broader mathematical concepts. Understanding its application allows for easier comprehension of:
-
Percentage Increases: Multiplying by 1.2 is equivalent to a 20% increase. This understanding can be extrapolated to other percentage increases or decreases.
-
Scaling and Proportionality: The calculation demonstrates the concept of scaling – increasing or decreasing a quantity proportionally. This is applicable in various contexts, from resizing images to adjusting recipes.
-
Linear Relationships: The calculation represents a simple linear relationship between two variables. This is a fundamental concept in algebra and its applications in modelling real-world phenomena.
Frequently Asked Questions (FAQ)
-
What if the numbers were different? The same principles apply to any similar calculation involving decimal multiplication. The method of breaking down the calculation, using fractions, or standard multiplication remains consistent.
-
How can I improve my speed in performing these calculations? Practice is key! Regularly working through similar problems and familiarizing yourself with different calculation methods will significantly enhance your speed and accuracy.
-
Are there any online tools or calculators to help? Numerous online calculators and mathematical tools are readily available to assist in decimal multiplication. However, understanding the underlying principles is crucial for developing problem-solving skills.
-
Why is understanding decimal multiplication important? Decimal multiplication is a fundamental skill applicable across numerous disciplines. Mastery of this concept forms the basis for tackling more complex mathematical problems in various fields, such as finance, engineering, and data science.
Conclusion: The Importance of Foundational Math
The calculation 1.2 x 60, while seemingly simple, exemplifies the importance of understanding fundamental mathematical concepts. Its applications extend far beyond a single numerical answer, providing a foundational understanding for problem-solving in various fields. Mastering decimal multiplication and the associated principles of scaling, proportionality, and linear relationships is crucial for anyone looking to excel in quantitative fields and for navigating the numerical challenges of everyday life. By understanding the why behind the calculation, we move beyond simply finding the answer (72) and unlock a deeper appreciation for the practical applications of mathematics. This understanding fosters confidence and opens doors to tackling more complex mathematical problems with greater ease and efficiency.
Latest Posts
Latest Posts
-
90 In Feet
Sep 15, 2025
-
800mm In Inches
Sep 15, 2025
-
Density Of Cu
Sep 15, 2025
-
95 Of 180
Sep 15, 2025
-
28 Of 650
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 1.2 X 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.