95 Of 180
interactiveleap
Sep 15, 2025 · 5 min read
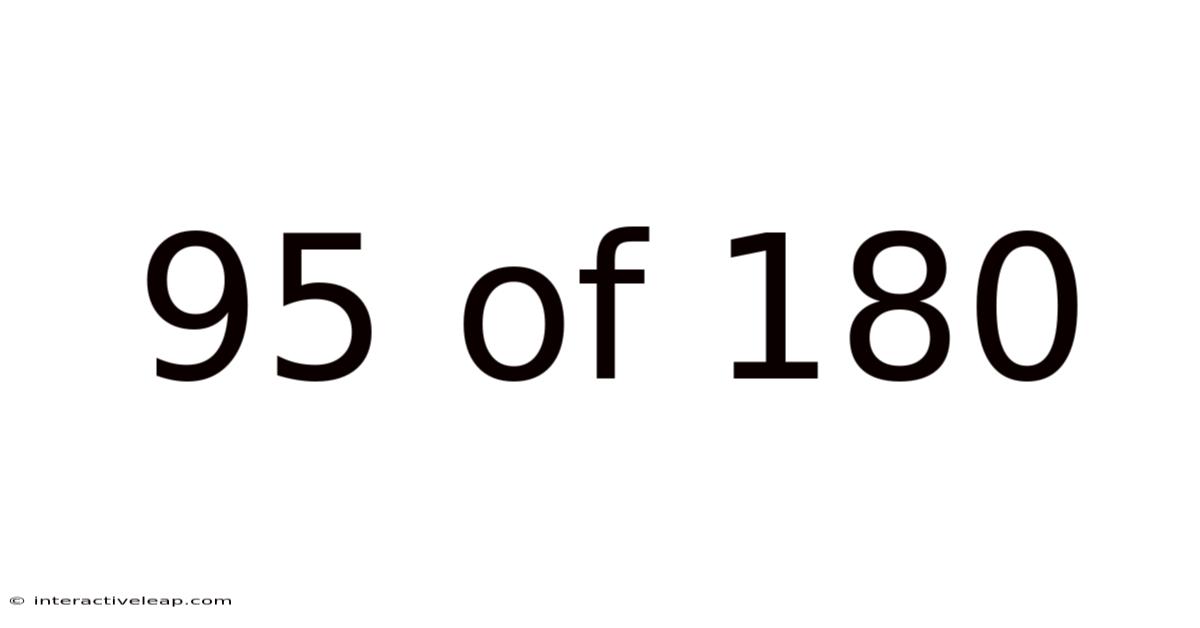
Table of Contents
Decoding the Fraction 95/180: A Comprehensive Guide to Simplification, Applications, and Understanding Ratios
Understanding fractions is fundamental to grasping mathematical concepts, from basic arithmetic to advanced calculus. This article delves into the fraction 95/180, exploring its simplification, practical applications, and the broader concept of ratios. We'll unpack the process of reducing fractions to their simplest form, demonstrating how to apply this knowledge in real-world scenarios, and addressing common questions about fractions. By the end, you'll have a solid understanding of 95/180 and a strengthened foundation in fractional arithmetic.
Introduction: What is 95/180?
The fraction 95/180 represents a part of a whole. The number 95 is the numerator, indicating the number of parts we have, while 180 is the denominator, representing the total number of equal parts that make up the whole. This fraction can be interpreted in various contexts, from dividing a pizza among friends to calculating proportions in scientific experiments. Our primary focus will be on simplifying this fraction and understanding its implications.
Simplifying 95/180: Finding the Greatest Common Divisor (GCD)
Before we delve into applications, simplifying 95/180 is crucial. Simplifying, also known as reducing a fraction, means finding an equivalent fraction with a smaller numerator and denominator. This is achieved by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both 95 and 180 without leaving a remainder.
To find the GCD, we can use several methods:
-
Listing Factors: List all the factors of 95 and 180. The largest factor common to both lists is the GCD.
- Factors of 95: 1, 5, 19, 95
- Factors of 180: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180
- The largest common factor is 5.
-
Prime Factorization: Break down both numbers into their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
- 95 = 5 x 19
- 180 = 2² x 3² x 5
- The common prime factor is 5 (with the lowest power of 1). Therefore, the GCD is 5.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. Repeatedly divide the larger number by the smaller number and replace the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
Now that we know the GCD is 5, we can simplify 95/180:
95 ÷ 5 = 19 180 ÷ 5 = 36
Therefore, the simplified fraction is 19/36. This fraction is in its simplest form because 19 and 36 share no common factors other than 1.
Practical Applications of 95/180 and its Simplified Form 19/36
The fraction 95/180, and its simplified equivalent 19/36, can be applied in numerous real-world situations:
-
Proportions and Percentages: Imagine you have a survey with 180 respondents, and 95 answered "yes" to a particular question. The fraction 95/180 (or 19/36) represents the proportion of "yes" responses. To calculate the percentage, we can divide 19 by 36 and multiply by 100: (19/36) * 100 ≈ 52.78%. Approximately 52.78% of respondents answered "yes."
-
Recipe Scaling: If a recipe calls for 95 grams of flour and 180 grams of sugar, the ratio of flour to sugar is 95:180, which simplifies to 19:36. You can use this simplified ratio to scale the recipe up or down. For example, to halve the recipe, you would use 9.5 grams of flour and 18 grams of sugar (halving both 19 and 36).
-
Geometry and Measurement: Consider a rectangle with a length of 180 cm and a width of 95 cm. The ratio of the width to the length is 95:180, simplifying to 19:36. This ratio helps understand the proportions of the rectangle.
-
Probability: If there are 180 equally likely outcomes in an experiment, and 95 of them correspond to a specific event, the probability of that event occurring is 95/180, or 19/36.
Converting Fractions to Decimals and Percentages
Understanding the decimal and percentage equivalents of 95/180 (or 19/36) provides further insight:
-
Decimal: To convert 19/36 to a decimal, divide 19 by 36: 19 ÷ 36 ≈ 0.5278
-
Percentage: To express this as a percentage, multiply the decimal by 100: 0.5278 * 100 ≈ 52.78%
Further Exploration: Working with Fractions
Beyond simplifying and converting, let's look at other operations involving fractions:
-
Addition and Subtraction: To add or subtract fractions, they must have a common denominator. For example, adding 19/36 and another fraction would require finding a common denominator before performing the operation.
-
Multiplication: Multiplying fractions is straightforward: multiply the numerators together and the denominators together. (19/36) * (x/y) = (19x)/(36y)
-
Division: Dividing fractions involves inverting the second fraction and multiplying. (19/36) ÷ (x/y) = (19/36) * (y/x) = (19y)/(36x)
Frequently Asked Questions (FAQ)
Q: What are some common mistakes people make when simplifying fractions?
A: A common mistake is not finding the greatest common divisor. Dividing by a common factor, but not the largest one, will result in a simplified fraction that is not in its simplest form. Another mistake is incorrectly dividing the numerator and denominator by different numbers.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand and work with. It allows for clearer comparisons and calculations, particularly in more complex mathematical operations. It also provides a more concise and efficient representation of the fraction.
Q: Are there any online tools or calculators to help simplify fractions?
A: Yes, many online calculators and tools can simplify fractions. Simply input the numerator and denominator, and the tool will provide the simplified form. However, understanding the underlying mathematical principles is crucial for building strong mathematical skills.
Conclusion: Mastering Fractions, One Step at a Time
Understanding fractions like 95/180 is crucial for building a robust foundation in mathematics. By learning to simplify fractions, calculate percentages and decimals, and apply these concepts to real-world problems, you'll enhance your numerical literacy significantly. Remember that practice is key. The more you work with fractions, the more comfortable and proficient you'll become. From understanding simple ratios to tackling more complex mathematical concepts, a solid grasp of fractions is indispensable. Don't hesitate to practice simplifying different fractions and applying them in various contexts. Mastering this fundamental concept opens up a world of mathematical possibilities.
Latest Posts
Latest Posts
-
1 25kg In Grams
Sep 15, 2025
-
Crossword Clue Sarcastic
Sep 15, 2025
-
Angry Crossword Clue
Sep 15, 2025
-
Art Of Cartooning
Sep 15, 2025
-
46 8kg In Stone
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 95 Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.