0.5 X 6
interactiveleap
Sep 22, 2025 · 6 min read
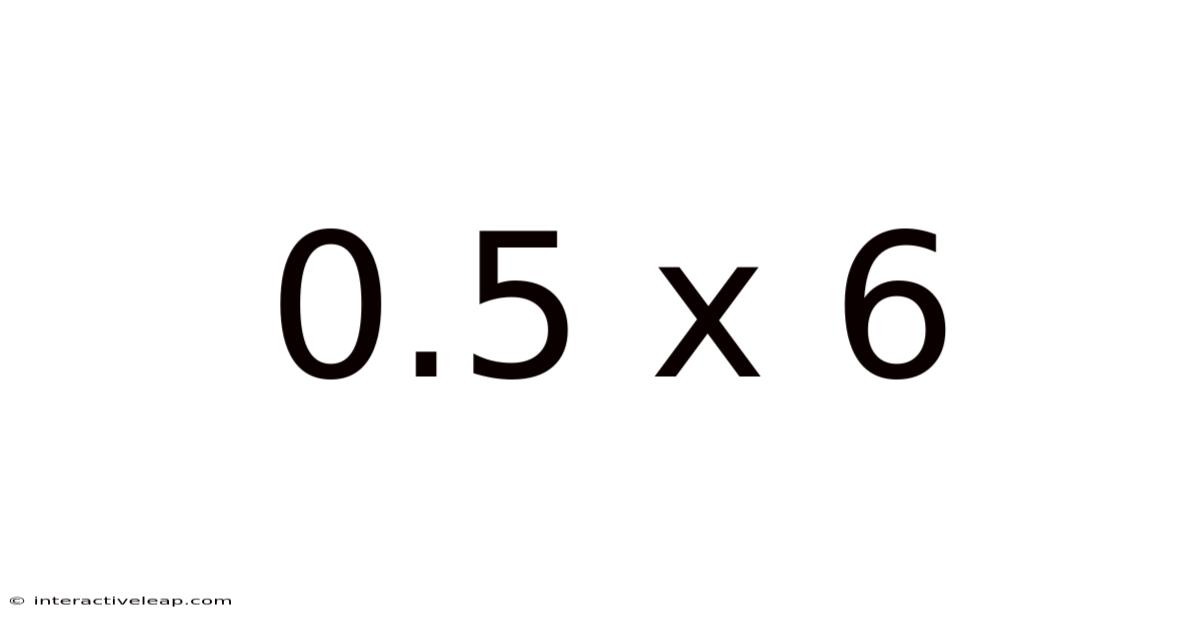
Table of Contents
Unveiling the Mysteries of 0.5 x 6: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 0.5 x 6, delving far beyond the immediate answer. We'll uncover the underlying mathematical principles, explore practical applications across various fields, and address common misconceptions surrounding decimal multiplication. This journey will equip you with a deeper understanding not just of this specific equation, but of the broader concepts it represents. The exploration will include visual representations, real-world examples, and frequently asked questions to ensure a comprehensive learning experience.
Understanding the Fundamentals: Decimals and Multiplication
Before diving into 0.5 x 6, let's establish a firm understanding of the components involved. 0.5, or one-half, is a decimal representation of a fraction. Decimals are a way of expressing numbers that are not whole numbers. They use a base-ten system, with each digit to the right of the decimal point representing a decreasing power of ten (tenths, hundredths, thousandths, and so on). 6 is a whole number, a positive integer.
Multiplication itself is a fundamental arithmetic operation that represents repeated addition. For example, 6 x 2 means adding 6 to itself two times (6 + 6 = 12). However, when dealing with decimals, the concept remains the same, though the process might appear slightly different.
Calculating 0.5 x 6: Multiple Approaches
There are several ways to calculate 0.5 x 6, each offering unique insights into the underlying mathematical principles:
1. Direct Decimal Multiplication:
The most straightforward method involves treating the decimal as a whole number during the multiplication process and then adjusting the decimal place in the final answer.
- Ignore the decimal point initially: 5 x 6 = 30
- Count the number of digits after the decimal point in the original decimal number (0.5 has one digit after the decimal).
- Place the decimal point in the result, so that there is one digit after the decimal point: 3.0 (or simply 3)
Therefore, 0.5 x 6 = 3
2. Fraction Conversion:
Converting the decimal to a fraction provides another approach. Remember that 0.5 is equivalent to 1/2. The calculation then becomes:
(1/2) x 6 = 6/2 = 3
This method highlights the relationship between fractions and decimals and reinforces the concept of multiplication as scaling or finding a portion of a whole.
3. Visual Representation:
Visual aids can greatly enhance understanding. Imagine a rectangle divided into two equal halves. If each half represents 0.5, and we take six of these halves, we effectively have three whole rectangles. This visual representation directly demonstrates that 0.5 x 6 = 3.
4. Repeated Addition:
As multiplication is repeated addition, we can visualize 0.5 x 6 as adding 0.5 six times:
0.5 + 0.5 + 0.5 + 0.5 + 0.5 + 0.5 = 3.0
This approach reinforces the fundamental definition of multiplication and is particularly helpful for beginners.
Real-World Applications of 0.5 x 6 and Similar Calculations
The seemingly simple calculation 0.5 x 6, and its related principles, have countless applications in various real-world scenarios:
-
Cooking and Baking: Recipes often require half of an ingredient. If a recipe calls for 6 cups of flour, and you only want to make half the recipe, you'd need 0.5 x 6 = 3 cups of flour.
-
Shopping: If an item costs $6 and you buy half of it (e.g., half a kilogram of fruit), the calculation 0.5 x 6 determines the cost.
-
Construction and Engineering: Calculations involving dimensions and material quantities often involve decimals. Determining the length of a beam that's half the length of a 6-meter beam would use this principle.
-
Finance: Calculating half of a discount, interest, or commission often requires decimal multiplication. For example, a 6% interest rate halved would be 3%.
-
Science: Many scientific formulas and calculations involve decimals and fractions, making a firm understanding of decimal multiplication crucial.
Expanding the Understanding: Beyond 0.5 x 6
Understanding 0.5 x 6 is a stepping stone to grasping more complex decimal multiplication. The principles discussed extend to calculations involving:
- Larger decimals: 0.75 x 6, 1.2 x 6, etc., all follow the same fundamental principles.
- More complex equations: The ability to calculate 0.5 x 6 seamlessly integrates into more complex calculations involving addition, subtraction, and division.
- Algebra: Understanding decimal multiplication is vital for solving algebraic equations involving decimals and variables.
Addressing Common Misconceptions
Several common misconceptions surround decimal multiplication:
-
Incorrect placement of the decimal point: This is the most frequent error. Students often misplace the decimal point in the final answer, leading to inaccurate results. Careful attention to the number of digits after the decimal point is crucial.
-
Treating decimals as separate entities: Some students try to multiply the whole number and the decimal part separately, which is incorrect. The decimal should be treated as part of a single number during the multiplication process.
-
Confusion with addition/subtraction: Decimal multiplication is distinct from decimal addition and subtraction. The processes and results are different.
Frequently Asked Questions (FAQ)
Q1: What happens if the decimal number has more than one digit after the decimal point?
A1: The process remains the same. You multiply as if the decimal point were not there, and then place the decimal point in the result such that the number of digits after the decimal point equals the total number of digits after the decimal point in the original numbers. For example, 0.25 x 6: 25 x 6 = 150. Since there are two digits after the decimal in 0.25, the answer is 1.50 (or 1.5).
Q2: Can I use a calculator for this type of calculation?
A2: Yes, calculators are helpful tools for verifying your work or performing more complex calculations. However, understanding the underlying principles is crucial for problem-solving and developing mathematical fluency.
Q3: Why is it important to learn decimal multiplication?
A3: Decimal multiplication is a fundamental skill applied across numerous disciplines and real-life scenarios. Mastering this skill enhances your overall mathematical proficiency and problem-solving abilities.
Conclusion: Mastering the Basics for Future Success
The seemingly simple calculation 0.5 x 6 unlocks a world of understanding in decimal multiplication and its broader applications. By mastering this foundational concept, you build a strong base for tackling more complex mathematical problems. The various approaches outlined in this article—direct multiplication, fraction conversion, visual representation, and repeated addition—offer diverse pathways to understanding this fundamental concept. Remember, practice is key to solidifying your knowledge and building confidence in your mathematical abilities. Continue exploring different decimal multiplication problems, and you'll soon find yourself adept at handling these calculations with ease and accuracy. The ability to confidently perform calculations like 0.5 x 6 is not just about getting the right answer; it's about developing a deeper, more intuitive understanding of numbers and their relationships.
Latest Posts
Latest Posts
-
2 X 3x
Sep 22, 2025
-
28divided By 3
Sep 22, 2025
-
Itp Vs Ttp
Sep 22, 2025
-
10 X 365
Sep 22, 2025
-
40 Divide 3
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 0.5 X 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.