0.3 Of 13750
interactiveleap
Sep 23, 2025 · 5 min read
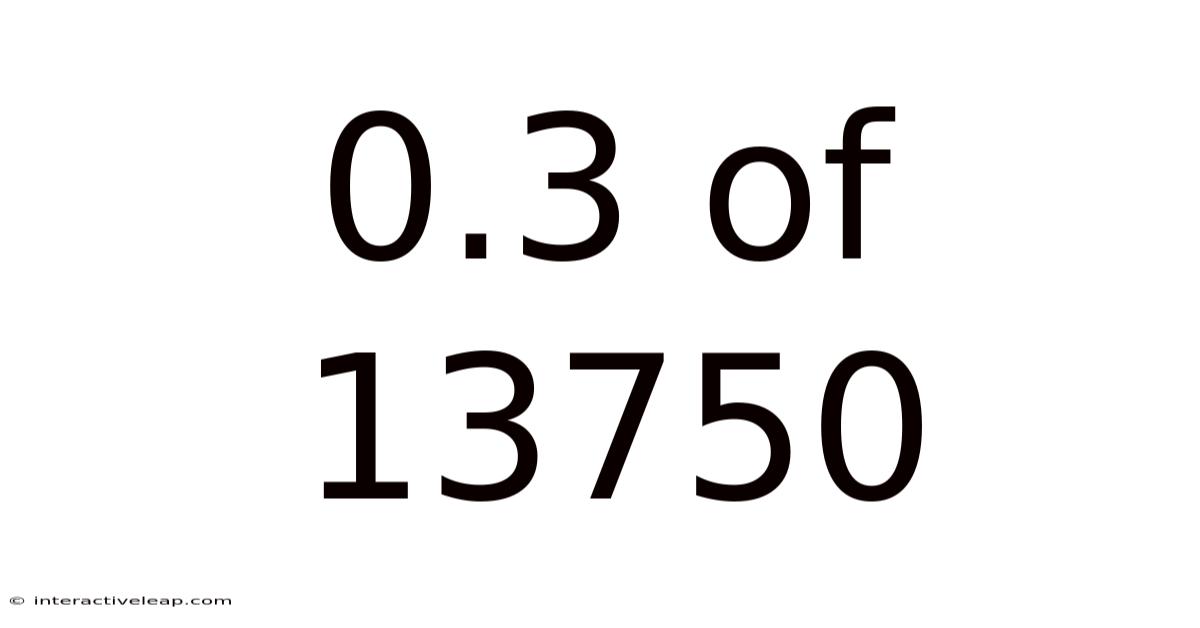
Table of Contents
Unveiling the Mystery: Calculating 0.3 of 13750 and Understanding Percentages
This article delves into the seemingly simple yet fundamentally important concept of calculating percentages. Specifically, we'll explore how to determine 0.3 (or 30%) of 13750, breaking down the process step-by-step and exploring the broader applications of percentage calculations in various fields. This guide is designed for all levels, from those needing a quick refresher to those seeking a deeper understanding of the underlying mathematical principles. Understanding percentages is crucial in numerous aspects of life, from financial planning and budgeting to analyzing data and interpreting statistical information. Let's begin!
Understanding Percentages: A Foundational Concept
Before diving into the calculation of 0.3 of 13750, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. This fundamental understanding is key to tackling percentage calculations efficiently.
Methods for Calculating 0.3 of 13750
There are several ways to calculate 0.3 of 13750. We'll explore two common methods: using multiplication and using fractions.
Method 1: Using Multiplication
This is perhaps the most straightforward method. We simply multiply the number (13750) by the percentage expressed as a decimal (0.3):
13750 x 0.3 = 4125
Therefore, 0.3 of 13750 is 4125.
Method 2: Using Fractions
We can also express 0.3 as a fraction. 0.3 is equivalent to 3/10. Therefore, we can calculate 0.3 of 13750 as follows:
(3/10) x 13750 = (3 x 13750) / 10 = 41250 / 10 = 4125
Again, we arrive at the same answer: 4125.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world situations. Here are some examples:
-
Finance: Calculating interest on loans, determining discounts, understanding tax rates, and analyzing investment returns all rely heavily on percentage calculations. For example, understanding a 5% interest rate on a loan or a 20% discount on a purchase requires a clear grasp of percentages.
-
Business: Analyzing sales figures, calculating profit margins, determining market share, and projecting future growth all involve extensive use of percentage calculations. For instance, a business might want to determine what percentage of its total sales come from a specific product line.
-
Science: Percentages are frequently used in scientific studies and data analysis. For instance, researchers might calculate the percentage of participants in a study who responded positively to a particular treatment.
-
Everyday Life: Calculating tips at restaurants, understanding sales tax, and determining the percentage of ingredients in a recipe all involve the application of percentage calculations. For example, calculating a 15% tip on a restaurant bill is a common real-world application of percentages.
-
Statistics: Percentages are fundamental in presenting and interpreting statistical data. For example, election results are often reported as percentages of the total votes cast.
Beyond the Basics: Working with Different Percentage Forms
While we’ve focused on 0.3 (or 30%), let's explore how to handle percentages presented in different formats.
-
Percentages greater than 100%: A percentage greater than 100% indicates a value exceeding the original amount. For example, if something increases by 150%, it means it has become 250% of its original value (100% + 150% = 250%).
-
Percentages less than 1%: These percentages can be calculated by converting them to decimals (e.g., 0.5% = 0.005) and then multiplying as usual.
-
Percentages expressed as fractions: As demonstrated earlier, converting fractions to decimals simplifies the calculation.
Troubleshooting Common Percentage Calculation Mistakes
Several common errors can arise when working with percentages. Here are a few to watch out for:
-
Incorrect decimal conversion: Ensure you accurately convert percentages to decimals before multiplying. For instance, 5% should be converted to 0.05, not 0.5.
-
Misinterpreting percentage increases/decreases: Remember that a percentage increase or decrease is relative to the original value.
-
Order of operations: Follow the correct order of operations (PEMDAS/BODMAS) when performing calculations involving multiple operations.
Advanced Applications: Compound Interest and Percentage Change
Let's briefly explore two advanced applications:
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. The formula is A = P (1 + r/n)^(nt), where A is the final amount, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years.
-
Percentage Change: This measures the change between two values as a percentage of the original value. The formula is [(New Value - Old Value) / Old Value] x 100%.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to calculate percentages?
A1: The easiest method is generally using multiplication. Convert the percentage to a decimal and multiply it by the number.
Q2: How do I calculate a percentage increase?
A2: Use the formula: [(New Value - Old Value) / Old Value] x 100%.
Q3: How do I calculate a percentage decrease?
A3: Use the same formula as a percentage increase; the result will be a negative number indicating a decrease.
Q4: What if I need to calculate a percentage of a percentage?
A4: Convert both percentages to decimals and multiply them together. For example, 10% of 20% is 0.1 x 0.2 = 0.02 or 2%.
Q5: Are there any online tools to help with percentage calculations?
A5: Yes, many online calculators are available to assist with percentage calculations. However, understanding the underlying principles is crucial for problem-solving in various contexts.
Conclusion: Mastering Percentage Calculations
Calculating 0.3 of 13750, as we've demonstrated, is a fundamental yet versatile skill. By understanding the core concepts and various calculation methods, you equip yourself with a powerful tool applicable across diverse fields. Remember to practice regularly, and don't hesitate to explore additional resources and examples to solidify your understanding. The ability to confidently handle percentage calculations opens doors to a more comprehensive grasp of numerical information and strengthens problem-solving abilities in various aspects of life, from personal finance to professional endeavors. Mastering percentages empowers you to make informed decisions and navigate the quantitative world with increased confidence and accuracy.
Latest Posts
Latest Posts
-
2 5 X 10
Sep 23, 2025
-
1700kg Into Tonnes
Sep 23, 2025
-
You Wish Meaning
Sep 23, 2025
-
Bubble Tiny Mighties
Sep 23, 2025
-
Korean Eye Makeup
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 0.3 Of 13750 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.