0.03 In Percentage
interactiveleap
Sep 16, 2025 · 5 min read
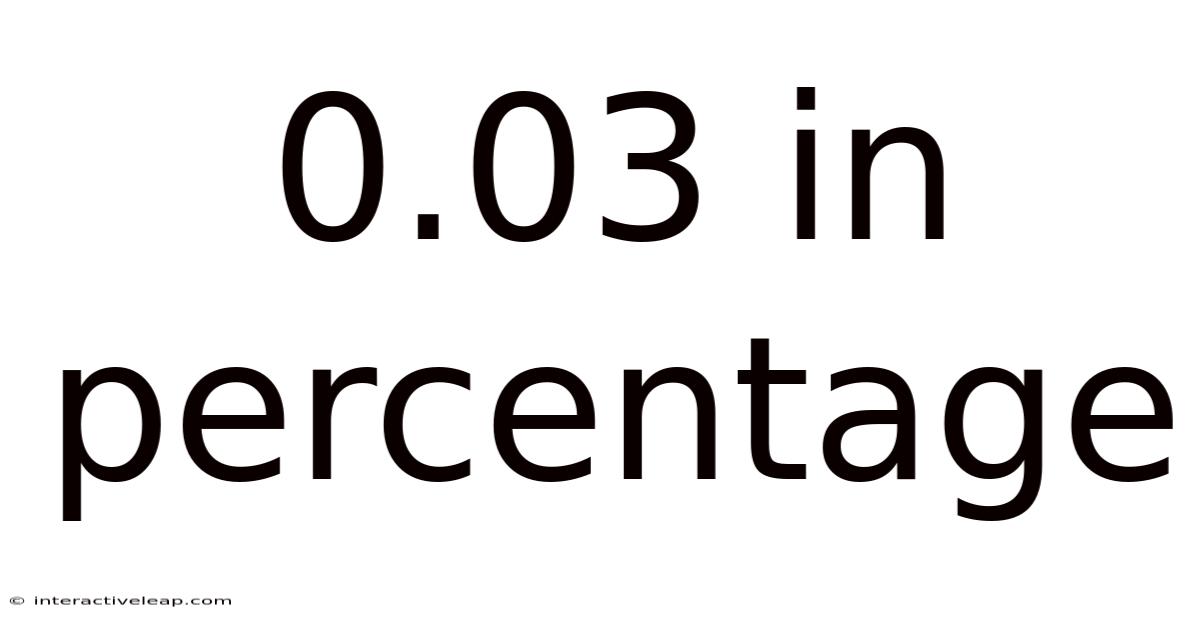
Table of Contents
Decoding 0.03: Understanding and Applying Percentages in the Real World
Many of us encounter percentages daily, whether calculating discounts at the mall, understanding interest rates on loans, or analyzing statistical data. But sometimes, even seemingly simple percentages can be tricky. This article delves deep into understanding the meaning and application of 0.03 as a percentage, breaking down its conversion, practical examples, and addressing common misconceptions. We'll explore how this seemingly small figure can have significant implications across various fields. Understanding 0.03% will not only boost your numerical literacy but also equip you with valuable skills for navigating everyday situations and more complex financial or statistical analyses.
From Decimal to Percentage: The Conversion Process
The core concept revolves around converting decimals to percentages. A percentage is simply a fraction out of 100. To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol. Let's break down 0.03:
- 0.03 x 100 = 3
Therefore, 0.03 is equivalent to 3%. This seemingly simple conversion is fundamental to understanding the significance of this value in various contexts.
Understanding the Significance of 3%
While 3% might seem small, its impact depends heavily on the context. A 3% increase in something large, like a national budget, represents a substantial amount. Conversely, a 3% increase in something small, like your daily allowance, might be negligible.
Let's illustrate with a few examples:
- Finance: A 3% interest rate on a savings account might seem modest, but over time, compound interest can significantly increase your savings. Conversely, a 3% increase in inflation erodes your purchasing power.
- Sales and Marketing: A 3% conversion rate in an online marketing campaign might indicate the effectiveness of your strategies. A 3% increase in sales could be significant depending on your baseline sales figures.
- Science and Statistics: In scientific research or statistical analysis, a 3% difference might be statistically significant, indicating a meaningful result depending on the experiment's nature and the sample size. A 3% margin of error in a survey indicates a level of uncertainty around the results.
Practical Applications of 0.03 (or 3%)
Let's explore practical scenarios where you might encounter 3%:
1. Calculating Discounts: Imagine a store offering a 3% discount on a $100 item. To calculate the discount, multiply the original price by 0.03 (or 3/100):
- $100 x 0.03 = $3
The discount is $3, making the final price $97.
2. Determining Interest Earned: If you have $5000 in a savings account with a 3% annual interest rate, the interest earned in one year would be:
- $5000 x 0.03 = $150
You would earn $150 in interest.
3. Calculating Tax: If the sales tax in your area is 3%, and you buy something for $200, the tax amount is:
- $200 x 0.03 = $6
The total cost including tax is $206.
4. Analyzing Growth Rates: Suppose a company's revenue increased by 3% this year. If the revenue last year was $1 million, the increase would be:
- $1,000,000 x 0.03 = $30,000
The revenue this year would be $1,030,000.
Beyond Simple Calculations: Understanding Compound Interest
The power of 3%, or 0.03, becomes more evident when considering compound interest. Compound interest means earning interest not only on your principal but also on accumulated interest. Over time, this effect significantly increases your returns.
For example, let's say you invest $1000 at a 3% annual interest rate compounded annually. After one year, you’ll have $1030. In the second year, you earn interest on $1030, not just the original $1000. This compounding effect becomes increasingly significant over longer periods. While the initial interest earned might seem small, the cumulative effect over many years is substantial.
Common Misconceptions about Percentages
Several common misunderstandings surrounding percentages can lead to miscalculations or misinterpretations. Let's address some key misconceptions:
- Adding Percentages Directly: You can't simply add percentages together if they refer to different bases. For example, a 10% increase followed by a 10% decrease does not result in a net change of 0%. The second 10% decrease is calculated on a new, larger base.
- Confusing Percentage Change with Percentage Points: A change from 5% to 8% is a 3 percentage point increase, but a 60% increase in the percentage itself. This distinction is crucial in many financial and statistical contexts.
- Ignoring the Base Value: The significance of a percentage change depends heavily on the base value. A 3% increase on a small number is far less impactful than a 3% increase on a large number.
Frequently Asked Questions (FAQ)
Q: How do I convert a percentage back to a decimal?
A: To convert a percentage to a decimal, divide the percentage by 100. For example, 3% becomes 3/100 = 0.03.
Q: What are some real-world examples of using 0.03% (not 3%)?
A: 0.03% is much smaller and might represent things like extremely low error rates in manufacturing, very small changes in scientific measurements, or minuscule changes in financial markets. It often appears in highly precise calculations or situations requiring a high degree of accuracy.
Q: How can I practice calculating percentages more effectively?
A: Practice regularly using real-life scenarios, like calculating discounts, interest, or tax. Use online calculators and practice problems to solidify your understanding.
Conclusion: The Power of Understanding 0.03%
Understanding 0.03, its conversion to 3%, and its applications is more than just a mathematical exercise. It's about developing a deeper understanding of percentages and their significant role in numerous aspects of our lives. From personal finance to scientific analysis and business decisions, the ability to accurately interpret and use percentages is a valuable skill. By mastering these fundamental concepts, you enhance your numerical literacy and improve your ability to make informed decisions in various aspects of your life. Remember, even a seemingly small number like 0.03 can have a profound impact depending on the context. Through careful consideration and precise calculation, you can harness the power of percentages to your advantage.
Latest Posts
Latest Posts
-
20 Of 200
Sep 16, 2025
-
Wishes Were Horses
Sep 16, 2025
-
21 Of 230
Sep 16, 2025
-
87 9kg In Stone
Sep 16, 2025
-
4000 60
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 0.03 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.