Y 3 X
interactiveleap
Sep 19, 2025 · 7 min read
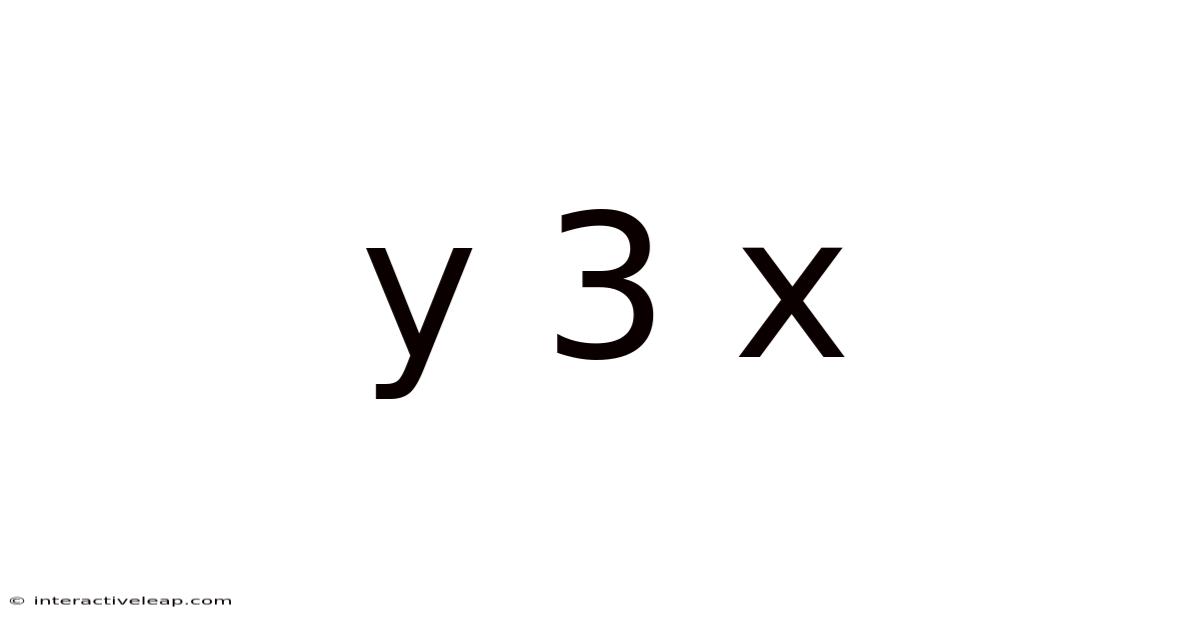
Table of Contents
Understanding Y = 3x: A Comprehensive Guide to Linear Equations
This article delves into the seemingly simple yet profoundly important linear equation, Y = 3x. We'll explore its meaning, applications, graphing techniques, and variations, providing a comprehensive understanding suitable for students and anyone curious about the fundamentals of algebra. This equation serves as a foundational building block for understanding more complex mathematical concepts and real-world applications.
Introduction: Decoding the Equation Y = 3x
At its core, Y = 3x represents a linear relationship between two variables, x and y. This means that for every change in x, there's a proportional change in y. The '3' in the equation is the slope or gradient, indicating the rate of change of y with respect to x. In simpler terms, for every 1-unit increase in x, y increases by 3 units. This constant rate of change is a defining characteristic of linear equations.
This equation is fundamental because it introduces key concepts like:
- Variables: x and y are variables that can take on different numerical values. x is often considered the independent variable (input), and y is the dependent variable (output).
- Slope: The coefficient '3' represents the slope, determining the steepness of the line when graphed. A positive slope indicates a positive correlation – as x increases, y increases.
- Intercept: This equation has a y-intercept of 0, meaning the line passes through the origin (0,0) on the Cartesian coordinate system.
Graphing Y = 3x: A Visual Representation
Visualizing the equation is crucial for understanding its behavior. To graph Y = 3x, follow these steps:
- Create a table of values: Choose several values for x and calculate the corresponding values for y using the equation. For example:
| x | y = 3x |
|---|---|
| -2 | -6 |
| -1 | -3 |
| 0 | 0 |
| 1 | 3 |
| 2 | 6 |
-
Plot the points: On a Cartesian coordinate plane, plot each (x, y) pair from the table.
-
Draw the line: Connect the plotted points with a straight line. This line represents all possible solutions to the equation Y = 3x. The line will pass through the origin (0,0) and have a positive slope, rising from left to right.
The graph clearly demonstrates the linear relationship: the points lie on a straight line, and the steepness of the line reflects the slope of 3.
Real-World Applications of Y = 3x
While seemingly abstract, Y = 3x and similar linear equations have countless real-world applications. Here are a few examples:
-
Direct Proportionality: If you earn $3 for every hour of work, your total earnings (y) are directly proportional to the number of hours worked (x). The equation Y = 3x perfectly models this scenario.
-
Conversion Factors: Converting units often involves linear relationships. For instance, if 1 meter equals 3 feet, the equation Y = 3x can convert meters (x) to feet (y).
-
Speed and Distance: If an object travels at a constant speed of 3 meters per second, the distance traveled (y) is directly proportional to the time (x). The equation Y = 3x describes this relationship.
-
Pricing: A simple pricing model might involve a constant cost per unit. If an item costs $3 each, the total cost (y) is Y = 3x, where x is the number of items.
Variations and Extensions of Y = 3x
The basic equation Y = 3x can be modified to represent more complex scenarios. Consider these variations:
-
Y = 3x + c: Adding a constant 'c' shifts the line vertically. 'c' represents the y-intercept, the point where the line intersects the y-axis. If c = 2, the equation becomes Y = 3x + 2, shifting the line 2 units upwards.
-
Y = mx: Replacing the '3' with a different constant 'm' changes the slope of the line. A larger 'm' means a steeper line, while a smaller 'm' means a less steep line. A negative 'm' results in a line sloping downwards from left to right, indicating a negative correlation.
-
More Complex Linear Equations: Equations like 2y = 6x + 4 can be simplified to the form Y = 3x + 2, demonstrating the fundamental relationship at its core.
Solving Equations Involving Y = 3x
Solving equations often involves finding the value of one variable given the value of the other.
-
Finding y given x: This is straightforward; simply substitute the given value of x into the equation and solve for y. For example, if x = 5, then y = 3 * 5 = 15.
-
Finding x given y: To find x given y, substitute the value of y into the equation and solve for x. For example, if y = 9, then 9 = 3x, which means x = 9/3 = 3.
These simple substitutions highlight the direct relationship between x and y in this linear equation.
The Significance of Slope in Y = 3x
The slope (3 in this case) is a crucial element of the equation. It quantifies the rate of change, indicating how much y changes for every unit change in x. A higher slope means a steeper line, representing a faster rate of change.
-
Positive Slope: A positive slope (like in Y = 3x) indicates a positive correlation – as x increases, y also increases.
-
Negative Slope: A negative slope (e.g., Y = -3x) indicates a negative correlation – as x increases, y decreases.
-
Zero Slope: A zero slope (e.g., Y = 0x + 2 or simply Y = 2) represents a horizontal line, meaning y remains constant regardless of the value of x.
-
Undefined Slope: An undefined slope occurs when the line is vertical (e.g., x = 2). In this case, x remains constant, and the equation isn't in the form Y = mx + c.
Understanding the Concept of Linearity
Y = 3x is a prime example of a linear equation because its graph is a straight line. Linearity implies a constant rate of change, meaning the relationship between the variables is consistent throughout. This contrasts with non-linear relationships, where the rate of change varies. Examples of non-linear relationships include exponential growth (y = a^x) or quadratic functions (y = ax^2 + bx + c).
Advanced Applications and Extensions
The principles illustrated by Y = 3x extend to far more complex mathematical models. Linear algebra, for instance, utilizes matrices and vectors to solve systems of linear equations, which are fundamental to numerous fields, including:
-
Computer Graphics: Transformations of objects in 3D space often involve linear equations.
-
Engineering: Structural analysis, circuit design, and many other engineering disciplines rely on systems of linear equations.
-
Economics: Linear programming is used to optimize resource allocation and solve economic problems.
-
Data Science: Linear regression, a statistical method used to model the relationship between variables, builds upon the principles of linear equations.
Frequently Asked Questions (FAQ)
Q: What happens if x is a negative number?
A: The equation works perfectly well with negative numbers. For example, if x = -2, then y = 3*(-2) = -6. The point (-2, -6) would still lie on the line.
Q: Can Y = 3x represent a real-world situation where x can only take on integer values?
A: Yes, absolutely. Consider the example of buying apples that cost $3 each. You can't buy half an apple, so x (number of apples) must be an integer. The equation still accurately describes the total cost.
Q: What if the equation is Y = 3x – 5? How does this change the graph?
A: The '-5' shifts the line down by 5 units along the y-axis. The slope remains 3, but the y-intercept is now -5.
Q: How is this equation different from Y = x?
A: Y = x has a slope of 1, meaning that for every 1-unit increase in x, y increases by only 1 unit. Y = 3x has a steeper slope, indicating a faster rate of change.
Conclusion: The Power of Simplicity
Y = 3x, while a simple equation, embodies fundamental principles of algebra and linear relationships. Understanding this equation provides a solid foundation for tackling more complex mathematical concepts and real-world problems. Its applications span diverse fields, highlighting the power of simple mathematical models in understanding and representing intricate phenomena. Mastering this foundational concept will undoubtedly enhance your mathematical skills and broaden your understanding of the world around you.
Latest Posts
Latest Posts
-
Graph Of Ph
Sep 19, 2025
-
58kgs In Stone
Sep 19, 2025
-
The Five Composers
Sep 19, 2025
-
40 Off 80
Sep 19, 2025
-
146lbs To Kg
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Y 3 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.