X3 X 3
interactiveleap
Sep 14, 2025 · 6 min read
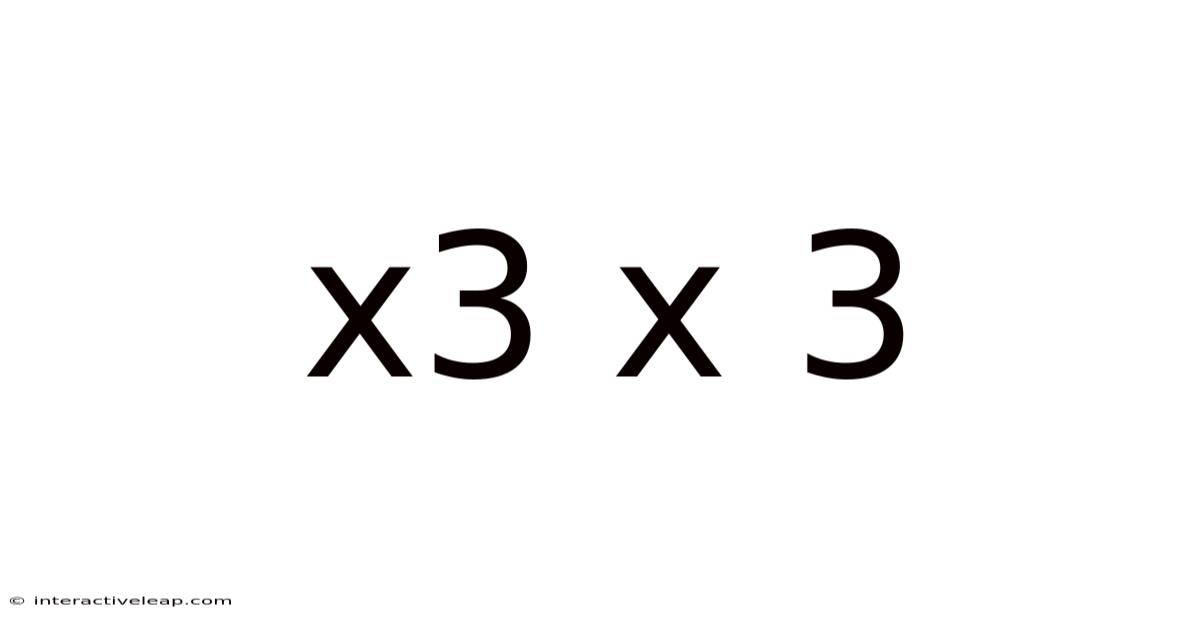
Table of Contents
Decoding X³ x 3: A Deep Dive into Cubic Functions and Their Applications
This article explores the mathematical expression X³ x 3, delving into its meaning, applications, and significance across various fields. We'll unravel the intricacies of cubic functions, their graphical representations, and how they model real-world phenomena. Understanding X³ x 3 provides a foundation for tackling more complex mathematical concepts and appreciating the power of mathematics in solving real-world problems. This exploration will be accessible to a wide range of readers, from high school students to those seeking a refresher on fundamental mathematical principles.
Understanding Cubic Functions: The Basics
At its core, X³ x 3 represents a cubic function, a type of polynomial function where the highest power of the variable (X) is 3. The general form of a cubic function is: f(x) = ax³ + bx² + cx + d, where 'a', 'b', 'c', and 'd' are constants, and 'a' is not equal to zero. In our specific case, X³ x 3 simplifies to f(x) = 3x³, meaning 'a' = 3, while 'b', 'c', and 'd' are all zero.
This simplified form allows us to focus on the fundamental characteristics of cubic functions without the complexities introduced by additional terms. The term '3x³' signifies that the output (f(x)) is three times the cube of the input (x). This means that as the input value increases, the output increases significantly faster than with a linear or quadratic function.
Graphical Representation: Visualizing the Cubic Function
The graph of a cubic function, like 3x³, is a curve with a distinct shape. Unlike linear equations which produce straight lines and quadratic equations which produce parabolas, cubic functions create curves with:
-
One inflection point: This is the point where the curve changes its concavity (from curving upwards to curving downwards, or vice-versa). For 3x³, the inflection point is at (0,0).
-
Potential local maxima and minima: While not present in the simplified 3x³ function, more complex cubic functions can possess one local maximum and one local minimum. These represent points where the function briefly stops increasing or decreasing before continuing in the opposite direction.
-
Unlimited range: The output of the function can range from negative infinity to positive infinity.
-
Symmetry about the origin: For the function 3x³, the graph exhibits origin symmetry, meaning it is symmetric about the point (0,0). This means that if you reflect the graph across both the x-axis and the y-axis, it will overlap perfectly with itself.
Understanding the graphical representation allows for a visual interpretation of the function's behavior and its relationship to the input values.
Steps to Graphing 3x³
Graphing a cubic function like 3x³ can be done using several methods:
- Creating a Table of Values: Choose several values for x (both positive and negative), calculate the corresponding values of f(x) = 3x³, and plot these points on a coordinate plane. Connecting these points will reveal the characteristic curve of the cubic function. For example:
| x | f(x) = 3x³ |
|---|---|
| -2 | -24 |
| -1 | -3 |
| 0 | 0 |
| 1 | 3 |
| 2 | 24 |
-
Using a Graphing Calculator or Software: Mathematical software or graphing calculators can quickly and accurately plot the function, providing a detailed visualization of the curve and its key features.
-
Identifying Key Features: By understanding the basic shape of a cubic function and its symmetry (in this case, origin symmetry), you can quickly sketch an approximate graph, even without detailed calculations.
Real-World Applications of Cubic Functions
The seemingly simple equation X³ x 3 and its broader class of cubic functions have surprising applications across a wide range of fields:
-
Engineering: Cubic functions are crucial in designing curves for roads, bridges, and architectural structures. The smooth transitions and optimal curvature achieved using cubic equations ensure structural integrity and aesthetic appeal.
-
Physics: Cubic functions can model various physical phenomena, such as the relationship between the volume and pressure of a gas (under certain conditions), or the trajectory of a projectile under specific circumstances.
-
Economics: Cubic functions can be used to model cost functions, production functions, and other economic relationships. The non-linear nature of cubic functions allows for a more realistic depiction of these often-complex interactions.
-
Computer Graphics: Cubic curves (specifically, Bezier curves and spline curves) are fundamental tools in creating smooth and natural-looking shapes in computer graphics, animation, and CAD software. These curves are mathematically defined using cubic polynomials, enabling precise control over the shape and curvature of lines and surfaces.
-
Medicine: In pharmacology, cubic functions can model drug concentration over time, helping researchers and clinicians understand how drugs are absorbed, metabolized, and eliminated from the body.
Beyond 3x³: Exploring More Complex Cubic Functions
While 3x³ provides a solid foundation for understanding cubic functions, many real-world applications involve more complex cubic equations. The general form, ax³ + bx² + cx + d, allows for a wider range of behaviors and modeling possibilities. The coefficients 'a', 'b', 'c', and 'd' influence the shape, position, and other characteristics of the graph:
-
'a': This coefficient determines the steepness of the curve. A larger value of 'a' results in a steeper curve, while a smaller value makes the curve gentler. A negative 'a' reflects the graph across the x-axis.
-
'b', 'c', and 'd': These coefficients shift and rotate the graph, influencing the location of the inflection point, the local maxima and minima, and the y-intercept.
Analyzing these coefficients allows for precise manipulation and fine-tuning of the cubic function to accurately model various phenomena.
Frequently Asked Questions (FAQ)
Q1: What is the derivative of 3x³?
A1: The derivative of 3x³ is 9x². This represents the instantaneous rate of change of the function at any given point.
Q2: How do I find the roots (x-intercepts) of a cubic function?
A2: Finding the roots of a cubic function can be more challenging than for linear or quadratic functions. While there are formulas for solving cubic equations, they are often complex. Numerical methods or graphing techniques are often used in practice. For 3x³, the only root is x = 0.
Q3: What is the difference between a cubic function and a cubic equation?
A3: A cubic function is a general mathematical expression of the form ax³ + bx² + cx + d. A cubic equation is a statement that sets a cubic function equal to a specific value (usually zero), such as ax³ + bx² + cx + d = 0. Solving a cubic equation means finding the values of x that satisfy the equation.
Q4: Can a cubic function have more than three roots?
A4: No, a cubic function can have at most three real roots (x-intercepts). It can also have complex roots, but these are not represented graphically on a standard x-y coordinate plane.
Conclusion: The Significance of X³ x 3 and Cubic Functions
The seemingly simple expression X³ x 3 unveils a rich world of mathematical concepts and applications. By understanding cubic functions, their graphical representations, and their real-world significance, we gain a deeper appreciation for the power and versatility of mathematics. From engineering marvels to intricate biological processes, cubic functions provide essential tools for modeling, analyzing, and understanding the complexities of our world. This exploration provides a foundation for further mathematical studies and highlights the enduring importance of this fundamental mathematical concept. Further exploration into calculus and numerical analysis will enhance your understanding and application of cubic functions even further.
Latest Posts
Latest Posts
-
49 4kg In Stone
Sep 14, 2025
-
107cm In Ft
Sep 14, 2025
-
70 Of 400
Sep 14, 2025
-
What Is Slumming
Sep 14, 2025
-
Jean Baptiste Greuze
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.