X 2 8.5
interactiveleap
Sep 19, 2025 · 7 min read
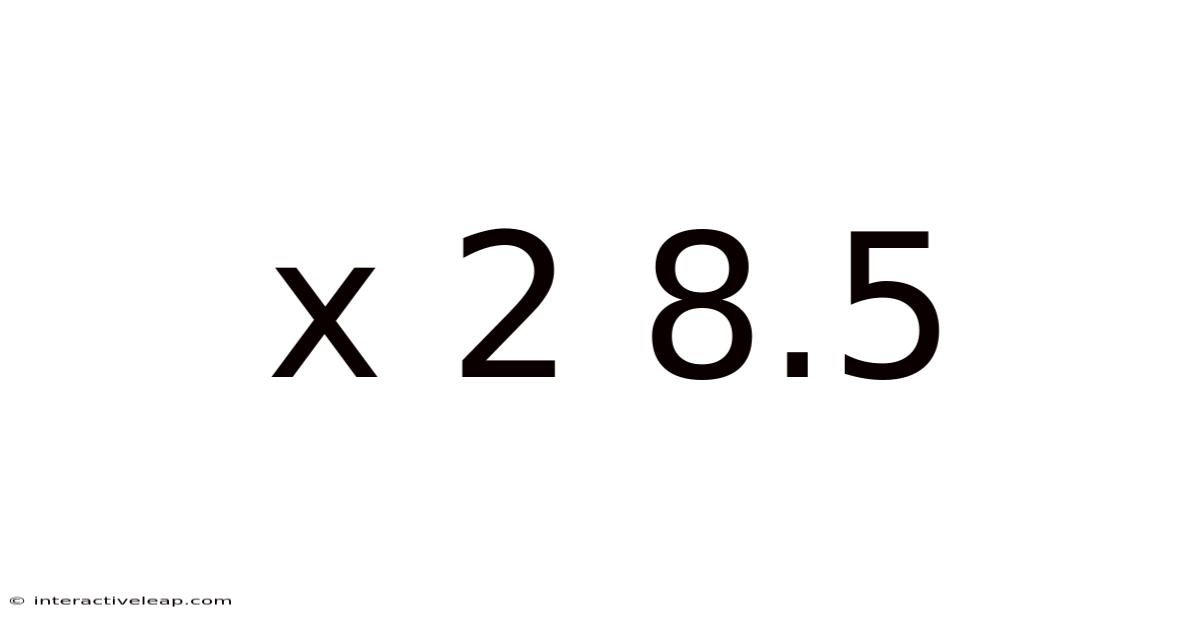
Table of Contents
Decoding X² + 8.5: A Deep Dive into Quadratic Expressions and Their Applications
This article explores the seemingly simple algebraic expression x² + 8.5, revealing its underlying complexities and wide-ranging applications in mathematics, science, and engineering. We'll dissect its components, examine its graphical representation, delve into solving related equations, and illustrate its practical use in real-world scenarios. Understanding this foundational concept unlocks doors to more advanced mathematical topics and problem-solving skills.
Introduction: Understanding the Basics
At first glance, x² + 8.5 might appear rudimentary. It's a quadratic expression, a type of polynomial where the highest power of the variable (x in this case) is 2. The expression comprises two terms: a quadratic term (x²) and a constant term (8.5). Understanding quadratic expressions is fundamental to algebra and forms the basis for solving a wide array of problems across various disciplines.
The expression itself doesn't represent a complete equation; it's an algebraic expression, meaning it doesn't equate to anything. To become an equation, it needs an equals sign and a value on the other side (e.g., x² + 8.5 = 0). This simple addition transforms it into a solvable problem with potential solutions for 'x'.
Graphical Representation: Visualizing the Parabola
A key to understanding x² + 8.5 lies in its graphical representation. When plotted on a Cartesian coordinate system (with x on the horizontal axis and y on the vertical axis), the equation y = x² + 8.5 produces a parabola.
-
Parabola Characteristics: This parabola opens upwards because the coefficient of the x² term (which is 1) is positive. It's a "U"-shaped curve, symmetrical about the y-axis. The vertex (lowest point) of the parabola is located at (0, 8.5). This means the parabola doesn't intersect the x-axis, indicating that the equation y = x² + 8.5 has no real roots (solutions where y=0).
-
Key Features to Observe: Analyzing the graph provides valuable insights into the behavior of the quadratic expression. The parabola's upward opening suggests that the value of the expression increases as the value of x moves further away from zero, both in the positive and negative directions. The y-intercept (where the parabola crosses the y-axis) is at 8.5, reflecting the constant term in the expression.
-
Transformations: We can understand the graphical behaviour better by comparing it to the simplest parabola, y=x². Adding 8.5 to the simplest form shifts the entire graph upwards by 8.5 units. This visual representation provides a clear link between the algebraic expression and its geometric interpretation.
Solving Quadratic Equations: Finding the Roots
While the expression x² + 8.5 doesn't directly lead to solving for x, related equations do. Consider the following equation:
x² + 8.5 = 0
This equation asks: "What value(s) of x, when squared and added to 8.5, result in zero?"
To solve this, we need to isolate x:
x² = -8.5
x = ±√(-8.5)
Here we encounter imaginary numbers. Since the square root of a negative number isn't a real number, this equation has no real solutions. The solutions are complex numbers, involving the imaginary unit 'i' (where i² = -1):
x = ±i√8.5 ≈ ±2.915i
This highlights a crucial aspect of quadratic equations: not all have real solutions. The nature of the solutions (real or complex) depends on the discriminant (b² - 4ac in the standard quadratic equation ax² + bx + c = 0). In this case, a=1, b=0, and c=8.5. The discriminant is 0² - 4(1)(8.5) = -34, a negative value indicating complex roots.
Applications in Various Fields
Although the specific equation x² + 8.5 = 0 doesn't directly model many real-world scenarios in its simplest form, the underlying principles of quadratic expressions and equations have countless applications:
-
Physics: Quadratic equations frequently appear in projectile motion calculations (e.g., determining the trajectory of a ball), describing the path of an object under the influence of gravity. The equation might need adjustments based on initial velocity and other factors.
-
Engineering: Quadratic equations play a role in structural design, electrical circuit analysis, and many other engineering disciplines. They often appear in models describing relationships between force, stress, strain and deflection in structures.
-
Economics: Quadratic functions can model supply and demand curves, helping economists analyze market equilibrium and price determination.
-
Computer Graphics: Parabolas and other quadratic curves are fundamental in computer graphics for creating smooth, curved shapes and paths.
-
Optimization Problems: Quadratic programming is a significant field of optimization, where the goal is to find the minimum or maximum value of a quadratic function subject to constraints. This is used extensively in finance, operations research, and machine learning.
Different Forms of Quadratic Equations and their Solutions
The equation x² + 8.5 = 0 is a simple form. However, quadratic equations frequently appear in more complex forms like ax² + bx + c = 0, where a, b, and c are constants. Various methods can solve these equations:
-
Factoring: This method involves expressing the quadratic expression as a product of two linear factors. It's most effective when the factors are easily identifiable.
-
Quadratic Formula: The quadratic formula provides a general solution for any quadratic equation:
x = [-b ± √(b² - 4ac)] / 2a
This formula is applicable even when factoring is difficult or impossible.
- Completing the Square: This technique involves manipulating the quadratic expression to create a perfect square trinomial, making it easier to solve for x.
The choice of method depends on the specific equation and the solver's preference. For equations like x² + 8.5 = 0, the quadratic formula is the most direct and efficient approach, clearly demonstrating the complex nature of the solutions.
Further Exploration: Beyond the Basics
The exploration of x² + 8.5 opens the door to many advanced mathematical concepts.
-
Calculus: The derivative of x² + 8.5 is 2x, representing the instantaneous rate of change of the function. This concept is fundamental in calculus for finding maximum and minimum points on curves, analyzing rates of change, and many other applications.
-
Linear Algebra: Quadratic forms are related to matrices and play a critical role in various areas of linear algebra and its applications, such as finding eigenvalues and eigenvectors.
-
Number Theory: The study of quadratic equations is also intertwined with number theory, which investigates the properties of integers and their relationships. Fermat's Last Theorem, for instance, deals with higher-degree polynomial equations, including quadratic ones as a foundational piece.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a quadratic expression and a quadratic equation?
A1: A quadratic expression is a mathematical phrase containing a variable raised to the second power (like x² + 8.5). A quadratic equation sets a quadratic expression equal to a value (like x² + 8.5 = 0). The equation requires solving for the variable.
Q2: Why are there no real solutions for x² + 8.5 = 0?
A2: Because squaring any real number always results in a non-negative number. Therefore, there's no real number that, when squared, results in a negative value (-8.5). The solutions involve imaginary numbers.
Q3: What are the practical applications of understanding quadratic equations?
A3: Quadratic equations are vital in many fields, including physics (projectile motion), engineering (structural analysis), economics (supply and demand), and computer graphics (curve generation). They are foundational tools for solving problems involving curves and optimizing quantities.
Q4: How do I choose the best method to solve a quadratic equation?
A4: Factoring is easiest if the equation factors simply. The quadratic formula always works, providing both real and complex solutions. Completing the square is useful for deriving other forms and understanding the equation’s properties.
Conclusion: The Significance of x² + 8.5
While seemingly simple, the expression x² + 8.5 serves as a gateway to a rich and extensive area of mathematics. Understanding its graphical representation, the process of solving related equations, and the underlying principles of quadratic expressions forms a solid foundation for tackling more complex mathematical challenges and unlocking their diverse applications across various scientific and engineering domains. The exploration of even this seemingly basic expression underscores the power and elegance of mathematics in describing and solving problems within our world. From the simple parabola to its complex implications, x² + 8.5 offers a fascinating journey into the heart of algebraic concepts and their real-world relevance.
Latest Posts
Latest Posts
-
15 Off 42
Sep 19, 2025
-
Best Plyometric Workouts
Sep 19, 2025
-
13cm To Mm
Sep 19, 2025
-
45 Of 20
Sep 19, 2025
-
144lb In Kg
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about X 2 8.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.