X 2 49
interactiveleap
Sep 18, 2025 · 5 min read
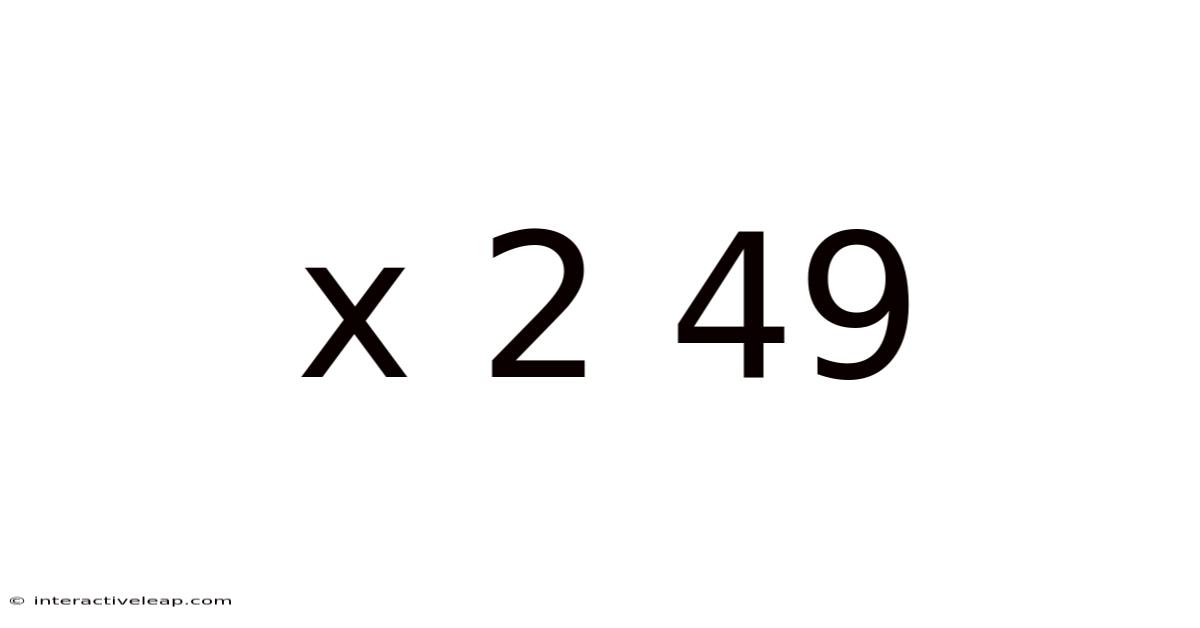
Table of Contents
Decoding x² + 49: A Deep Dive into Quadratic Expressions and Complex Numbers
Understanding quadratic expressions is fundamental to algebra and beyond. This article will delve into the seemingly simple expression x² + 49, exploring its properties, solutions, and the crucial role of complex numbers in its complete understanding. We'll move beyond simple factorization and uncover the rich mathematical landscape hidden within this seemingly straightforward equation. This exploration will be suitable for students and anyone interested in strengthening their grasp of algebra and complex number theory.
Introduction: The Puzzle of x² + 49
At first glance, x² + 49 appears simple. We're used to factoring quadratic expressions like x² - 49 (difference of squares), which easily factors to (x - 7)(x + 7). However, x² + 49 presents a different challenge. It's a sum of squares, and it doesn't factor neatly using real numbers. This seemingly simple equation opens the door to a deeper understanding of the number system and the power of complex numbers.
Why Real Numbers Fail
The quadratic formula, a cornerstone of algebra, provides solutions for equations of the form ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
In our case, x² + 49 = 0, meaning a = 1, b = 0, and c = 49. Substituting these values into the quadratic formula:
x = [0 ± √(0² - 4 * 1 * 49)] / 2 * 1
x = ± √(-196) / 2
The problem lies within the square root of a negative number. Real numbers don't allow us to take the square root of a negative value. This is where complex numbers come to the rescue.
Enter the Complex Numbers: Imaginary and Beyond
Complex numbers extend the real number system by introducing the imaginary unit, denoted as 'i', where i² = -1. This seemingly simple addition dramatically expands the possibilities of algebra and allows us to solve equations like x² + 49 = 0.
Using the imaginary unit, we can rewrite our solution:
x = ± √(-196) / 2 = ± √(196 * -1) / 2 = ± √(196)√(-1) / 2 = ± 14i / 2 = ±7i
Therefore, the solutions to x² + 49 = 0 are x = 7i and x = -7i. These are complex numbers, each consisting of a real part (0 in this case) and an imaginary part (±7).
Visualizing Complex Numbers: The Complex Plane
While real numbers can be represented on a single number line, complex numbers require a two-dimensional representation – the complex plane. The horizontal axis represents the real part, and the vertical axis represents the imaginary part. Our solutions, 7i and -7i, would be plotted on the imaginary axis, 7 units above and below the origin, respectively.
This visual representation helps us understand the nature of complex numbers and their relationship to real numbers. The complex plane provides a geometric interpretation that enhances our algebraic understanding.
Factoring with Complex Numbers
While we can't factor x² + 49 using only real numbers, we can factor it using complex numbers:
x² + 49 = (x - 7i)(x + 7i)
This factorization is a direct consequence of the solutions we found using the quadratic formula. The factors (x - 7i) and (x + 7i) represent the two complex roots.
The Significance of Complex Conjugates
Notice that the two complex roots, 7i and -7i, are complex conjugates. Complex conjugates are pairs of complex numbers that have the same real part but opposite imaginary parts. This relationship is important in many areas of mathematics, including solving polynomial equations and working with complex functions. The product of complex conjugates always results in a real number. In our case:
(x - 7i)(x + 7i) = x² - (7i)² = x² - 49i² = x² + 49 (since i² = -1)
Applications of Complex Numbers: Beyond the Classroom
While complex numbers might seem abstract, they have profound real-world applications. They are fundamental to:
- Electrical Engineering: Analyzing alternating current circuits and signal processing. The imaginary unit is crucial for representing impedance and phase shifts.
- Quantum Mechanics: Describing the wave function of particles and understanding quantum phenomena.
- Fluid Dynamics: Modeling complex fluid flows and analyzing wave propagation.
- Signal Processing: Analyzing and manipulating signals in various fields like telecommunications and image processing.
Solving Related Quadratic Equations
Understanding the solution to x² + 49 = 0 provides a foundation for tackling related quadratic equations. For example, consider:
- x² + k² = 0: This equation has solutions x = ±ki, where k is a real number.
- ax² + k² = 0: This equation has solutions x = ±ki/√a, for a>0.
- x² + 49 = c: This equation has solutions x = ±√(c-49) if c ≥ 49, or ±i√(49-c) if c < 49.
These examples demonstrate the wide applicability of the concepts we've explored. The techniques used to solve x² + 49 = 0 are readily adaptable to a broader range of quadratic equations.
Frequently Asked Questions (FAQ)
Q1: Why is it important to understand complex numbers?
A1: Complex numbers extend the real number system, allowing us to solve equations that are unsolvable using only real numbers. They have widespread applications in various fields, including engineering, physics, and computer science.
Q2: Can all quadratic equations be solved using the quadratic formula?
A2: Yes, the quadratic formula provides solutions for all quadratic equations, including those with real or complex roots.
Q3: What is the difference between real and imaginary numbers?
A3: Real numbers are numbers that can be plotted on a number line. Imaginary numbers are multiples of the imaginary unit 'i', where i² = -1. Complex numbers combine both real and imaginary parts.
Q4: How do I visualize complex numbers?
A4: Complex numbers are visualized on the complex plane, where the horizontal axis represents the real part and the vertical axis represents the imaginary part.
Q5: Are there other ways to solve x² + 49 = 0 besides the quadratic formula?
A5: While the quadratic formula is a direct and powerful method, you could also approach this by considering x² = -49 and then introducing the concept of 'i' directly to find the solutions.
Conclusion: A Deeper Understanding
This exploration of x² + 49 has demonstrated that even seemingly simple algebraic expressions can lead to deeper mathematical concepts. The inability to factor x² + 49 using real numbers highlighted the limitations of the real number system and paved the way for understanding the elegance and power of complex numbers. The journey through this seemingly simple equation provides a solid foundation for further exploration into the world of quadratic expressions, complex analysis, and their far-reaching applications. Remember, mathematics is not just about finding answers; it's about understanding the underlying principles and expanding our mathematical horizons.
Latest Posts
Latest Posts
-
5mg To Milliliters
Sep 18, 2025
-
62cms In Inches
Sep 18, 2025
-
What Is Cnfm
Sep 18, 2025
-
Dreaming War Meaning
Sep 18, 2025
-
Sentence Using Aloud
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about X 2 49 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.