X 2 36
interactiveleap
Sep 20, 2025 · 6 min read
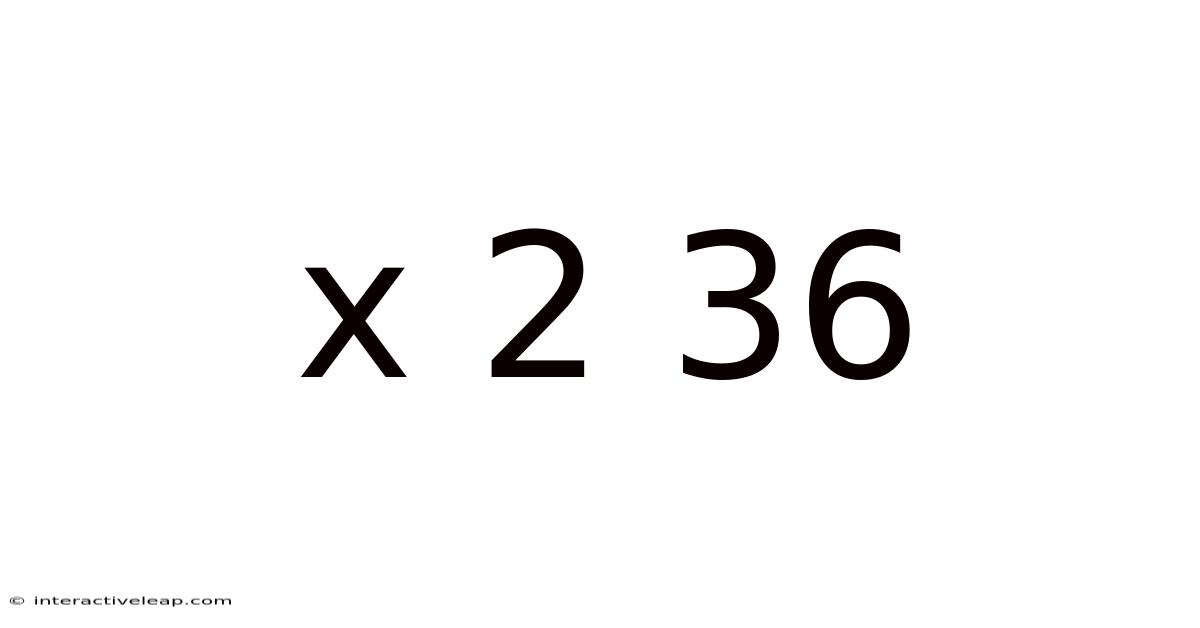
Table of Contents
Decoding x² + 36: A Deep Dive into Quadratic Expressions and Their Applications
This article explores the seemingly simple algebraic expression x² + 36, delving into its properties, potential solutions, its place within the broader context of quadratic equations, and its surprising applications across various fields. We'll move beyond simple factorization to understand the nuances of complex numbers and their significance in solving seemingly unsolvable equations. Understanding x² + 36 opens doors to a richer appreciation of algebra and its real-world impact.
Introduction: Beyond the Obvious
At first glance, x² + 36 appears straightforward. It's a quadratic expression – a polynomial of degree two – and a common sight in algebra classes. However, a closer examination reveals complexities that unveil fundamental concepts in mathematics, particularly concerning the nature of solutions and the power of complex numbers. Unlike expressions like x² - 36, which can be easily factored using the difference of squares, x² + 36 presents a unique challenge, leading us into the fascinating world of imaginary and complex numbers.
Understanding Quadratic Equations: The Foundation
Before dissecting x² + 36, let's establish a firm grasp on quadratic equations. A standard quadratic equation takes the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants and 'a' is not equal to zero. The solutions to this equation, often represented as 'x', represent the points where the parabolic graph of the equation intersects the x-axis. These solutions can be found using various methods, including factoring, completing the square, and the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
The term inside the square root, b² - 4ac, is known as the discriminant. It determines the nature of the solutions:
- b² - 4ac > 0: Two distinct real solutions.
- b² - 4ac = 0: One real solution (a repeated root).
- b² - 4ac < 0: Two complex solutions (involving imaginary numbers).
Solving x² + 36 = 0: Entering the Realm of Complex Numbers
Our expression, x² + 36, can be rewritten as a quadratic equation: x² + 0x + 36 = 0. Here, a = 1, b = 0, and c = 36. Let's apply the quadratic formula:
x = [-0 ± √(0² - 4 * 1 * 36)] / 2 * 1
x = ± √(-144) / 2
This introduces the crucial concept of the imaginary unit, denoted as 'i', where i² = -1. We can rewrite the equation as:
x = ± √(144 * -1) / 2
x = ± √(144) * √(-1) / 2
x = ± 12i / 2
x = ± 6i
Therefore, the solutions to x² + 36 = 0 are x = 6i and x = -6i. These are complex numbers, comprising a real part (0 in this case) and an imaginary part (±6).
Complex Numbers: A Deeper Exploration
Complex numbers are numbers of the form a + bi, where 'a' is the real part and 'b' is the imaginary part. They extend the number system beyond real numbers, allowing us to solve equations that have no real solutions. The set of complex numbers is denoted by ℂ. Complex numbers are crucial in various fields, including:
- Electrical Engineering: Representing alternating currents and voltages.
- Quantum Mechanics: Describing the wave function of particles.
- Signal Processing: Analyzing and manipulating signals.
- Fluid Dynamics: Modeling complex flow patterns.
The introduction of complex numbers signifies a significant expansion of mathematical tools and their applications in solving real-world problems. The seemingly simple equation x² + 36 = 0 provides a gateway into this important mathematical concept.
Graphical Representation and the Complex Plane
While real solutions to quadratic equations can be easily visualized on a number line, complex solutions require a two-dimensional representation – the complex plane. The complex plane, also known as the Argand diagram, uses the horizontal axis (real axis) to represent the real part and the vertical axis (imaginary axis) to represent the imaginary part of a complex number. Our solutions, 6i and -6i, would be represented as points on the imaginary axis, 6 units above and below the origin, respectively. This visualization helps understand the geometric interpretation of complex numbers and their operations.
Factorization Using Complex Numbers
While x² + 36 cannot be factored using real numbers, we can factor it using complex numbers:
x² + 36 = (x - 6i)(x + 6i)
This factorization is consistent with the solutions we obtained using the quadratic formula. It demonstrates that even expressions that seem unfactorable in the real number system can be factored within the broader context of complex numbers.
Applications in Advanced Mathematics
The concept explored through x² + 36 forms the basis for understanding more advanced mathematical concepts:
- Polynomial Equations: The solutions to higher-degree polynomial equations often involve complex numbers.
- Calculus: Complex numbers play a vital role in complex analysis, a branch of calculus dealing with functions of complex variables.
- Abstract Algebra: Complex numbers form a field, a fundamental structure in abstract algebra.
Frequently Asked Questions (FAQs)
-
Q: Why are complex numbers important?
- A: Complex numbers extend the number system, enabling solutions to equations that have no real solutions and providing essential tools for various scientific and engineering disciplines.
-
Q: Can I solve x² + 36 = 0 using other methods besides the quadratic formula?
- A: While the quadratic formula is a direct and efficient method, you could also try completing the square, though this will still lead you to the use of the imaginary unit 'i'.
-
Q: What is the significance of the discriminant in this case?
- A: The discriminant (b² - 4ac) is -144, which is negative, indicating that the quadratic equation has two complex conjugate solutions, as we found: 6i and -6i.
-
Q: Are complex numbers just theoretical, or do they have practical applications?
- A: Complex numbers are far from theoretical. They have widespread practical applications in electrical engineering, quantum mechanics, signal processing, and many other fields.
-
Q: Is it possible to visualize x² + 36 graphically in a way that shows the complex roots?
- A: Yes. The graph of y = x² + 36 is a parabola that opens upwards and never intersects the x-axis (the real number line). However, the complex roots can be visualized on the complex plane, as points located on the imaginary axis.
Conclusion: A Simple Expression, Profound Implications
The seemingly simple algebraic expression x² + 36, while appearing initially unfactorable, serves as a powerful introduction to the world of complex numbers and their significance. By exploring its solutions, we've delved into fundamental concepts of quadratic equations, the nature of solutions, and the crucial role of the imaginary unit 'i'. This understanding extends beyond basic algebra, providing a foundational base for more advanced mathematical concepts and their practical applications in various fields. The journey from a simple expression to the intricacies of complex numbers highlights the beauty and power of mathematics, demonstrating how seemingly unsolvable problems can be addressed with the right mathematical tools. It underscores the importance of continuous exploration and a deeper understanding of fundamental mathematical principles.
Latest Posts
Latest Posts
-
4 8kg To Lbs
Sep 20, 2025
-
The Perfume Book
Sep 20, 2025
-
Empirical Formula Examples
Sep 20, 2025
-
Nickname William Shakespeare
Sep 20, 2025
-
Eric Schlosser Author
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about X 2 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.