X 2 16
interactiveleap
Sep 23, 2025 · 6 min read
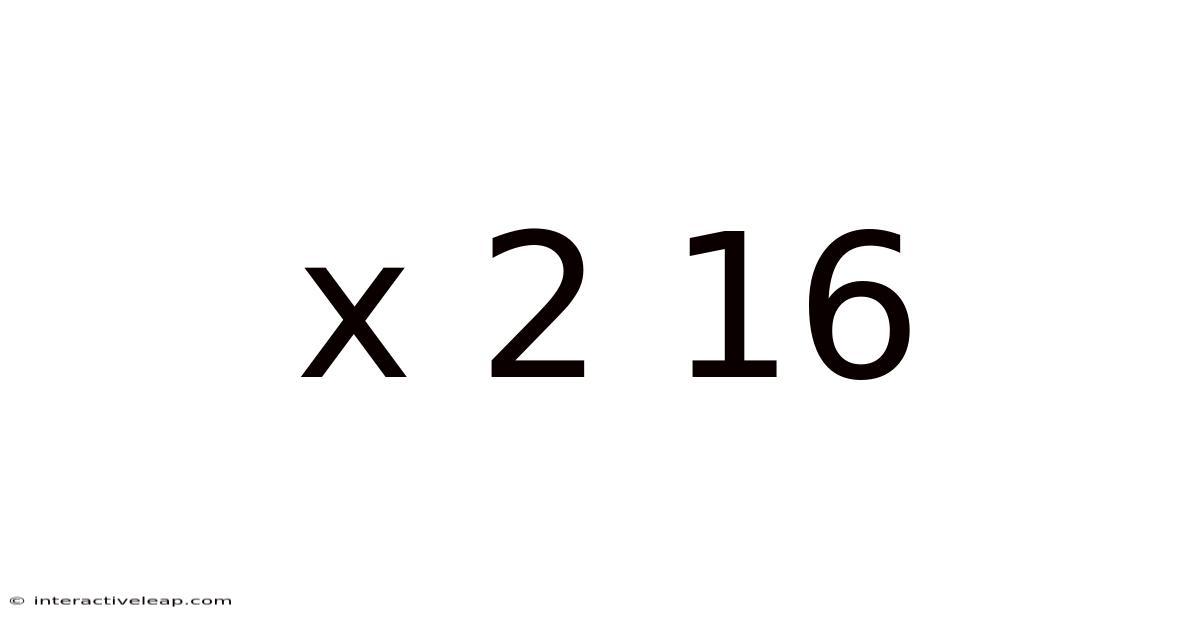
Table of Contents
Decoding x² + 16: A Deep Dive into Quadratic Equations and Complex Numbers
This article explores the seemingly simple expression x² + 16, delving into its solutions, the underlying mathematical concepts, and its significance within the broader context of algebra and number systems. We'll journey from basic quadratic equation solving to the fascinating world of complex numbers, ensuring a comprehensive understanding for readers of all levels. Understanding x² + 16 unlocks crucial concepts vital for advanced mathematics and related fields.
Introduction: Understanding Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, x) is 2. The general form is ax² + bx + c = 0, where a, b, and c are constants and a ≠ 0. Our specific equation, x² + 16 = 0, is a simplified form where b = 0 and c = 16. While seemingly simple, this equation introduces fundamental concepts in algebra and lays the groundwork for understanding more complex mathematical structures.
Solving x² + 16 = 0: The Real Number Limitation
Our first attempt at solving x² + 16 = 0 might involve subtracting 16 from both sides: x² = -16. At this point, we encounter a crucial limitation within the realm of real numbers. There is no real number that, when squared, results in a negative value. The square of any real number is always non-negative (zero or positive). This leads us to explore a broader number system capable of handling such equations: complex numbers.
Entering the Realm of Complex Numbers: Imaginary and Complex Units
To solve x² = -16, we introduce the imaginary unit, denoted as i. This unit is defined as the square root of -1: i² = -1. This seemingly simple definition opens up a whole new world of mathematical possibilities.
Now, we can rewrite our equation: x² = -16 = 16 * (-1) = 16i². Taking the square root of both sides, we get: x = ±√(16i²) = ±4i.
Therefore, the solutions to x² + 16 = 0 are x = 4i and x = -4i. These solutions are complex numbers. A complex number is a number that can be expressed in the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit. In our case, a = 0 and b = ±4.
Graphical Representation: Visualizing Complex Roots
While real number solutions can be easily plotted on a number line, complex numbers require a two-dimensional representation. This is typically done using a complex plane (also known as an Argand diagram). The horizontal axis represents the real part (a), and the vertical axis represents the imaginary part (b). The solutions 4i and -4i would be plotted on the imaginary axis, at +4 and -4 respectively. This visualization helps us grasp the geometric interpretation of complex roots.
The Fundamental Theorem of Algebra and its Implications
The Fundamental Theorem of Algebra states that a polynomial of degree n has exactly n roots (solutions), counting multiplicity, in the complex number system. Since x² + 16 is a polynomial of degree 2, it must have two roots. We've found these roots to be 4i and -4i, confirming the theorem. This theorem highlights the completeness of the complex number system in providing solutions for all polynomial equations.
Applications of Complex Numbers: Beyond the Abstract
While complex numbers might seem abstract, they have profound applications in various fields:
- Electrical Engineering: Complex numbers are crucial for analyzing alternating current (AC) circuits. Impedance, a measure of opposition to current flow, is often represented as a complex number.
- Quantum Mechanics: The mathematical framework of quantum mechanics heavily relies on complex numbers to describe wave functions and probabilities.
- Signal Processing: Complex numbers are used extensively in analyzing and manipulating signals, particularly in areas like digital signal processing (DSP).
- Fluid Dynamics: Complex analysis is used to solve certain types of fluid flow problems.
- Fractals and Chaos Theory: The Mandelbrot set, a famous fractal, is generated using iterative calculations involving complex numbers.
Expanding the Understanding: Factoring and the Difference of Squares
The equation x² + 16 = 0 can also be approached using factorization, though it requires extending our understanding beyond real numbers. We can rewrite the equation as:
x² - (4i)² = 0
This is now in the form of a difference of squares (a² - b² = (a + b)(a - b)), where a = x and b = 4i. Factoring, we get:
(x + 4i)(x - 4i) = 0
Setting each factor to zero gives us the same solutions: x = -4i and x = 4i. This approach reinforces the concept that complex numbers are necessary to fully factor certain quadratic expressions.
Further Exploration: Higher-Order Polynomials and Complex Roots
The principles discussed here extend to higher-order polynomial equations. For instance, a cubic equation (degree 3) will always have three complex roots (though some might be real numbers, which are a subset of complex numbers). The understanding of complex numbers is fundamental to solving and analyzing such equations.
Frequently Asked Questions (FAQ)
-
Q: Why are complex numbers necessary to solve x² + 16 = 0?
- A: Because the square of any real number is non-negative. To obtain a negative result (-16) when squaring, we need to introduce the imaginary unit i.
-
Q: Are complex numbers "imaginary" in the sense that they don't exist?
- A: The term "imaginary" is a historical artifact. Complex numbers are as valid and useful as real numbers, with significant applications in various fields of science and engineering. They simply expand the number system to include numbers with both real and imaginary components.
-
Q: Can I use a calculator to solve equations involving complex numbers?
- A: Many scientific calculators and mathematical software packages can handle complex number calculations. They typically use the notation a + bi or rectangular coordinates to represent complex numbers.
-
Q: What is the conjugate of a complex number?
- A: The conjugate of a complex number a + bi is a - bi. Conjugates are crucial in various operations involving complex numbers, such as division and finding magnitudes.
Conclusion: The Power and Elegance of Complex Numbers
The seemingly simple equation x² + 16 = 0 serves as a gateway to a deeper understanding of quadratic equations and the elegance of the complex number system. While initially challenging, the concept of the imaginary unit i expands the scope of algebra, enabling solutions to equations previously unsolvable within the real number system. The applications of complex numbers are vast, extending far beyond the realm of abstract mathematics and into various practical fields. Mastering this concept provides a solid foundation for tackling more advanced mathematical concepts and opens doors to a wider understanding of the world around us. The journey into the realm of complex numbers reveals the richness and power inherent within the seemingly simple.
Latest Posts
Latest Posts
-
Sodium Sulfide Formula
Sep 23, 2025
-
The Flower Carrier
Sep 23, 2025
-
85kilos In Stone
Sep 23, 2025
-
220mm Into Inches
Sep 23, 2025
-
U Wish Meaning
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about X 2 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.