Square Root 192
interactiveleap
Sep 21, 2025 · 5 min read
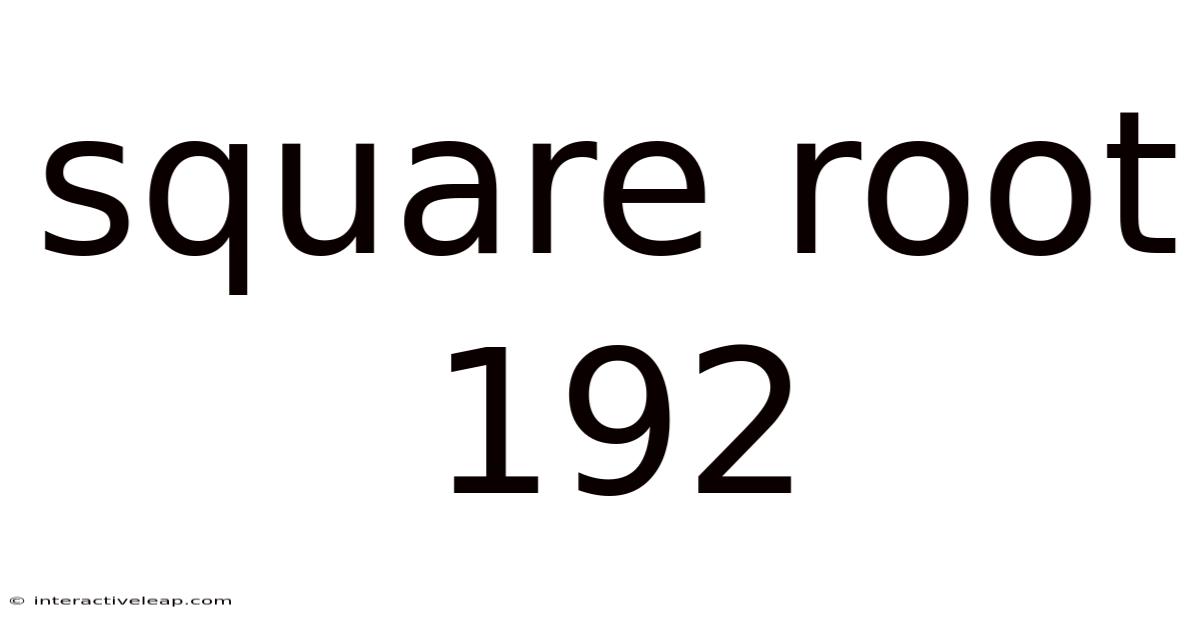
Table of Contents
Unveiling the Mysteries of √192: A Deep Dive into Square Roots and Simplification
Finding the square root of 192, denoted as √192, might seem like a simple arithmetic problem at first glance. However, understanding the process reveals a fascinating journey into the world of prime factorization, simplifying radicals, and appreciating the elegance of mathematics. This article will not only guide you through calculating √192 but also delve deeper into the underlying mathematical concepts, empowering you to tackle similar problems with confidence.
Introduction: Understanding Square Roots
Before we embark on our calculation, let's establish a foundational understanding of square roots. A square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. However, not all square roots result in whole numbers. Numbers like √192 produce irrational numbers, meaning their decimal representation goes on forever without repeating. This is where the concept of simplifying radicals becomes crucial. This process aims to express the square root in its simplest form, often involving a combination of a whole number and a simplified radical. Simplifying radicals enhances understanding and facilitates easier calculations in advanced mathematical contexts.
Step-by-Step Calculation of √192
The key to simplifying √192 lies in prime factorization. This involves breaking down the number into its prime factors – numbers divisible only by 1 and themselves. Let's break down 192 step-by-step:
-
Find the prime factorization of 192:
We can start by dividing 192 by the smallest prime number, 2:
192 ÷ 2 = 96 96 ÷ 2 = 48 48 ÷ 2 = 24 24 ÷ 2 = 12 12 ÷ 2 = 6 6 ÷ 2 = 3
Therefore, the prime factorization of 192 is 2 x 2 x 2 x 2 x 2 x 2 x 3, or 2⁶ x 3.
-
Rewrite the square root using the prime factorization:
Now we can rewrite √192 as √(2⁶ x 3).
-
Simplify the radical:
Remember that √(a x b) = √a x √b. We can use this property to simplify:
√(2⁶ x 3) = √(2⁶) x √3
Since √(2⁶) is equivalent to √(2² x 2² x 2²) = 2 x 2 x 2 = 8, our expression simplifies to:
8√3
Therefore, the simplified form of √192 is 8√3. This is the most accurate and simplified representation. Any decimal approximation will be an approximation, not the exact value.
Approximating the Decimal Value
While 8√3 is the exact and preferred form, it’s often helpful to have a decimal approximation. Using a calculator, we find that √3 ≈ 1.732. Therefore:
8√3 ≈ 8 x 1.732 ≈ 13.856
Keep in mind that this is an approximation. The value of √3 is irrational, meaning its decimal representation continues infinitely without repeating.
Understanding the Mathematical Concepts in Depth
Let's delve deeper into the mathematical principles that underpin our calculation:
-
Prime Factorization: This fundamental concept in number theory is crucial for simplifying radicals. Expressing a number as a product of its prime factors reveals its inherent structure and allows us to identify perfect squares, which simplifies the radical expression. The prime factorization is unique for every number, making it a powerful tool in various mathematical applications.
-
Radicals and Exponents: Square roots are essentially exponents raised to the power of 1/2. Understanding this connection bridges the gap between radicals and exponential notation. For example, √x = x¹/². This relationship is invaluable when dealing with more complex radical expressions involving higher roots.
-
Properties of Radicals: The ability to split radicals, as demonstrated in step 3 (√(a x b) = √a x √b), is a fundamental property that makes simplifying radicals possible. Understanding and applying this property correctly is essential for simplifying complex radical expressions.
Frequently Asked Questions (FAQ)
-
Why is simplifying radicals important? Simplifying radicals provides a more concise and manageable representation of the value. It improves readability and facilitates further calculations. In advanced mathematics, working with simplified radicals is often crucial for efficient problem-solving.
-
Can I use a calculator to find √192 directly? While a calculator will provide a decimal approximation, it won't give you the simplified radical form (8√3), which is often more valuable in mathematical contexts. The calculator provides a numerical answer, but the process of simplification provides a deeper understanding of the mathematical structure.
-
Are there other methods for simplifying square roots? Prime factorization is the most efficient and widely used method. However, you could also use trial and error to find perfect square factors within the number, but this becomes cumbersome for larger numbers. Prime factorization offers a systematic approach that works reliably for all numbers.
-
What if the number under the square root is negative? The square root of a negative number is an imaginary number, represented using the imaginary unit i, where i² = -1. The process of simplifying involves factoring out -1 and expressing the result in terms of i. This leads to the realm of complex numbers, which is a more advanced mathematical concept.
Conclusion: Mastering the Art of Square Root Simplification
Calculating and simplifying √192 is more than just finding a numerical answer; it's about understanding the underlying mathematical principles. Through prime factorization and the application of radical properties, we successfully simplified √192 to its most concise and accurate form: 8√3. This journey underscores the importance of foundational mathematical concepts and highlights the elegance and power of simplifying expressions to their simplest forms. Mastering these techniques not only enhances your arithmetic skills but also provides a strong foundation for tackling more advanced mathematical concepts in the future. Remember, the key is practice and a deep understanding of prime factorization and the properties of radicals. By understanding these concepts, you'll be well-equipped to tackle a wide range of square root problems with ease and confidence. So, continue practicing, explore further, and embrace the beauty of mathematics!
Latest Posts
Latest Posts
-
20 5 6
Sep 21, 2025
-
Sri Tirumalai Krishnamacharya
Sep 21, 2025
-
Emt Electrical Conduit
Sep 21, 2025
-
Loom With Beads
Sep 21, 2025
-
175cm To Inches
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Square Root 192 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.