Sqrt Of 180
interactiveleap
Sep 23, 2025 · 6 min read
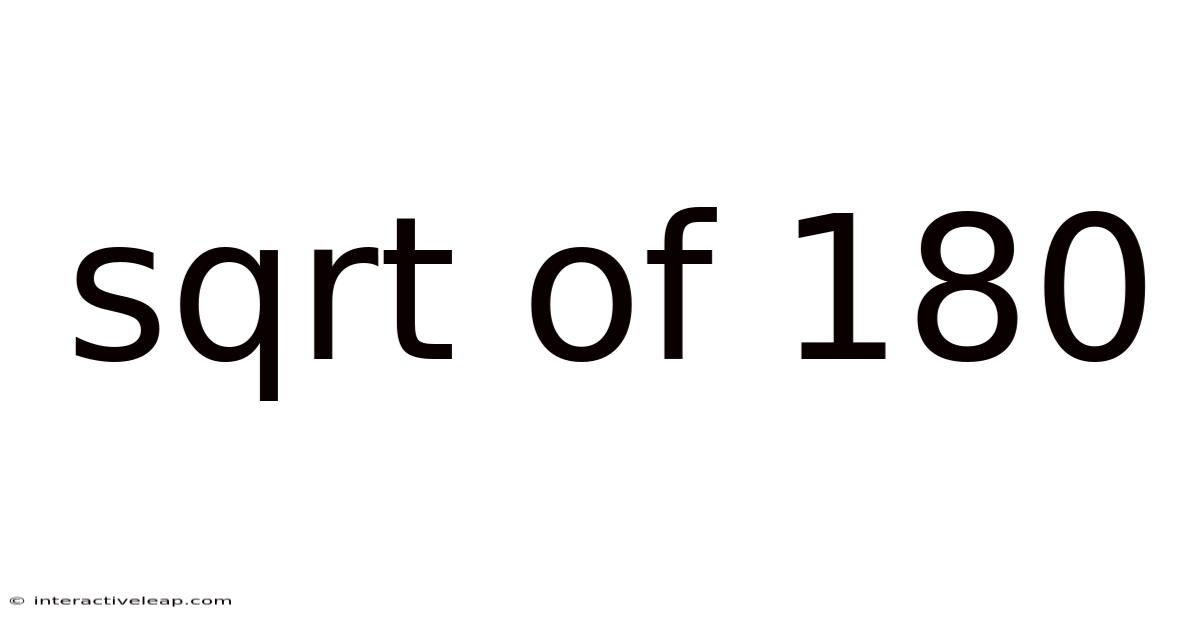
Table of Contents
Unveiling the Mysteries of √180: A Deep Dive into Square Roots and Simplification
Understanding square roots is a fundamental concept in mathematics, crucial for various applications from basic algebra to advanced calculus. This article will explore the square root of 180 (√180), guiding you through the process of simplification and providing a deeper understanding of the underlying mathematical principles. We'll delve into the methods, explain the logic behind each step, and address frequently asked questions to ensure a comprehensive grasp of the topic. By the end, you'll not only know the simplified form of √180 but also possess a robust understanding of square root simplification techniques.
Understanding Square Roots
Before we tackle √180, let's solidify our understanding of square roots. A square root of a number x is a value that, when multiplied by itself, equals x. For instance, the square root of 9 (√9) is 3 because 3 x 3 = 9. The symbol '√' is called the radical symbol, and the number inside is called the radicand.
Not all numbers have perfect square roots (i.e., integer solutions). Numbers like 2, 3, 5, etc., have irrational square roots, meaning their decimal representation goes on forever without repeating. However, we can often simplify these irrational square roots to a more manageable form.
Simplifying √180: A Step-by-Step Guide
Simplifying √180 involves finding the largest perfect square that is a factor of 180. Perfect squares are numbers that result from squaring an integer (e.g., 1, 4, 9, 16, 25, 36, and so on).
Here's how we simplify √180:
-
Find the Prime Factorization: The first step is to find the prime factorization of 180. Prime factorization is expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
180 = 2 x 90 = 2 x 2 x 45 = 2 x 2 x 3 x 15 = 2 x 2 x 3 x 3 x 5 = 2² x 3² x 5
-
Identify Perfect Squares: Now, examine the prime factorization. We see that we have 2² and 3². These are perfect squares because 2 x 2 = 4 and 3 x 3 = 9.
-
Rewrite using Perfect Squares: Rewrite the expression using these perfect squares:
√180 = √(2² x 3² x 5)
-
Apply the Product Rule for Radicals: The product rule for radicals states that √(a x b) = √a x √b. We can use this rule to separate the perfect squares:
√(2² x 3² x 5) = √2² x √3² x √5
-
Simplify Perfect Squares: The square root of a perfect square is simply the integer that was squared. Therefore:
√2² = 2 and √3² = 3
-
Final Simplified Form: Substitute these values back into the expression:
√180 = 2 x 3 x √5 = 6√5
Therefore, the simplified form of √180 is 6√5. This is the most accurate and concise representation of the square root of 180.
The Significance of Simplification
Simplifying square roots is not merely an exercise in mathematical manipulation; it serves several important purposes:
-
Clarity and Conciseness: The simplified form (6√5) is much clearer and easier to understand than the original form (√180). It allows for easier comparison and calculation in more complex equations.
-
Efficiency in Calculations: Simplifying before performing further calculations can drastically reduce computational complexity, preventing errors and saving time. Imagine needing to use √180 in a longer equation; working with 6√5 will be far more efficient.
-
Standard Form: Presenting answers in simplified form is a standard practice in mathematics. It reflects mathematical precision and consistency.
Understanding Irrational Numbers
The simplified form of √180, 6√5, highlights the concept of irrational numbers. √5 is an irrational number, meaning it cannot be expressed as a fraction of two integers. Its decimal representation is non-terminating and non-repeating (approximately 2.236). However, simplifying the square root helps manage this irrationality by isolating the irrational part (√5) from the rational part (6).
Alternative Methods for Simplification
While the prime factorization method is the most systematic approach, other methods can also be used to simplify square roots, although they may require more intuition and trial-and-error:
-
Identifying Factors: You can try identifying perfect square factors directly. For example, you might recognize that 180 is divisible by 36 (a perfect square), leading to: √180 = √(36 x 5) = √36 x √5 = 6√5.
-
Repeated Division: This method involves repeatedly dividing the radicand by perfect squares until no more perfect square factors remain. For instance, you could divide 180 by 4 (2²), resulting in 45. Then divide 45 by 9 (3²), leaving 5. This gives us √180 = √(4 x 9 x 5) = 2 x 3 x √5 = 6√5.
Further Exploration: Applications of Square Roots
Square roots have a wide range of applications across numerous fields:
-
Geometry: Calculating the lengths of sides in right-angled triangles using the Pythagorean theorem (a² + b² = c²) heavily relies on square roots.
-
Physics: Many physical phenomena involve square roots, from calculating the speed of objects to understanding the relationships between forces and energy.
-
Engineering: Square roots are essential in structural design, electrical engineering, and numerous other engineering disciplines.
-
Computer Graphics: Square roots are fundamental in computer graphics for transformations, distance calculations, and vector operations.
-
Statistics: Standard deviation, a crucial measure of data dispersion, involves square roots.
Frequently Asked Questions (FAQs)
-
Q: Is there only one way to simplify a square root?
A: No, there might be multiple ways, but they should all lead to the same simplified form. The prime factorization method provides a systematic approach, reducing the chance of error.
-
Q: What if the radicand is negative?
A: The square root of a negative number is an imaginary number, represented using the imaginary unit i, where i² = -1. For example, √-9 = 3i.
-
Q: How do I handle square roots in more complex expressions?
A: The principles of simplification remain the same. Simplify each individual square root before performing other operations. Remember to follow the order of operations (PEMDAS/BODMAS).
-
Q: Can I use a calculator to find the square root?
A: Yes, calculators can provide decimal approximations of square roots. However, understanding how to simplify square roots is crucial for grasping the underlying mathematical concepts and for solving problems that require exact answers rather than approximations.
Conclusion
Understanding and simplifying square roots, as illustrated with the example of √180, is a cornerstone of mathematical proficiency. Mastering the techniques discussed—prime factorization and application of the product rule—empowers you to tackle more complex problems effectively and efficiently. The process isn’t just about obtaining an answer; it’s about understanding the underlying mathematical principles and their diverse applications in various fields. By mastering this fundamental skill, you build a strong foundation for more advanced mathematical concepts. Remember, the beauty of mathematics lies not just in the answers but in the journey of discovery and understanding. So continue exploring, practicing, and deepening your understanding—the rewards are endless!
Latest Posts
Latest Posts
-
1000 In Pounds
Sep 23, 2025
-
18kh In Stone
Sep 23, 2025
-
36 100 Simplified
Sep 23, 2025
-
Juli Baker Flipped
Sep 23, 2025
-
50feet To Meters
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Sqrt Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.