Simplify 21 28
interactiveleap
Sep 19, 2025 · 6 min read
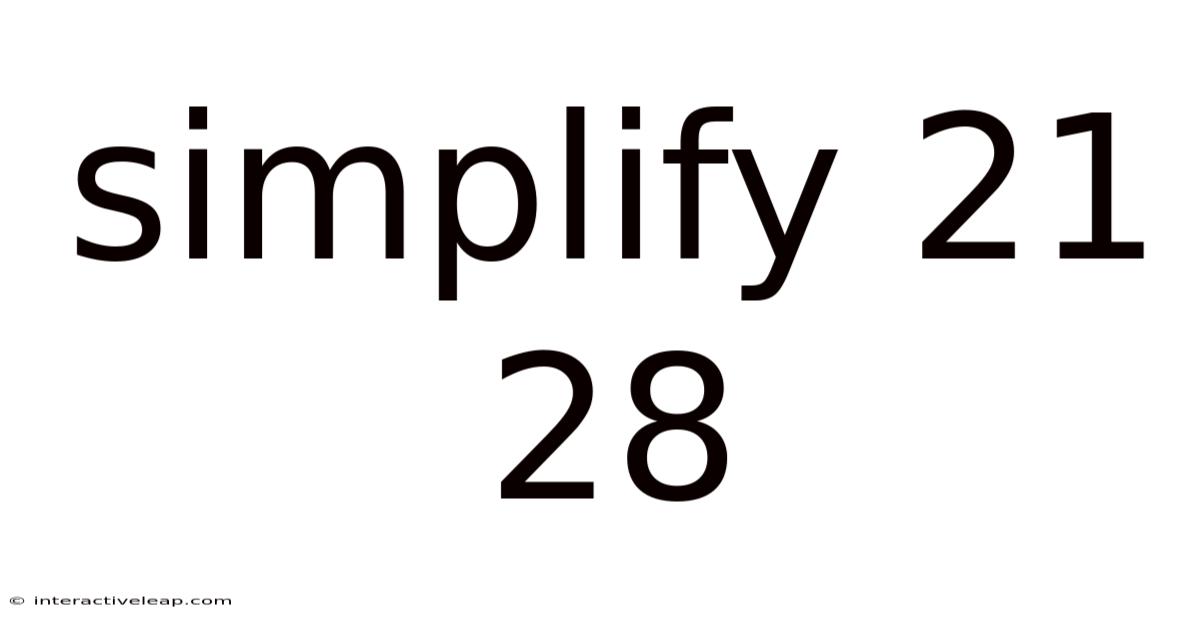
Table of Contents
Simplifying 21/28: A Comprehensive Guide to Fraction Reduction
Understanding how to simplify fractions is a fundamental skill in mathematics, crucial for everything from basic arithmetic to advanced calculus. This comprehensive guide will walk you through the process of simplifying the fraction 21/28, explaining the underlying concepts and providing practical examples to solidify your understanding. We'll explore different methods, including finding the greatest common divisor (GCD), and address common questions and misconceptions. By the end, you'll not only know the simplified form of 21/28 but also possess the tools to simplify any fraction with confidence.
Introduction: Understanding Fraction Simplification
A fraction represents a part of a whole. It's written as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). Simplifying a fraction, also known as reducing a fraction, means expressing it in its simplest form. This means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. This makes the fraction easier to understand and work with in calculations. Simplifying 21/28 involves finding the greatest common divisor (GCD) of 21 and 28 and then dividing both the numerator and the denominator by that GCD.
Method 1: Finding the Greatest Common Divisor (GCD)
The most efficient way to simplify a fraction is by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both numbers without leaving a remainder. There are several ways to find the GCD:
-
Listing Factors: List all the factors of both the numerator (21) and the denominator (28). The largest number that appears in both lists is the GCD.
Factors of 21: 1, 3, 7, 21 Factors of 28: 1, 2, 4, 7, 14, 28
The largest common factor is 7.
-
Prime Factorization: Break down both numbers into their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
21 = 3 x 7 28 = 2 x 2 x 7 = 2² x 7
The common prime factor is 7. Therefore, the GCD is 7.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 28 by 21: 28 = 21 x 1 + 7
- Divide 21 by the remainder 7: 21 = 7 x 3 + 0
The last non-zero remainder is 7, so the GCD is 7.
Simplifying 21/28 using the GCD
Now that we've established that the GCD of 21 and 28 is 7, we can simplify the fraction:
21/28 = (21 ÷ 7) / (28 ÷ 7) = 3/4
Therefore, the simplified form of 21/28 is 3/4.
Method 2: Step-by-Step Simplification (without explicitly finding the GCD)
While finding the GCD is the most efficient method, you can also simplify a fraction by repeatedly dividing both the numerator and denominator by common factors until no more common factors exist. This method might take longer, but it's a good approach for building intuition.
-
Identify a common factor: Notice that both 21 and 28 are divisible by 7.
-
Divide both numerator and denominator by the common factor:
21/28 = (21 ÷ 7) / (28 ÷ 7) = 3/4
-
Check for further common factors: 3 and 4 have no common factors other than 1. Therefore, the fraction is simplified.
The result, again, is 3/4.
Visual Representation: Understanding the Equivalence
It's helpful to visualize what simplification means. Imagine you have a pizza cut into 28 slices. The fraction 21/28 represents 21 of these slices. Simplifying to 3/4 means grouping the slices. You can group the 28 slices into 4 equal groups of 7 slices each. Then, 21 slices correspond to 3 of these groups. This visually demonstrates that 21/28 and 3/4 represent the same portion of the whole pizza.
Explanation with Scientific Principles
The process of simplifying fractions aligns with fundamental mathematical principles:
-
Equivalence Relations: Simplifying a fraction doesn't change its value; it merely expresses it in a different but equivalent form. This is based on the concept of equivalence relations in mathematics, where elements are considered equivalent if they share a specific property (in this case, representing the same proportion).
-
Divisibility Rules: Understanding divisibility rules (rules for determining if a number is divisible by another number without performing the division) can help speed up the simplification process. For example, knowing that both 21 and 28 are divisible by 7 allows for quick simplification.
-
Prime Factorization Theorem: The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be uniquely represented as a product of prime numbers. This theorem underpins the prime factorization method for finding the GCD, which is a powerful tool in number theory and beyond.
Frequently Asked Questions (FAQ)
Q: What if I don't know the GCD immediately?
A: Don't worry! You can use the step-by-step method or the Euclidean algorithm. Start with any common factor you see, and keep simplifying until you reach the simplest form.
Q: Can a fraction be simplified more than once?
A: Yes, sometimes you might need to divide by multiple common factors to fully simplify the fraction. However, once you reach a point where the numerator and denominator share no common factors other than 1, you know it's in its simplest form.
Q: Is there a way to check my answer?
A: Yes! You can check your answer by multiplying both the numerator and the denominator of the simplified fraction by the GCD. If you get back to the original fraction, your simplification is correct. For example, 3/4 x 7/7 = 21/28.
Q: What happens if the GCD is 1?
A: If the GCD of the numerator and denominator is 1, then the fraction is already in its simplest form. It cannot be simplified further.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand and work with in calculations. It also allows for easier comparisons between fractions and facilitates more efficient problem-solving in various mathematical contexts.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill with applications across numerous mathematical concepts. Understanding the various methods for finding the GCD, such as listing factors, prime factorization, and the Euclidean algorithm, empowers you to efficiently simplify any fraction. Remember that the key is to find the greatest common divisor of the numerator and denominator and divide both by it. By mastering this skill, you build a strong foundation for more advanced mathematical studies and problem-solving. The simplification of 21/28 to 3/4 is not just a simple calculation; it’s a demonstration of the underlying principles of equivalence, divisibility, and the fundamental theorem of arithmetic. Practice regularly, and soon you'll be simplifying fractions with ease and confidence.
Latest Posts
Latest Posts
-
Lady Macbeth Outfit
Sep 19, 2025
-
Purple Blue Pink
Sep 19, 2025
-
47 In Pounds
Sep 19, 2025
-
102cm In Inches
Sep 19, 2025
-
Cubits To Meters
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Simplify 21 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.