Simplify 14 30
interactiveleap
Sep 21, 2025 · 5 min read
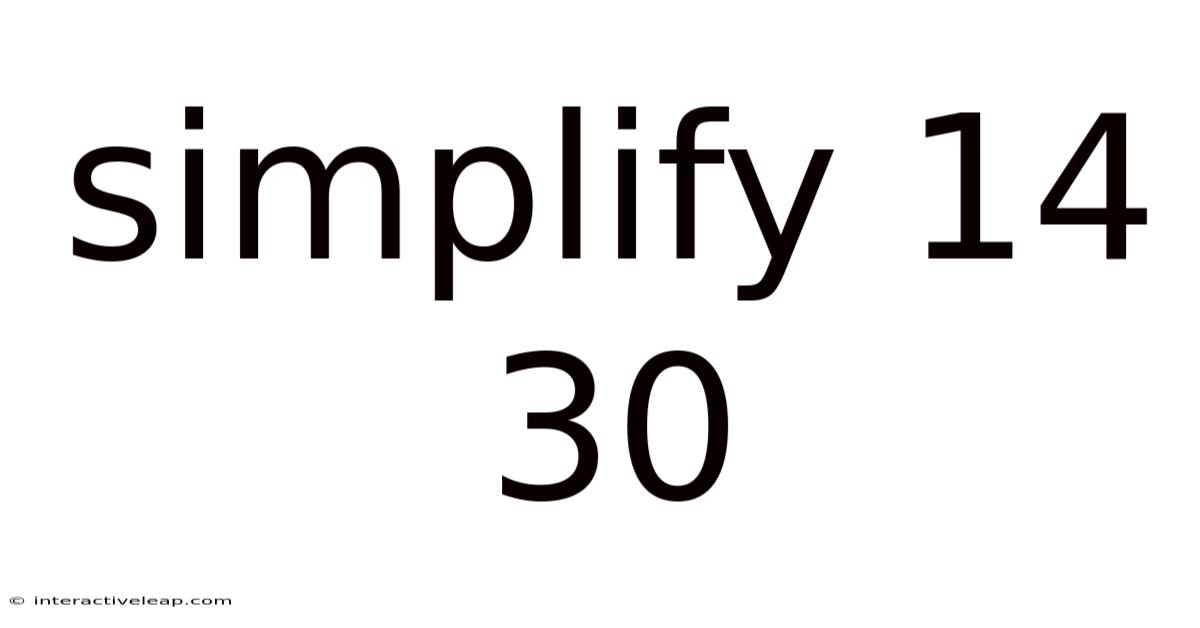
Table of Contents
Simplifying Fractions: A Deep Dive into 14/30
Simplifying fractions is a fundamental concept in mathematics, crucial for understanding more advanced topics like algebra and calculus. This article will provide a comprehensive guide on simplifying fractions, using the example of 14/30. We will explore the concept in detail, explaining the process step-by-step, providing the underlying mathematical reasoning, and addressing frequently asked questions. By the end, you'll not only know how to simplify 14/30 but also understand the broader principles of fraction simplification. This will equip you with the skills to tackle any fraction simplification problem you encounter.
Understanding Fractions
Before diving into simplification, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's written in the form a/b, where 'a' is the numerator (the top number) and 'b' is the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts we're considering. For example, in the fraction 14/30, the whole is divided into 30 equal parts, and we are considering 14 of those parts.
Simplifying Fractions: The Core Concept
Simplifying a fraction means reducing it to its simplest form, where the numerator and denominator have no common factors other than 1. This doesn't change the value of the fraction; it just represents it in a more concise and manageable way. Think of it like reducing a recipe – you can halve or quarter all the ingredients without changing the final dish. Similarly, simplifying a fraction doesn't alter its value, only its appearance.
Step-by-Step Simplification of 14/30
To simplify 14/30, we need to find the greatest common divisor (GCD) of 14 and 30. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. There are several ways to find the GCD:
1. Listing Factors:
- Factors of 14: 1, 2, 7, 14
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
The largest number that appears in both lists is 2. Therefore, the GCD of 14 and 30 is 2.
2. Prime Factorization:
This method is particularly useful for larger numbers. We break down each number into its prime factors (numbers divisible only by 1 and themselves):
- 14 = 2 x 7
- 30 = 2 x 3 x 5
The common prime factor is 2. Therefore, the GCD is 2.
3. Euclidean Algorithm:
This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 30 by 14: 30 = 14 x 2 + 2
- Divide 14 by the remainder 2: 14 = 2 x 7 + 0
The last non-zero remainder is 2, so the GCD is 2.
Now that we've found the GCD (2), we can simplify the fraction:
14/30 = (14 ÷ 2) / (30 ÷ 2) = 7/15
Therefore, the simplified form of 14/30 is 7/15.
Visualizing Fraction Simplification
Imagine a pizza cut into 30 slices. You have 14 slices (14/30). If you group the slices into pairs (because the GCD is 2), you'll have 7 pairs of slices out of a total of 15 pairs. This visually represents the simplified fraction 7/15. The pizza's size remains the same; only the grouping of the slices has changed.
Further Exploration: Simplifying Fractions with Larger Numbers
The methods described above are applicable to any fraction. Let's consider a more complex example: simplify 105/135.
-
Find the GCD: Using prime factorization:
- 105 = 3 x 5 x 7
- 135 = 3 x 3 x 3 x 5 = 3³ x 5
The common factors are 3 and 5. Therefore, the GCD is 3 x 5 = 15.
-
Simplify the Fraction:
105/135 = (105 ÷ 15) / (135 ÷ 15) = 7/9
Therefore, the simplified form of 105/135 is 7/9.
The Importance of Simplifying Fractions
Simplifying fractions is not just about aesthetics; it's crucial for several reasons:
- Clarity: Simplified fractions are easier to understand and work with. 7/15 is much clearer than 14/30.
- Accuracy: Simplified fractions reduce the risk of errors in calculations, especially when dealing with more complex operations.
- Efficiency: Simplified fractions make calculations faster and more efficient.
- Comparison: It's easier to compare simplified fractions. For example, comparing 7/15 and 2/5 is simpler than comparing 14/30 and 12/30.
Frequently Asked Questions (FAQ)
Q1: What if the numerator is 1? Can the fraction be simplified further?
A1: If the numerator is 1, the fraction is already in its simplest form. For example, 1/5 cannot be simplified further.
Q2: What if the GCD is 1?
A2: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form and cannot be simplified further. This means that the numerator and denominator share no common factors other than 1.
Q3: Can I simplify fractions with negative numbers?
A3: Yes. The simplification process remains the same. For example, -14/30 simplifies to -7/15. The negative sign remains unchanged.
Q4: Are there any shortcuts for simplifying fractions?
A4: While there are no magic shortcuts, familiarity with divisibility rules (e.g., a number is divisible by 2 if it's even, by 3 if the sum of its digits is divisible by 3, etc.) can speed up the process of finding the GCD. Practice makes perfect!
Conclusion
Simplifying fractions is a fundamental skill in mathematics with far-reaching applications. Mastering this concept allows for clearer understanding, more efficient calculations, and reduced error rates in further mathematical studies. By understanding the process, whether through listing factors, prime factorization, or the Euclidean algorithm, and by practicing consistently, you will develop a strong foundation in this essential mathematical skill. Remember, the key is to find the greatest common divisor of the numerator and denominator and then divide both by that number. This simple process transforms complex fractions into their simplest and most manageable forms. Through the detailed explanation and examples provided, you should now confidently simplify any fraction you encounter, starting with the fundamental example of 14/30 and expanding to more complex scenarios.
Latest Posts
Latest Posts
-
A 3 2
Sep 21, 2025
-
Amable In English
Sep 21, 2025
-
Cities In Philippines
Sep 21, 2025
-
12 3 4
Sep 21, 2025
-
120f To C
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Simplify 14 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.