Factorise 5x 10
interactiveleap
Sep 17, 2025 · 5 min read
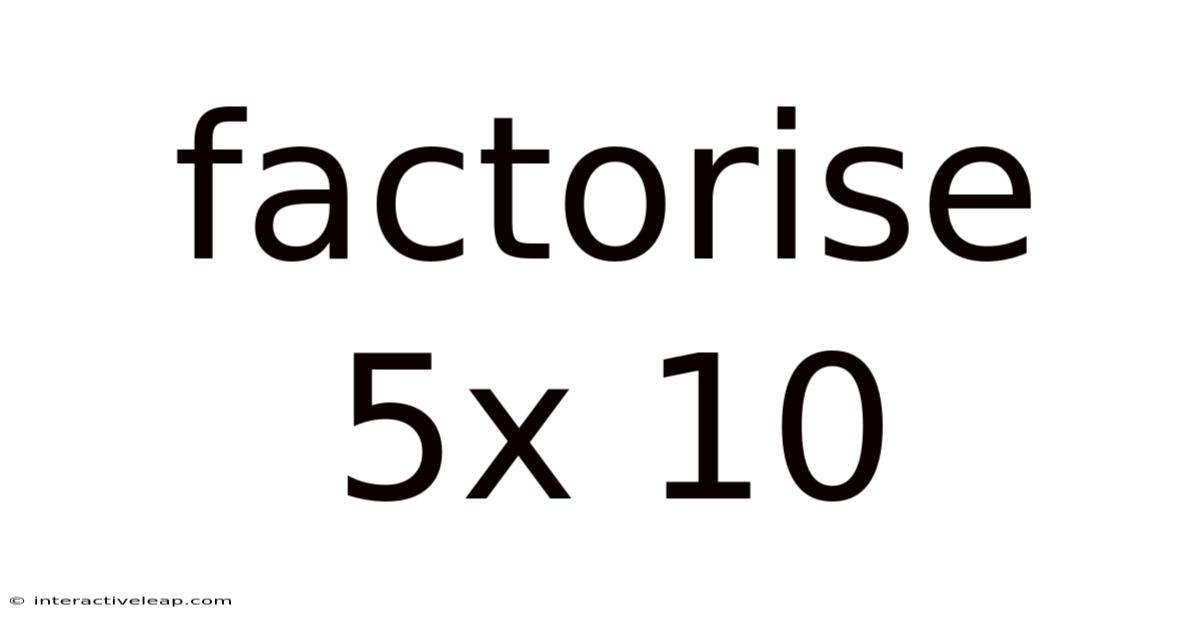
Table of Contents
Factorising 5x + 10: A Comprehensive Guide
This article provides a detailed explanation of how to factorise the algebraic expression 5x + 10. We will cover the fundamental concepts of factorisation, demonstrate the steps involved, and delve into the underlying mathematical principles. This guide is designed for learners of all levels, from beginners grasping the basics to those seeking a deeper understanding of algebraic manipulation. Understanding factorisation is crucial for progressing in algebra and many related fields like calculus and beyond.
Understanding Factorisation
Factorisation, in its simplest form, is the process of breaking down a mathematical expression into smaller parts, or factors, that when multiplied together, produce the original expression. Think of it like reverse multiplication. Just as 2 x 5 = 10, factorising 10 gives you the factors 2 and 5. In algebra, we apply this same principle to expressions containing variables (like 'x').
The goal of factorisation is to simplify expressions, making them easier to work with in more complex calculations, such as solving equations or simplifying fractions. It's a fundamental skill used extensively throughout mathematics.
Step-by-Step Factorisation of 5x + 10
Let's break down the factorisation of 5x + 10 step-by-step:
1. Identify the Common Factor:
The first step in factorising any expression is to identify the highest common factor (HCF) of all the terms. In the expression 5x + 10, we have two terms: 5x and 10. Let's find their common factors.
- 5x: The factors are 5 and x.
- 10: The factors are 2, 5, and 10.
The highest common factor of 5x and 10 is 5.
2. Factor out the Common Factor:
Once we've identified the HCF (5), we factor it out from both terms. This means we divide each term by the HCF and place the HCF outside a pair of parentheses:
5x + 10 = 5(x + 2)
Let's verify this: If we expand 5(x + 2), we get 5 * x + 5 * 2 = 5x + 10 – the original expression. This confirms our factorisation is correct.
Explanation of the Mathematical Principles
The process we followed relies on the distributive property of multiplication over addition. The distributive property states that a(b + c) = ab + ac. In our case, a = 5, b = x, and c = 2. By factoring out the 5, we are essentially applying the distributive property in reverse.
This seemingly simple concept has far-reaching implications in algebra and beyond. It forms the basis for many advanced algebraic manipulations and is essential for simplifying complex expressions and solving equations.
Further Exploration: More Complex Factorisation
While 5x + 10 is a relatively simple example, the principles of factorisation extend to more complex expressions. Let's consider some variations and explore the underlying concepts in more detail:
1. Factorising Expressions with Negative Terms:
Consider the expression -3x - 9. The HCF here is -3. Factoring this out:
-3x - 9 = -3(x + 3)
Notice that we factored out a negative sign. This is crucial to ensure the terms within the parentheses have the correct signs. Always carefully check your work by expanding the factorised expression to verify the result.
2. Factorising Trinomials:
Trinomials are algebraic expressions with three terms. Factorising trinomials is more complex and often requires a bit more trial and error, or specific techniques like the quadratic formula (for quadratic trinomials). For example:
x² + 5x + 6 can be factorised as (x + 2)(x + 3)
This example involves finding two numbers that add up to 5 (the coefficient of x) and multiply to 6 (the constant term). The techniques for factoring trinomials are more advanced and deserve their own comprehensive discussion.
3. Factorising Expressions with Higher Powers:
Factorisation extends to expressions with variables raised to higher powers (e.g., x³, x⁴). These often involve more sophisticated techniques, including the use of grouping and the difference of squares or cubes. For example:
x³ - 8 can be factorised as (x - 2)(x² + 2x + 4).
This relies on recognizing the difference of cubes formula: a³ - b³ = (a - b)(a² + ab + b²).
Frequently Asked Questions (FAQ)
Q1: Why is factorisation important?
A1: Factorisation is a cornerstone of algebra. It simplifies complex expressions, making them easier to manipulate in various mathematical operations, such as solving equations, simplifying fractions, and performing calculus. It's a building block for more advanced mathematical concepts.
Q2: What if I can't find a common factor?
A2: If you can't find a common factor among all terms, the expression might be a prime expression (meaning it can't be factored further using integer coefficients). However, this is not always the case, especially with more complex expressions. More advanced techniques might be needed.
Q3: Are there different methods for factorisation?
A3: Yes, there are several methods for factorisation, depending on the type of expression. These include:
- Greatest Common Factor (GCF) method: This is the method we used for 5x + 10, focusing on finding and extracting the highest common factor.
- Grouping method: Used for expressions with four or more terms, often involving grouping terms with common factors.
- Difference of squares: Used for expressions of the form a² - b².
- Sum and difference of cubes: Used for expressions of the form a³ + b³ and a³ - b³.
- Quadratic formula: Used to factorise quadratic trinomials.
Q4: How can I practice factorisation?
A4: The best way to practice factorisation is through consistent exercise. Start with simple expressions like 5x + 10 and gradually work your way up to more complex examples. Plenty of online resources and textbooks offer practice problems and explanations. The key is to understand the underlying principles and apply them systematically.
Conclusion
Factorising algebraic expressions, as demonstrated through the example of 5x + 10, is a fundamental skill in algebra and beyond. While this particular example was straightforward, mastering the underlying principles of identifying common factors and applying the distributive property is crucial for tackling more challenging problems. Consistent practice and a clear understanding of the mathematical concepts will empower you to confidently handle various factorisation techniques and further your mathematical journey. Remember to always check your work by expanding your factorised expression to ensure it matches the original expression. This will build confidence and reinforce your understanding of the process. Good luck with your factorisation practice!
Latest Posts
Latest Posts
-
Factor 5x 10
Sep 17, 2025
-
Merry Cone Spanish
Sep 17, 2025
-
9 Times 4
Sep 17, 2025
-
235 Kph Mph
Sep 17, 2025
-
Calcium Hydrochloric Acid
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Factorise 5x 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.