Factorise 2x 10
interactiveleap
Sep 14, 2025 · 5 min read
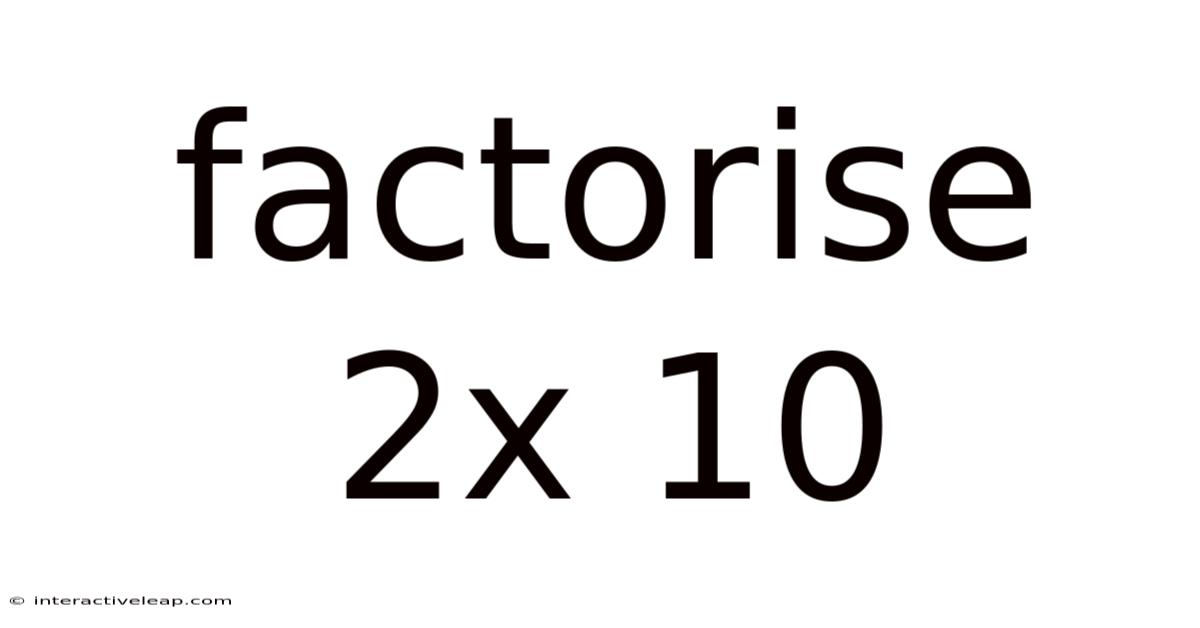
Table of Contents
Factorising 2x + 10: A Comprehensive Guide
This article provides a comprehensive guide to factorising the algebraic expression 2x + 10. We will explore various methods, explain the underlying principles, and delve into the broader context of factorisation in algebra. Understanding factorisation is crucial for simplifying expressions, solving equations, and progressing to more advanced algebraic concepts. This guide is designed for students of all levels, from those just beginning their algebraic journey to those looking to solidify their understanding.
Introduction to Factorisation
Factorisation, in its simplest form, is the process of breaking down an algebraic expression into smaller, simpler expressions that, when multiplied together, result in the original expression. Think of it like reverse multiplication. Just as you can multiply numbers together (e.g., 2 x 5 = 10), factorisation involves finding the numbers or expressions that, when multiplied, give you the original number or expression. In the case of 2x + 10, we are looking for the factors that, when multiplied, give us this binomial expression.
Method 1: Finding the Greatest Common Factor (GCF)
The most straightforward method for factorising 2x + 10 involves identifying the greatest common factor (GCF) of the terms. The GCF is the largest number or expression that divides evenly into both terms without leaving a remainder.
Let's examine the terms in 2x + 10:
- 2x: The terms are 2 and x.
- 10: The factors are 1, 2, 5, and 10.
By comparing the factors of each term, we see that the greatest common factor is 2.
Now, we can factor out the GCF (2) from both terms:
2x + 10 = 2(x + 5)
This is the factorised form of 2x + 10. We can verify this by expanding the factorised expression: 2(x + 5) = 2x + 10. The result matches the original expression, confirming that our factorisation is correct.
Method 2: Using the Distributive Property
The distributive property, also known as the distributive law, is a fundamental concept in algebra. It states that a(b + c) = ab + ac. We can use this property in reverse to factorise expressions.
Observe the expression 2x + 10. We can rewrite it as:
2x + 10 = 2 * x + 2 * 5
Notice that the number 2 is a common factor in both terms. Applying the distributive property in reverse, we can factor out the 2:
2 * x + 2 * 5 = 2(x + 5)
Again, we arrive at the factorised form 2(x + 5). This method reinforces the importance of the distributive property in the context of factorisation.
Understanding the Factors
The factorised expression 2(x + 5) reveals the factors of 2x + 10:
- 2: This is a numerical factor.
- (x + 5): This is an algebraic factor, a binomial expression.
Both factors, when multiplied, yield the original expression 2x + 10. This decomposition into factors is crucial for further algebraic manipulations and problem-solving.
Applications of Factorisation
The ability to factorise algebraic expressions is essential for various algebraic operations and problem-solving techniques. Some key applications include:
-
Solving Quadratic Equations: Factorisation is a fundamental tool for solving quadratic equations (equations of the form ax² + bx + c = 0). By factorising the quadratic expression, we can find the roots (solutions) of the equation.
-
Simplifying Expressions: Factorisation simplifies complex expressions, making them easier to understand and manipulate. This simplification is crucial for performing other algebraic operations, such as adding, subtracting, multiplying, and dividing expressions.
-
Cancelling Common Factors: In fractions involving algebraic expressions, factorisation allows us to cancel common factors in the numerator and denominator, simplifying the fraction to its lowest terms.
-
Graphing Quadratic Functions: Factorising a quadratic function helps in identifying the x-intercepts (where the graph crosses the x-axis) which provides valuable information about the graph's shape and properties.
Further Exploration: Factorising More Complex Expressions
While 2x + 10 is a relatively simple expression to factorise, the principles discussed here can be extended to more complex expressions. For example:
-
Expressions with more terms: Expressions containing three or more terms may require different techniques, such as grouping or factoring by grouping. This involves grouping terms with common factors together before factoring out the GCF of each group.
-
Expressions with higher powers: Expressions involving higher powers of x (e.g., x², x³, etc.) will often require more advanced factorisation techniques, such as the difference of squares, sum and difference of cubes, or using the quadratic formula.
Frequently Asked Questions (FAQs)
Q: What if the expression doesn't have a common factor?
A: If the terms in an expression don't share a common factor other than 1, the expression is considered prime and cannot be further factorised using the methods described above. However, other techniques might apply depending on the structure of the expression.
Q: Is there only one way to factorise an expression?
A: For expressions like 2x + 10, the factorisation 2(x + 5) is essentially unique. However, for more complex expressions, there might be different ways to factorise, but they will all represent equivalent forms of the original expression. The order of factors might be different, but the overall result after expansion should be the same.
Q: What happens if I make a mistake while factorising?
A: Always check your work by expanding the factorised expression. If the expanded expression matches the original expression, your factorisation is correct. If not, carefully review your steps to identify where the error occurred.
Q: Why is factorisation important in higher-level mathematics?
A: Factorisation is a fundamental skill that forms the basis for many advanced mathematical concepts. It's crucial for calculus, linear algebra, and other areas of higher mathematics. Proficiency in factorisation significantly simplifies complex mathematical problems.
Conclusion
Factorising algebraic expressions, even seemingly simple ones like 2x + 10, is a fundamental skill in algebra. Mastering this skill is crucial for success in further mathematical studies. By understanding the concepts of the greatest common factor and the distributive property, you can confidently factorise a wide range of expressions. Remember to practice regularly and always check your work to ensure accuracy. The ability to efficiently and accurately factorise expressions will significantly enhance your problem-solving skills and prepare you for more complex algebraic challenges. Consistent practice and a clear understanding of the underlying principles will transform this seemingly simple concept into a powerful tool in your mathematical arsenal. Don't hesitate to revisit these steps and explore additional resources to solidify your understanding of factorisation. With dedicated practice, you'll become proficient in this essential algebraic technique.
Latest Posts
Latest Posts
-
62lb In Stone
Sep 14, 2025
-
Latitude Montreal Canada
Sep 14, 2025
-
45km To Miles
Sep 14, 2025
-
North East Landmarks
Sep 14, 2025
-
97lbs To Stone
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Factorise 2x 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.