Cos Of 2pi/3
interactiveleap
Sep 23, 2025 · 5 min read
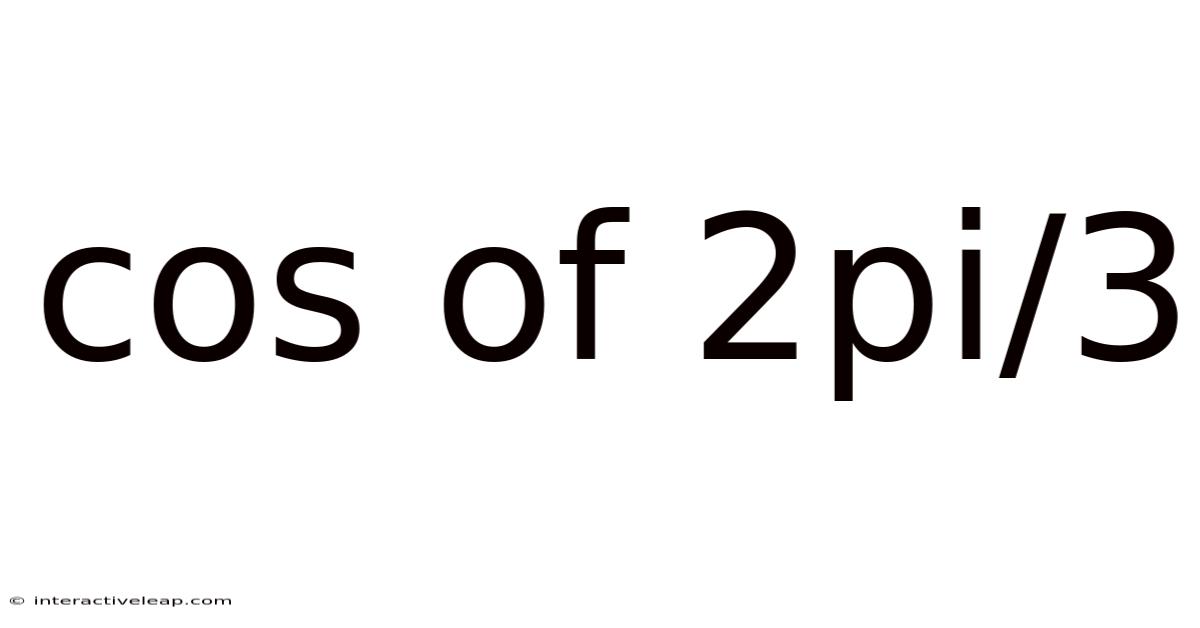
Table of Contents
Unveiling the Mystery: A Deep Dive into cos(2π/3)
Understanding trigonometric functions like cosine is fundamental in mathematics, physics, and engineering. This article provides a comprehensive exploration of cos(2π/3), explaining its value, derivation methods, applications, and related concepts. We'll cover various approaches, from using the unit circle to leveraging trigonometric identities, ensuring a thorough understanding for readers of all levels. This in-depth guide will equip you with the knowledge to confidently handle similar trigonometric problems.
Introduction: Understanding the Angle 2π/3
The expression cos(2π/3) refers to the cosine of an angle measuring 2π/3 radians. Radians are a unit of angular measurement, with 2π radians equivalent to 360 degrees (a full circle). Therefore, 2π/3 radians represents (2π/3) * (180/π) = 120 degrees. This angle lies in the second quadrant of the Cartesian coordinate system. Understanding the quadrant is crucial because it determines the sign of the cosine function. In the second quadrant, cosine is negative.
Method 1: Using the Unit Circle
The unit circle provides a visual and intuitive method to determine the cosine of any angle. The unit circle is a circle with a radius of 1 centered at the origin (0,0) of the Cartesian plane. Any point on the unit circle can be represented by its coordinates (cos θ, sin θ), where θ is the angle formed between the positive x-axis and the line connecting the origin to that point.
To find cos(2π/3), we locate the point on the unit circle corresponding to an angle of 120 degrees (or 2π/3 radians). This point lies in the second quadrant. By symmetry, the x-coordinate of this point is the negative of the x-coordinate of the point representing 60 degrees (π/3 radians). Since cos(π/3) = 1/2, cos(2π/3) = -1/2.
Method 2: Utilizing Trigonometric Identities
Several trigonometric identities can help us calculate cos(2π/3). One useful identity is the cosine of a sum:
cos(A + B) = cos A cos B - sin A sin B
We can express 2π/3 as π/3 + π/3. Therefore:
cos(2π/3) = cos(π/3 + π/3) = cos(π/3)cos(π/3) - sin(π/3)sin(π/3)
Substituting the known values cos(π/3) = 1/2 and sin(π/3) = √3/2:
cos(2π/3) = (1/2)(1/2) - (√3/2)(√3/2) = 1/4 - 3/4 = -1/2
Another approach involves using the identity:
cos(π - x) = -cos(x)
Since 2π/3 = π - π/3, we have:
cos(2π/3) = cos(π - π/3) = -cos(π/3) = -(1/2) = -1/2
This method highlights the relationship between angles in different quadrants.
Method 3: Employing the Sum-to-Product Formulae
While less direct for this specific calculation, the sum-to-product formulae offer a more general approach to solving trigonometric equations and identities. These are particularly useful when dealing with sums or differences of cosine functions. Though not the most efficient method for cos(2π/3), understanding these formulae expands your trigonometric toolkit.
For example, the formula:
cos x + cos y = 2 cos((x+y)/2) cos((x-y)/2)
can be manipulated (though not straightforwardly in this instance) to find the cosine of specific angles. Similar formulae exist for the sum and difference of sine and cosine functions.
Visual Representation: Graphing the Cosine Function
Graphing the cosine function, y = cos(x), visually confirms the value of cos(2π/3). The graph oscillates between -1 and 1. By locating the x-value corresponding to x = 2π/3 (approximately 2.09 radians), you can observe that the y-value (the cosine value) is indeed -1/2. This graphical approach provides an intuitive understanding of the function's behavior.
Applications of Cos(2π/3)
The value of cos(2π/3) finds applications in various fields:
-
Physics: In wave phenomena, this value might appear in calculations involving the superposition of waves or in analyzing oscillations. Understanding the phase difference represented by the 120-degree angle is crucial.
-
Engineering: Cosine functions are ubiquitous in electrical engineering, representing alternating currents and voltages. This value would be encountered when analyzing AC circuits with phase shifts.
-
Computer Graphics: In 3D graphics, rotations and transformations often involve trigonometric functions. The cosine value might be part of a rotation matrix.
-
Mathematics: It's a fundamental value used in further trigonometric calculations and the derivation of more complex identities.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between degrees and radians?
A: Degrees and radians are both units of angular measurement. 360 degrees equals 2π radians. Radians are preferred in many mathematical and scientific contexts because they simplify calculations involving angles.
-
Q: Why is cosine negative in the second quadrant?
A: The cosine function represents the x-coordinate of a point on the unit circle. In the second quadrant, the x-coordinates are negative.
-
Q: Can I use a calculator to find cos(2π/3)?
A: Yes, most scientific calculators will provide the value of cos(2π/3) directly. Ensure your calculator is set to radians mode.
-
Q: Are there other methods to calculate cos(2π/3)?
A: While the methods described are the most common and straightforward, other advanced techniques involving complex numbers and series expansions can also be used.
Conclusion: Mastering Cos(2π/3) and Beyond
This in-depth exploration of cos(2π/3) has demonstrated that its value is -1/2. We've explored multiple methods for deriving this value, emphasizing the importance of understanding the unit circle, trigonometric identities, and the behavior of the cosine function in different quadrants. Mastering these concepts forms a solid foundation for tackling more advanced trigonometric problems and applications in various scientific and engineering fields. The understanding of this seemingly simple trigonometric value extends to a deeper grasp of mathematical principles and their practical implementations. Remember to practice these methods and explore related trigonometric concepts to strengthen your mathematical skills. The journey of learning mathematics is continuous, and each solved problem contributes to a broader understanding of the subject.
Latest Posts
Latest Posts
-
Stock Control Systems
Sep 23, 2025
-
Gigantic Or Colossal
Sep 23, 2025
-
128 64 32
Sep 23, 2025
-
120kg In Lb
Sep 23, 2025
-
6 Times 40
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Cos Of 2pi/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.