90 Of 35
interactiveleap
Sep 22, 2025 · 6 min read
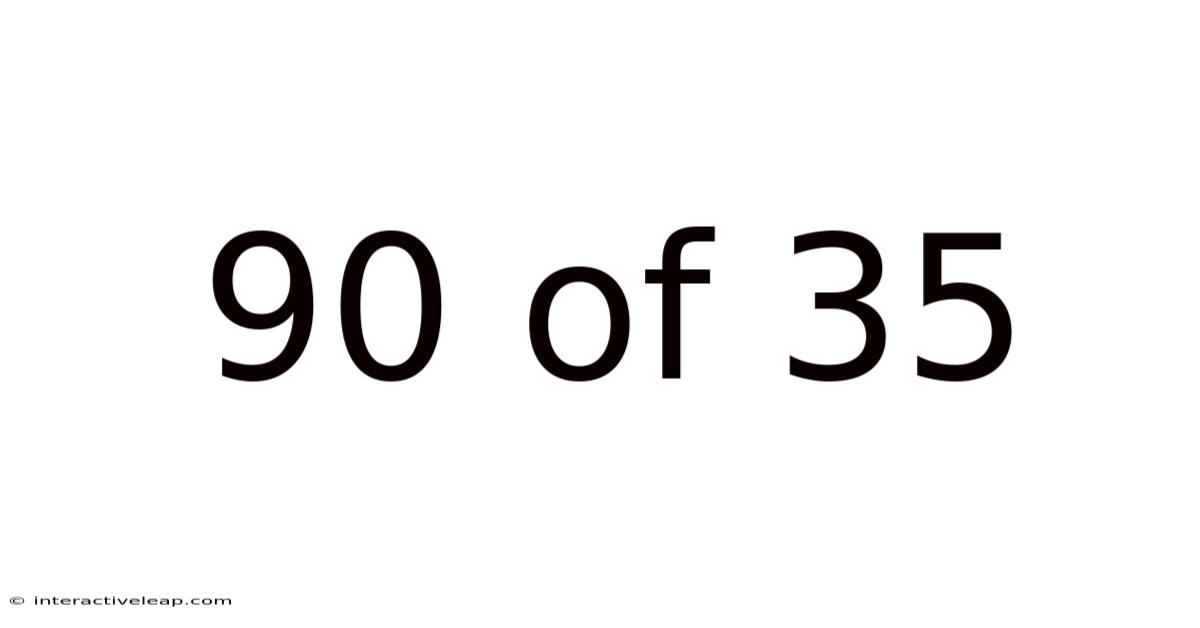
Table of Contents
Decoding 90% of 35: A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to comprehending statistical data and analyzing financial reports. This article will delve into the calculation of 90% of 35, explaining the process step-by-step, exploring the underlying mathematical principles, and highlighting real-world examples where this type of calculation proves invaluable. We will also address common misconceptions and frequently asked questions to ensure a thorough understanding of this seemingly simple yet crucial concept.
Understanding Percentages: A Foundation
Before we tackle the specific problem of finding 90% of 35, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, 90% means 90 out of 100, which can be written as the fraction 90/100 or the decimal 0.9.
This fractional representation is key to understanding percentage calculations. To find a percentage of a number, we multiply the number by the percentage expressed as a decimal. This simple formula forms the basis for all percentage calculations.
Calculating 90% of 35: A Step-by-Step Guide
Now, let's apply this knowledge to find 90% of 35. Following the formula, we perform the following steps:
-
Convert the percentage to a decimal: 90% is equivalent to 0.9 (90 divided by 100).
-
Multiply the number by the decimal: Multiply 35 by 0.9: 35 * 0.9 = 31.5
Therefore, 90% of 35 is 31.5.
This simple calculation can be performed mentally, using a calculator, or even with pen and paper. The key is understanding the underlying principle of converting the percentage to a decimal before multiplication.
Alternative Methods for Calculating Percentages
While the method described above is the most straightforward, there are alternative approaches that can be equally effective, depending on the context and individual preference.
-
Using fractions: As mentioned earlier, 90% can be represented as the fraction 90/100, which simplifies to 9/10. To find 90% of 35, we can multiply 35 by 9/10: 35 * (9/10) = (35 * 9) / 10 = 315 / 10 = 31.5. This method is particularly useful when dealing with simpler percentages that have easily simplified fractional equivalents.
-
Using proportions: We can set up a proportion to solve this problem. We know that 90 is to 100 as x is to 35 (where x represents 90% of 35). This can be written as: 90/100 = x/35. To solve for x, we cross-multiply: 90 * 35 = 100 * x. This simplifies to 3150 = 100x. Dividing both sides by 100 gives us x = 31.5. This method is particularly helpful in understanding the proportional relationships involved.
Real-World Applications: Where Percentages Matter
The ability to calculate percentages is crucial in numerous real-world situations. Here are some examples:
-
Shopping Discounts: Imagine a store offering a 90% discount on an item originally priced at $35. Using our calculation, we know the discount is $31.50, making the final price $3.50 ($35 - $31.50).
-
Tax Calculations: If a sales tax is 9%, calculating the tax amount on a $35 purchase would involve finding 9% of 35, a similar calculation to the one we've performed.
-
Grade Calculations: In many educational systems, final grades are often calculated as a weighted average of different assessment components. Understanding percentages is vital for tracking progress and predicting final grades.
-
Financial Analysis: Percentage changes are frequently used to track financial performance, such as comparing year-over-year revenue growth or analyzing investment returns.
-
Data Analysis: Percentages are essential for interpreting and presenting statistical data. For example, researchers might express the percentage of respondents who agree with a particular statement in a survey.
Addressing Common Misconceptions
Several common misconceptions can hinder a proper understanding of percentage calculations. Let's address some of them:
-
Confusing percentage with the actual value: It's crucial to remember that a percentage represents a portion of a whole, not the whole itself. 90% of 35 is not 90; it's 31.5.
-
Incorrect decimal conversion: A frequent error is making a mistake when converting a percentage to a decimal. Always remember to divide the percentage by 100.
-
Ignoring the order of operations: When dealing with more complex calculations involving percentages and other mathematical operations, it's vital to follow the correct order of operations (PEMDAS/BODMAS).
Expanding the Concept: Beyond 90% of 35
Understanding the calculation of 90% of 35 provides a solid foundation for tackling more complex percentage problems. The core principle remains the same: convert the percentage to a decimal and multiply by the given number. You can apply this principle to calculate any percentage of any number. For example, finding 37% of 125, or 1.5% of 800, would follow the same fundamental steps.
The ability to handle percentages proficiently is not just about solving mathematical problems; it’s about developing a crucial life skill that allows you to make informed decisions in various contexts – from managing your finances to analyzing data effectively.
Frequently Asked Questions (FAQ)
-
Q: How can I calculate a percentage without a calculator?
- A: For simpler percentages, you can use the fractional method or mental math techniques. For more complex calculations, pen and paper can be effectively used by breaking down the multiplication into smaller, manageable steps.
-
Q: What if the percentage is greater than 100%?
- A: A percentage greater than 100% signifies a value exceeding the original number. For example, 120% of 35 would be 35 * 1.2 = 42. This is commonly used in contexts like growth or increase.
-
Q: How can I calculate the percentage one number represents of another?
- A: To find what percentage one number represents of another, divide the first number by the second number and then multiply by 100. For instance, to find what percentage 20 is of 50, you would calculate (20/50) * 100 = 40%.
-
Q: Are there any online tools or calculators to help with percentage calculations?
- A: Yes, many online calculators are readily available to assist with percentage calculations. These calculators can be particularly useful for more complex calculations or when checking your work.
Conclusion
Calculating 90% of 35, while seemingly a simple problem, serves as a gateway to understanding the broader world of percentage calculations and their widespread applications. Mastering this fundamental concept equips you with a valuable skill applicable to various aspects of life, from personal finance to professional analysis. Remember the key steps: convert the percentage to a decimal and multiply by the given number. By understanding the underlying principles and practicing regularly, you can confidently tackle any percentage-related problem you encounter. Embrace the power of percentages and unlock a world of mathematical understanding!
Latest Posts
Latest Posts
-
32 Of 300
Sep 22, 2025
-
43kg In Stones
Sep 22, 2025
-
112 2kg In Stone
Sep 22, 2025
-
1 86 In Ft
Sep 22, 2025
-
Hunger Games Clove
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 90 Of 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.