9 X 20
interactiveleap
Sep 25, 2025 · 7 min read
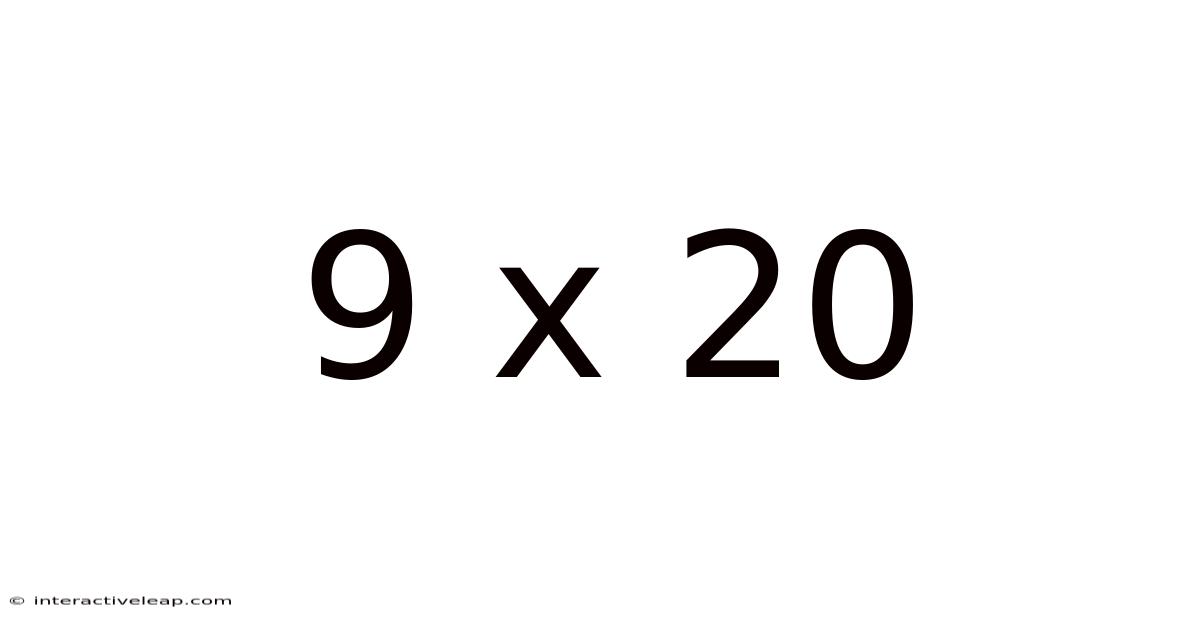
Table of Contents
Unveiling the Mysteries of 9 x 20: A Deep Dive into Multiplication
This article explores the seemingly simple multiplication problem of 9 x 20, delving far beyond the immediate answer to reveal the underlying mathematical concepts, practical applications, and even its connection to broader mathematical principles. We'll explore different methods of solving this problem, examining their relative strengths and weaknesses, and ultimately demonstrating how a seemingly basic calculation can illuminate fundamental mathematical ideas. This exploration is designed for anyone, from elementary school students grasping multiplication fundamentals to adults seeking a refresher or deeper understanding of mathematical thinking.
Understanding the Fundamentals: What is 9 x 20?
At its core, 9 x 20 represents repeated addition. It asks: what is the sum of nine 20s? Or, equivalently, what is the total value of twenty groups of nine items each? The most straightforward approach is to perform repeated addition: 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 + 20 = 180. This method, while effective for smaller numbers, becomes cumbersome as numbers grow larger.
Efficient Calculation Methods: Beyond Repeated Addition
Fortunately, mathematics provides more efficient techniques. The commutative property of multiplication allows us to switch the order of the numbers without changing the result (9 x 20 = 20 x 9). This seemingly small detail opens up opportunities for simplification. We can break down 20 into smaller, more manageable components:
-
Using the distributive property: We can rewrite 20 as (10 + 10). Applying the distributive property, we get: 9 x (10 + 10) = (9 x 10) + (9 x 10) = 90 + 90 = 180. This method leverages the ease of multiplying by 10, a common shortcut in arithmetic.
-
Using multiplication by 10: We can recognize that 20 is simply 2 x 10. Therefore, 9 x 20 can be expressed as 9 x (2 x 10). Using the associative property of multiplication (which allows us to regroup numbers), we get (9 x 2) x 10 = 18 x 10 = 180. This elegantly demonstrates the power of breaking down complex problems into simpler ones.
-
Visual Representation: Imagine a rectangular array with 9 rows and 20 columns. Counting the total number of squares within this array gives you the product. This visual approach is particularly helpful for beginners to grasp the concept of multiplication.
Exploring the Number 180: Factors and Multiples
The result of 9 x 20, which is 180, offers further avenues for exploration. Let's analyze its factors and multiples:
-
Factors: The factors of 180 are the numbers that divide 180 evenly. These include 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180. Understanding factors helps in simplifying fractions and solving various mathematical problems.
-
Multiples: The multiples of 180 are numbers obtained by multiplying 180 by any whole number. For example, some multiples of 180 are 180, 360, 540, 720, and so on. This concept is crucial in understanding number patterns and sequences.
-
Prime Factorization: Breaking down 180 into its prime factors (numbers divisible only by 1 and themselves) reveals a deeper structure. The prime factorization of 180 is 2² x 3² x 5. This representation is unique to each number and is fundamental in various areas of mathematics, including number theory and cryptography.
Real-World Applications: Where do we see 9 x 20?
While the multiplication problem of 9 x 20 might seem abstract, it finds practical applications in numerous everyday scenarios:
-
Calculating Costs: Imagine buying 9 items priced at $20 each. The total cost is easily calculated as 9 x 20 = $180.
-
Measuring Areas: A rectangular garden measuring 9 meters by 20 meters has an area of 180 square meters.
-
Unit Conversions: Converting units often involves multiplication. For example, if a recipe calls for 20 milliliters of liquid per serving and you need 9 servings, you would need 180 milliliters of liquid in total.
-
Data Analysis: In data analysis, you may encounter scenarios where you need to calculate the total number of items based on groupings. If you have 9 groups with 20 items in each, you have a total of 180 items.
These examples show that understanding this seemingly basic multiplication problem is directly relevant to various real-world calculations and problem-solving situations.
Connecting 9 x 20 to Broader Mathematical Concepts
The seemingly simple calculation of 9 x 20 is intrinsically linked to several important mathematical concepts:
-
The Commutative Property: As previously mentioned, the commutative property of multiplication allows us to switch the order of the operands without changing the product (a x b = b x a). This property simplifies calculations and provides flexibility in problem-solving.
-
The Distributive Property: The distributive property allows us to multiply a number by a sum (a x (b + c) = (a x b) + (a x c)). This property is fundamental in algebraic manipulation and simplification.
-
The Associative Property: The associative property allows us to regroup numbers in a multiplication problem without affecting the outcome ((a x b) x c = a x (b x c)). This property is essential in simplifying complex expressions.
-
Number Theory: The analysis of the factors, multiples, and prime factorization of 180 is central to number theory, a branch of mathematics that explores the properties of integers.
-
Algebra: Understanding the principles behind 9 x 20 lays a strong foundation for algebraic concepts such as variables and equations.
By exploring 9 x 20, we touch upon fundamental algebraic and number theory principles that are crucial for further mathematical development.
Beyond the Basics: Extending the Understanding
The understanding of 9 x 20 can be extended to more complex mathematical concepts. For instance:
-
Working with larger numbers: Applying the same principles, we can efficiently solve more complex multiplication problems involving larger numbers. Understanding the underlying logic enables us to tackle more challenging calculations with greater confidence.
-
Exploring different bases: While we work primarily in base-10 (decimal system), the concept of multiplication transcends the base. We can explore multiplication in binary, hexadecimal, or other number systems using the same fundamental principles.
-
Developing problem-solving skills: The ability to break down a problem into smaller, manageable parts, as demonstrated with the different methods of calculating 9 x 20, is a valuable problem-solving skill applicable across various disciplines.
Frequently Asked Questions (FAQ)
Q: What is the quickest way to calculate 9 x 20?
A: The quickest way is to recognize that 20 is twice 10. Therefore, calculate 9 x 10 = 90, then double the result (90 x 2 = 180).
Q: How can I explain 9 x 20 to a young child?
A: Use visual aids like blocks or drawings. Arrange 9 groups of 20 blocks each. Counting all the blocks will demonstrate the answer of 180.
Q: What are some real-world examples of using 9 x 20?
A: Calculating the total cost of 9 items priced at $20 each, determining the area of a 9m x 20m rectangle, or converting units in a recipe.
Q: Is there a way to solve 9 x 20 without using multiplication tables?
A: Yes, using repeated addition (20 + 20 + ... + 20, nine times), the distributive property, or breaking down 20 into smaller factors (e.g., 2 x 10).
Q: Why is understanding 9 x 20 important?
A: It reinforces fundamental mathematical concepts like the commutative, associative, and distributive properties. It also demonstrates practical applications of multiplication in everyday situations. It builds a foundation for more advanced mathematical concepts.
Conclusion: The Significance of a Simple Calculation
The seemingly simple calculation of 9 x 20 offers a rich and multifaceted exploration into the world of mathematics. It serves not only as a basic arithmetic problem but also as a gateway to understanding fundamental mathematical principles, practical applications, and the interconnectedness of various mathematical concepts. By unraveling the mysteries behind this single calculation, we enhance our understanding of numbers, operations, and the power of mathematical thinking – a skill applicable far beyond the realm of numbers themselves. The journey from a basic multiplication problem to a deeper appreciation of mathematical principles highlights the elegance and power of mathematics, encouraging a lifelong exploration of this fascinating field.
Latest Posts
Latest Posts
-
Creative In French
Sep 25, 2025
-
10 Of 145
Sep 25, 2025
-
Weeds Are Flowers
Sep 25, 2025
-
20mph In Km
Sep 25, 2025
-
5x 12 0
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 9 X 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.