9/2 As Decimal
interactiveleap
Sep 14, 2025 · 5 min read
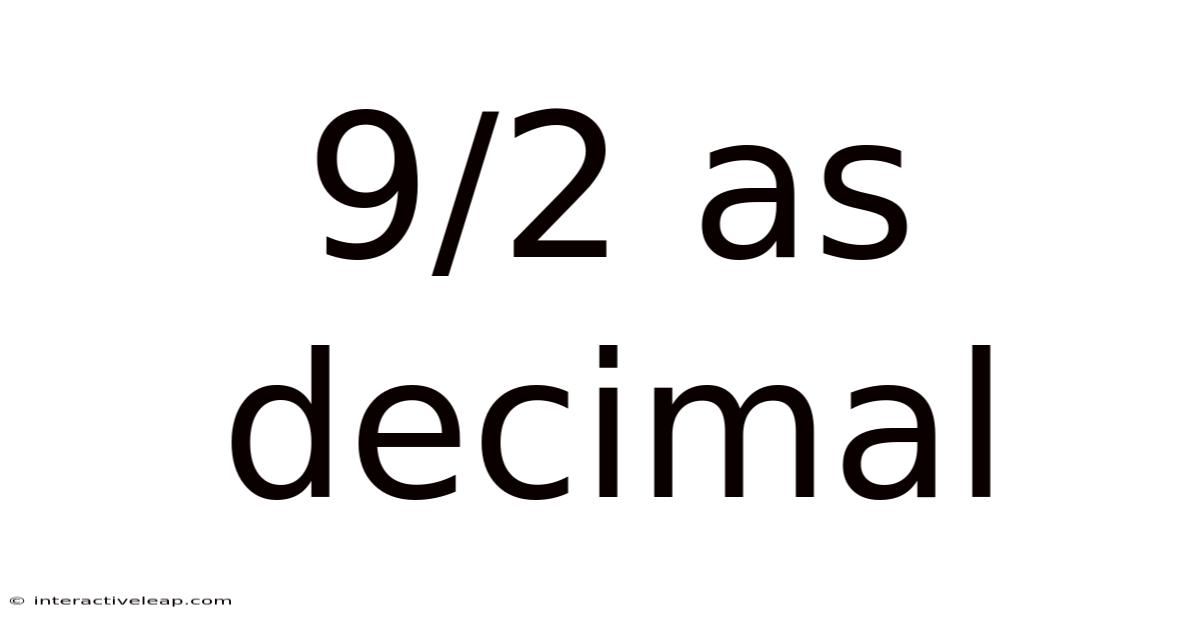
Table of Contents
Unveiling the Mystery: 9/2 as a Decimal and Beyond
The seemingly simple fraction 9/2 often presents a minor hurdle for those unfamiliar with fraction-to-decimal conversions. This comprehensive guide will not only show you how to convert 9/2 into its decimal equivalent but also delve into the underlying principles, explore related concepts, and answer frequently asked questions. Understanding this conversion is fundamental to grasping more complex mathematical concepts. By the end of this article, you'll be able to confidently tackle similar conversions and appreciate the elegance of mathematical transformations.
Understanding Fractions and Decimals
Before jumping into the conversion of 9/2, let's establish a solid foundation. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
A decimal, on the other hand, is a way of expressing a number using base-10. The decimal point separates the whole number part from the fractional part. Each digit to the right of the decimal point represents a decreasing power of 10 (tenths, hundredths, thousandths, and so on).
The key to converting a fraction to a decimal is recognizing that the fraction represents a division problem. The numerator is divided by the denominator.
Converting 9/2 to a Decimal: The Simple Approach
The most straightforward way to convert 9/2 to a decimal is to perform the division:
9 ÷ 2 = 4.5
Therefore, 9/2 as a decimal is 4.5. This is a terminating decimal, meaning the decimal representation ends after a finite number of digits.
A Deeper Dive: Understanding the Division Process
Let's break down the division process to further solidify understanding. When we divide 9 by 2, we ask: "How many times does 2 go into 9?"
- 2 goes into 9 four times (2 x 4 = 8).
- This leaves a remainder of 1 (9 - 8 = 1).
- Since we're working with decimals, we add a decimal point to the dividend (9) and a zero to the remainder (1), making it 10.
- 2 goes into 10 five times (2 x 5 = 10).
- The remainder is 0, indicating the division is complete.
Thus, the quotient (result of the division) is 4.5.
Visualizing the Fraction: A Geometric Approach
Imagine a rectangular cake divided into two equal pieces. The fraction 9/2 represents nine such halves. We can group these halves into whole cakes and remaining parts.
- Four pairs of halves make four whole cakes (4 x 2 = 8 halves).
- This leaves one half remaining.
- Therefore, we have four whole cakes and one-half of a cake, which corresponds to the decimal 4.5.
Exploring Related Concepts: Improper Fractions and Mixed Numbers
The fraction 9/2 is an improper fraction, meaning the numerator (9) is greater than or equal to the denominator (2). Improper fractions can be converted into mixed numbers, which consist of a whole number and a proper fraction.
To convert 9/2 to a mixed number:
- Divide the numerator (9) by the denominator (2): 9 ÷ 2 = 4 with a remainder of 1.
- The whole number part of the mixed number is the quotient (4).
- The fractional part of the mixed number is the remainder (1) over the original denominator (2), which is 1/2.
Therefore, 9/2 as a mixed number is 4 1/2. This visually represents four whole units and an additional half.
Decimal Representation and Place Value
The decimal 4.5 can be further broken down using place value:
- 4: Represents four units (ones).
- 5: Represents five tenths (0.5).
This understanding of place value is crucial for comprehending decimal operations and conversions.
Converting Other Fractions to Decimals: A Practical Guide
The method used to convert 9/2 to a decimal can be applied to other fractions. Remember the crucial step: divide the numerator by the denominator. Sometimes, the resulting decimal will be terminating (like 4.5), while others will be repeating decimals (e.g., 1/3 = 0.333...). Repeating decimals are denoted by placing a bar over the repeating digit(s).
Frequently Asked Questions (FAQs)
Q1: What if the fraction has a larger denominator? Will the process be different?
A1: No, the process remains the same. You simply divide the numerator by the denominator. The decimal representation might have more digits, and it might be a repeating decimal.
Q2: Can I use a calculator to convert fractions to decimals?
A2: Yes, calculators are a convenient tool for performing this conversion. Simply enter the numerator, then the division symbol, then the denominator.
Q3: Are there different methods for converting fractions to decimals?
A3: While long division is the most fundamental method, other techniques might be used depending on the specific fraction and desired level of precision. For example, you might recognize common fraction-decimal equivalents (like 1/4 = 0.25).
Q4: What is the significance of understanding fraction-to-decimal conversions?
A4: This fundamental skill underpins many mathematical concepts, including percentages, ratios, proportions, and various applications in science, engineering, and everyday life. Proficiency in these conversions enhances your overall numerical literacy.
Q5: How do I handle negative fractions?
A5: Simply perform the division as you normally would, and then apply the negative sign to the result. For example, -9/2 = -4.5.
Conclusion: Mastering Fractions and Decimals
Converting 9/2 to its decimal equivalent, 4.5, is a simple yet powerful illustration of a fundamental mathematical concept. Understanding the process, its underlying principles, and related concepts like mixed numbers and repeating decimals is crucial for mathematical fluency. This knowledge extends far beyond simple conversions, forming the bedrock for more advanced mathematical studies and real-world applications. By practicing these concepts and exploring further examples, you'll confidently navigate the world of fractions and decimals, solidifying your mathematical foundation.
Latest Posts
Latest Posts
-
99kg To Stone
Sep 14, 2025
-
Sparx Maths Answers
Sep 14, 2025
-
Pink To Yellow
Sep 14, 2025
-
Disadvantages Of Ssd
Sep 14, 2025
-
49 4kg In Stone
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 9/2 As Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.