80 Of 36
interactiveleap
Sep 22, 2025 · 6 min read
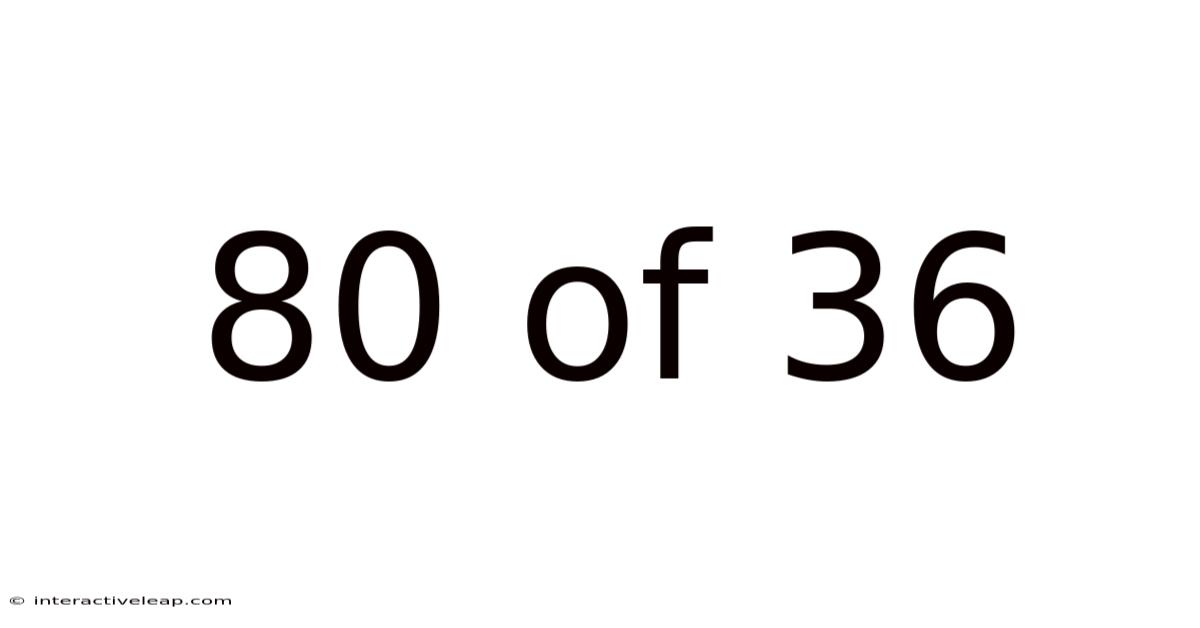
Table of Contents
Deconstructing 80/36: Understanding the Ratio and its Applications
The ratio 80/36, while seemingly simple at first glance, opens doors to a fascinating exploration of mathematical concepts, real-world applications, and problem-solving strategies. This article delves deep into the meaning of this ratio, exploring its simplification, practical uses across various fields, and the broader mathematical principles it represents. We'll uncover why understanding ratios is crucial and how this specific ratio, 80/36, can be a valuable tool in your mathematical toolkit.
Understanding Ratios: A Foundation
Before we dive into the specifics of 80/36, let's solidify our understanding of ratios. A ratio is a comparison of two or more quantities. It expresses the relative size of one quantity to another. Ratios can be written in several ways:
- Using a colon: 80:36
- As a fraction: 80/36
- In words: 80 to 36
Understanding ratios is essential in various fields, from cooking and construction to finance and science. They help us understand proportions, scale, and relationships between different quantities.
Simplifying 80/36: Finding the Greatest Common Divisor (GCD)
The ratio 80/36 can be simplified to its lowest terms by finding the greatest common divisor (GCD) of 80 and 36. The GCD is the largest number that divides both 80 and 36 without leaving a remainder. We can find the GCD using several methods:
-
Prime Factorization: We find the prime factors of both numbers.
- 80 = 2 x 2 x 2 x 2 x 5 = 2⁴ x 5
- 36 = 2 x 2 x 3 x 3 = 2² x 3² The common factors are 2² = 4. Therefore, the GCD is 4.
-
Euclidean Algorithm: This iterative method involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
- 80 ÷ 36 = 2 with a remainder of 8
- 36 ÷ 8 = 4 with a remainder of 4
- 8 ÷ 4 = 2 with a remainder of 0 The GCD is 4.
Now that we have the GCD (4), we can simplify the ratio:
80/36 = (80 ÷ 4) / (36 ÷ 4) = 20/9
Therefore, the simplified form of the ratio 80/36 is 20:9 or 20/9. This simplified form retains the same proportional relationship as the original ratio, making it easier to work with and understand.
Real-World Applications of Ratios: Beyond the Classroom
The applications of ratios extend far beyond theoretical mathematics. Let's explore some examples:
-
Scaling and proportions: Imagine you're enlarging a photograph. If the original photo has a ratio of width to height as 80:36 (or 20:9), maintaining this ratio during enlargement ensures the picture remains proportionally correct, avoiding distortion. This principle applies to various design and engineering projects.
-
Mixing ingredients: Recipes often use ratios to specify ingredient quantities. For instance, a recipe might call for a ratio of 80 grams of flour to 36 grams of sugar. Understanding and simplifying this ratio (20:9) allows for scaling the recipe up or down while maintaining the correct proportions of ingredients.
-
Financial analysis: Ratios are crucial in financial analysis for assessing a company's performance. For example, the debt-to-equity ratio compares a company's debt to its equity, providing insights into its financial risk. While 80/36 wouldn't directly represent a specific financial ratio, the principle of comparing two quantities remains the same. Understanding how to work with ratios is foundational to interpreting these financial indicators.
-
Probability and statistics: Ratios are fundamental in calculating probabilities. If there are 80 red balls and 36 blue balls in a bag, the ratio 80/36 represents the probability of selecting a red ball relative to a blue ball. Simplifying this ratio (20/9) helps in understanding and comparing these probabilities.
-
Map scales: Maps use ratios to represent distances. A map scale might be represented as 1:100,000, meaning one unit on the map equals 100,000 units in reality. The concept of scaling using ratios is central to map-making and interpretation.
-
Engineering and construction: In engineering and construction, ratios are used to determine the proportions of materials in concrete mixes, the dimensions of structural elements, and the strengths of various materials. Understanding ratios is crucial for ensuring safety and structural integrity in construction projects.
Beyond 80/36: Exploring Related Mathematical Concepts
Understanding the ratio 80/36 opens doors to exploring several related mathematical concepts:
-
Proportions: A proportion is a statement that two ratios are equal. We can express the ratio 80/36 as a proportion: 80/36 = 20/9. Understanding proportions allows us to solve for unknown quantities in related ratios. For example, if we know one part of a proportion, we can use cross-multiplication to find the unknown value.
-
Percentages: Ratios can be easily converted into percentages. To convert 80/36 into a percentage, we divide 80 by 36 and multiply by 100: (80/36) * 100 ≈ 222.22%. This provides another way to represent and compare the relative sizes of the quantities.
-
Fractions and decimals: Ratios are essentially fractions. The ratio 80/36 is a fraction that can be converted to a decimal by performing the division: 80 ÷ 36 ≈ 2.22. Understanding the interrelationship between ratios, fractions, and decimals is crucial for mathematical fluency.
Frequently Asked Questions (FAQ)
-
Q: What are some common mistakes people make when working with ratios?
- A: A common mistake is incorrectly simplifying ratios. It's crucial to find the greatest common divisor to achieve the simplest form. Another mistake is not understanding the order of the quantities in the ratio. The order matters as 80/36 is different from 36/80.
-
Q: How can I practice working with ratios?
- A: Practice with various real-world examples. Try simplifying ratios encountered in cooking recipes, map scales, or financial data. Solve problems involving proportions. Online resources and textbooks provide plenty of exercises to hone your skills.
-
Q: Are there any limitations to using ratios?
- A: Ratios are effective for comparing quantities of the same units. Comparing quantities with different units (e.g., kilograms and meters) requires careful consideration and often involves additional conversions.
-
Q: What is the significance of simplifying ratios?
- A: Simplifying ratios makes them easier to understand and work with. It helps in comparing ratios more effectively and reduces the risk of calculation errors. The simplified ratio retains the same proportional relationship as the original, making it a more efficient representation.
Conclusion: The Power of Understanding 80/36 and Beyond
The seemingly simple ratio 80/36 offers a gateway to a deeper understanding of mathematical concepts and their widespread applications. By exploring its simplification, real-world applications, and related mathematical principles, we've uncovered its significance. The ability to understand, simplify, and apply ratios is a valuable skill in various fields, from everyday tasks to complex problem-solving in science, engineering, and finance. Mastering this fundamental concept equips you with a powerful tool for understanding the world around us and tackling numerous mathematical challenges. Remember, the journey of learning is continuous, and every step, like understanding a ratio like 80/36, contributes to a richer mathematical understanding and problem-solving ability.
Latest Posts
Latest Posts
-
220mm In Inches
Sep 22, 2025
-
Car Average Length
Sep 22, 2025
-
122 Pounds Kg
Sep 22, 2025
-
102cm In Feet
Sep 22, 2025
-
280ml In Oz
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 80 Of 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.