80 Of 160
interactiveleap
Sep 18, 2025 · 5 min read
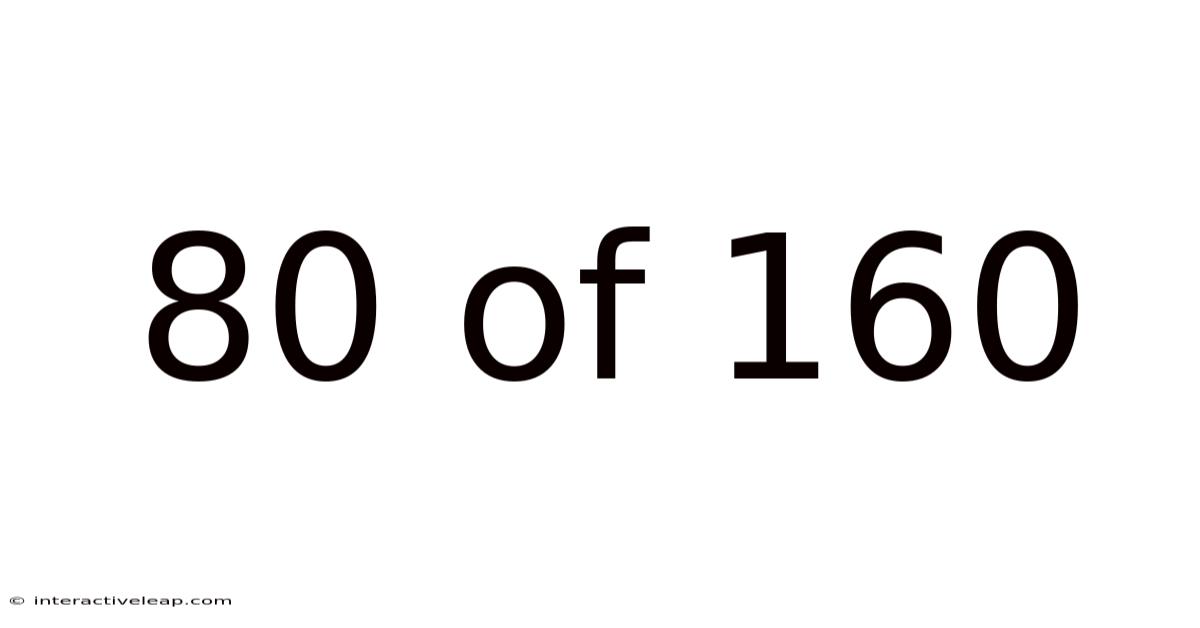
Table of Contents
Understanding 80 out of 160: Fractions, Percentages, and Real-World Applications
Understanding the relationship between 80 and 160, represented as "80 out of 160," is a fundamental concept in mathematics with wide-ranging applications in everyday life. This seemingly simple fraction holds the key to understanding percentages, ratios, and proportions – crucial skills for everything from calculating grades to comprehending complex data analysis. This article will delve into various methods of interpreting and calculating "80 out of 160," exploring its significance and practical applications.
Introduction: Deconstructing the Fraction 80/160
The phrase "80 out of 160" represents a fraction: 80/160. This fraction indicates that we have 80 parts out of a total of 160 parts. To fully understand this relationship, we need to explore several key mathematical concepts.
1. Simplifying the Fraction
The first step in understanding 80/160 is to simplify it to its lowest terms. We can do this by finding the greatest common divisor (GCD) of both the numerator (80) and the denominator (160). The GCD of 80 and 160 is 80. Dividing both the numerator and the denominator by 80, we get:
80 ÷ 80 / 160 ÷ 80 = 1/2
This simplified fraction, 1/2, represents the same proportion as 80/160. This simplification makes the fraction easier to understand and work with in further calculations.
2. Converting to a Percentage
Fractions are often expressed as percentages to provide a more intuitive understanding of the proportion. To convert 1/2 (or 80/160) to a percentage, we multiply the fraction by 100%:
(1/2) * 100% = 50%
Therefore, 80 out of 160 represents 50%. This means that 80 is 50% of 160. This percentage representation is crucial for comparing proportions and visualizing the data effectively.
3. Understanding Ratios and Proportions
The relationship between 80 and 160 can also be expressed as a ratio. A ratio compares two quantities. In this case, the ratio is 80:160, which simplifies to 1:2. This ratio indicates that for every one part, there are two parts in total.
Proportions are statements of equality between two ratios. For example, if we have a proportion of 80/160 = x/200, we can solve for 'x' to find an equivalent proportion:
80/160 = x/200 Cross-multiplying: 80 * 200 = 160 * x 16000 = 160x x = 100
This shows that 100 out of 200 is equivalent to 80 out of 160, both representing 50%.
4. Real-World Applications: Illustrative Examples
The concept of "80 out of 160" (or 50%) appears frequently in various real-world scenarios:
- Academic Performance: If a student answers 80 questions correctly out of a total of 160 questions on an exam, their score is 50%.
- Sales and Marketing: If a company sets a sales target of 160 units and achieves 80 units, they have achieved 50% of their target.
- Financial Investments: If an investment of $160 yields a return of $80, the return on investment (ROI) is 50%.
- Survey Results: If 80 out of 160 respondents to a survey agree with a particular statement, the agreement rate is 50%.
- Sports Statistics: If a basketball player attempts 160 shots and makes 80, their shooting percentage is 50%.
- Project Management: If a project has 160 tasks and 80 tasks are completed, the project is 50% complete.
These examples highlight the versatility of understanding fractions, percentages, and ratios. The ability to interpret and calculate these values is essential for making informed decisions and effectively analyzing data in various fields.
5. Further Exploration: Beyond the Basics
While understanding the fundamental calculations related to 80/160 is crucial, further exploration can enhance comprehension:
- Decimal Representation: The fraction 1/2 can also be expressed as a decimal: 0.5. This representation is often used in calculations involving computers or other electronic devices.
- Working with Larger Numbers: The same principles apply to larger numbers. For example, understanding 800 out of 1600 is still 50%, showing the scalability of these concepts.
- Visual Representation: Using charts and graphs to visualize the proportion 80/160 (or 50%) can aid in understanding and communication. A pie chart showing a 50/50 split is a powerful visual representation.
- Comparative Analysis: Understanding 80/160 allows for the comparison of different proportions. For instance, we can compare this to other ratios like 60/160 (37.5%) or 120/160 (75%). This comparative analysis is key to making informed decisions based on data.
6. Frequently Asked Questions (FAQs)
Q1: How do I calculate the percentage if the numbers aren't easily divisible?
A1: If the numbers aren't easily divisible, you can use a calculator or perform long division. Divide the numerator by the denominator and multiply the result by 100%. For example, to find the percentage for 75 out of 150: 75/150 = 0.5 * 100% = 50%.
Q2: What if I have more than two numbers involved in the proportion?
A2: If you have more complex proportions involving multiple quantities, you'll need to consider ratios and proportions more comprehensively. Solving these problems often involves setting up equations and solving for the unknown variable(s).
Q3: Why is it important to simplify fractions?
A3: Simplifying fractions makes them easier to understand and work with. A simplified fraction represents the same proportion in a more concise and manageable form. It reduces the complexity of calculations and allows for easier comparisons.
Q4: Can I use different methods to solve proportions?
A4: Yes, there are different methods for solving proportions, including cross-multiplication, scaling, and using unit rates. Choosing the most appropriate method depends on the specific problem and the context.
Q5: How can I improve my understanding of fractions, percentages, and ratios?
A5: Practice is key! Work through various examples, solve different types of problems, and utilize online resources and tutorials to reinforce your understanding.
7. Conclusion: The Significance of Understanding Proportions
The seemingly simple concept of "80 out of 160" encompasses a wealth of mathematical principles. By mastering the ability to simplify fractions, convert to percentages, understand ratios and proportions, and apply these concepts to real-world scenarios, individuals equip themselves with valuable problem-solving skills applicable to various aspects of life. From academic success to professional endeavors, the understanding of proportions remains a cornerstone of numeracy and effective data interpretation. Consistent practice and application of these principles are key to developing a strong mathematical foundation and enhancing analytical capabilities. The ability to confidently interpret and utilize these concepts contributes significantly to informed decision-making and a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
93 Miles Km
Sep 18, 2025
-
6 Times 3
Sep 18, 2025
-
56kh In Stone
Sep 18, 2025
-
53kg To Stone
Sep 18, 2025
-
3 X 60
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 80 Of 160 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.