80 Of 14
interactiveleap
Sep 24, 2025 · 5 min read
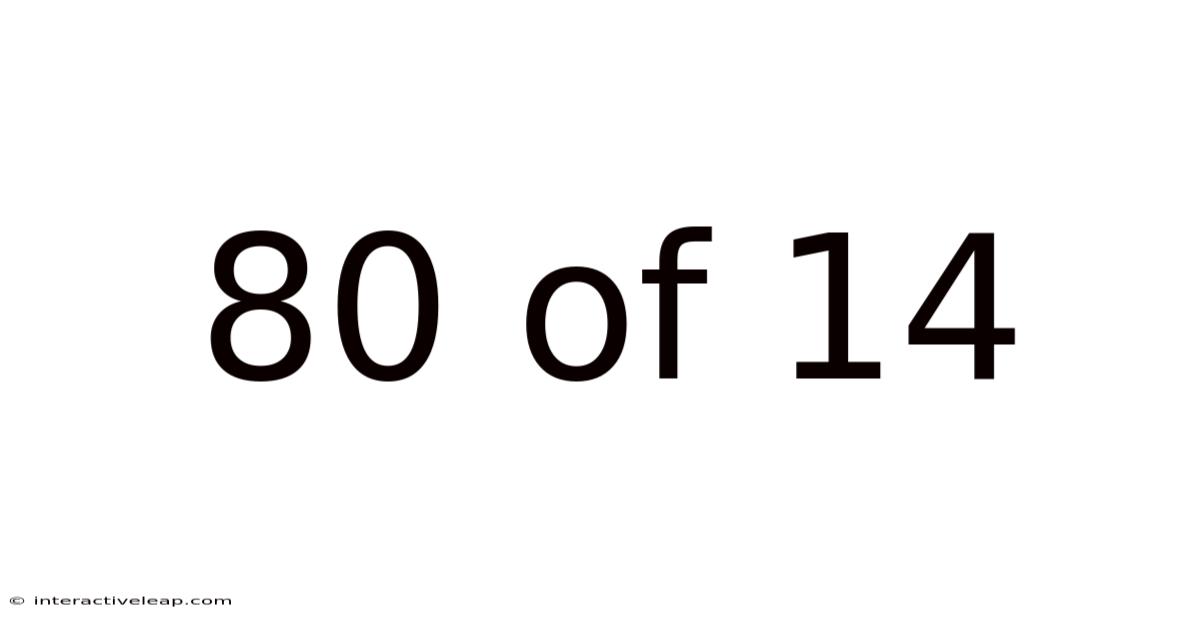
Table of Contents
Decoding the Fraction 80/14: A Deep Dive into Simplification, Decimals, and Real-World Applications
Understanding fractions is a cornerstone of mathematical literacy. This article will explore the fraction 80/14 in detail, covering its simplification, decimal representation, practical applications, and addressing common misconceptions. We'll move beyond simple calculation to delve into the underlying principles and contextual understanding of this seemingly straightforward fraction. Learning to work with fractions like 80/14 is crucial for various fields, from cooking and construction to advanced mathematics and computer programming.
Understanding the Fraction 80/14
The fraction 80/14 represents 80 parts out of a total of 14 parts. This is an improper fraction because the numerator (80) is larger than the denominator (14). Improper fractions are often easier to work with in calculations than their mixed number equivalents.
1. Simplifying the Fraction
Before we proceed, it’s essential to simplify the fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator and the denominator. The GCD is the largest number that divides both 80 and 14 without leaving a remainder.
To find the GCD, we can use the Euclidean algorithm.
- Step 1: Divide the larger number (80) by the smaller number (14): 80 ÷ 14 = 5 with a remainder of 10.
- Step 2: Replace the larger number with the remainder (10) and repeat: 14 ÷ 10 = 1 with a remainder of 4.
- Step 3: Repeat: 10 ÷ 4 = 2 with a remainder of 2.
- Step 4: Repeat: 4 ÷ 2 = 2 with a remainder of 0.
The last non-zero remainder is the GCD, which is 2.
Now, we divide both the numerator and the denominator by the GCD:
80 ÷ 2 = 40 14 ÷ 2 = 7
Therefore, the simplified form of 80/14 is 40/7.
2. Converting to a Mixed Number
An improper fraction can be converted into a mixed number, which combines a whole number and a proper fraction. To do this, we divide the numerator (40) by the denominator (7):
40 ÷ 7 = 5 with a remainder of 5.
This means that 40/7 can be expressed as 5 5/7. This indicates 5 whole units and 5/7 of another unit.
3. Converting to a Decimal
To express 40/7 as a decimal, we perform the division:
40 ÷ 7 ≈ 5.7142857...
This is a repeating decimal, indicated by the ellipsis (...). The digits "714285" repeat infinitely. For practical purposes, we might round the decimal to a specific number of decimal places, depending on the required accuracy. For example, rounded to two decimal places, it is 5.71.
Real-World Applications of Fractions like 80/14
Fractions are indispensable tools in numerous real-life situations. Let's explore a few examples where understanding fractions, particularly improper fractions like 80/14, is crucial:
-
Cooking and Baking: Recipes often require precise measurements. If a recipe calls for 80 grams of flour and you only have a scale that measures in multiples of 14 grams, you’d need to calculate 80/14 to determine how many measurements you need.
-
Construction and Engineering: In construction, accurate measurements are critical. Imagine calculating the amount of material needed for a project where you have a total length of 80 units and each unit requires 14 pieces of a specific material.
-
Finance and Budgeting: Fractions are fundamental in financial calculations. For instance, if you need to distribute $80 among 14 people equally, you would need to calculate 80/14 to determine each person's share.
-
Data Analysis and Statistics: Fractions are essential for representing proportions and percentages in data analysis and statistical studies. For instance, if 80 out of 140 survey respondents answered "yes" to a particular question, the fraction 80/140 (which simplifies to 4/7) represents the proportion of "yes" responses.
-
Computer Science and Programming: Fractions and their decimal representations are extensively used in computer programming for calculations, image processing, and representing data structures.
Addressing Common Misconceptions
Several common misconceptions surround fractions, especially improper fractions. Let's address some of them:
-
Improper fractions are "wrong": Improper fractions are not inherently incorrect; they are simply another way of representing a quantity. They are often more useful in calculations than mixed numbers.
-
Simplifying fractions is optional: While you can perform calculations with unsimplified fractions, simplifying them makes calculations easier and reduces the chance of errors. Moreover, the simplified fraction represents the same value more concisely.
-
Decimals are always more accurate: While decimals are convenient for many applications, they can sometimes lead to rounding errors, especially when dealing with repeating decimals. Fractions offer exact representation in many cases.
Further Exploration
Beyond the basic understanding of simplification, conversion, and application, the fraction 80/14 opens doors to more advanced mathematical concepts:
-
Continued Fractions: The fraction 40/7 can be expressed as a continued fraction, offering another way to represent its value.
-
Rational Numbers: Fractions represent rational numbers, which are numbers that can be expressed as a ratio of two integers. Understanding rational numbers is essential for grasping more advanced mathematical concepts.
-
Approximations: The decimal representation of 40/7 provides an approximation. Exploring error analysis helps understand the difference between the exact value and its approximation.
-
Proportions and Ratios: The fraction 80/14 can be used to solve problems involving proportions and ratios. Understanding these concepts is crucial for many real-world applications.
Conclusion
The fraction 80/14, seemingly simple at first glance, provides a rich foundation for exploring fundamental mathematical concepts. By understanding its simplification, decimal representation, and diverse applications, we gain a deeper appreciation for the power and versatility of fractions. This exploration extends beyond rote memorization to a contextual understanding of how fractions represent real-world quantities and form the basis for more advanced mathematical concepts. Mastering fractions like 80/14 is a valuable step towards achieving greater mathematical proficiency and applying that knowledge across various disciplines. The key takeaway is not simply the numerical answer, but the process of understanding, simplifying, and applying this knowledge to solve problems creatively and accurately.
Latest Posts
Latest Posts
-
1 85m In Ft
Sep 24, 2025
-
Zeta 1 Reticuli
Sep 24, 2025
-
20 Of 155
Sep 24, 2025
-
175kg In Pounds
Sep 24, 2025
-
6 Foot Tall
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 80 Of 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.