8 Of 200
interactiveleap
Sep 20, 2025 · 6 min read
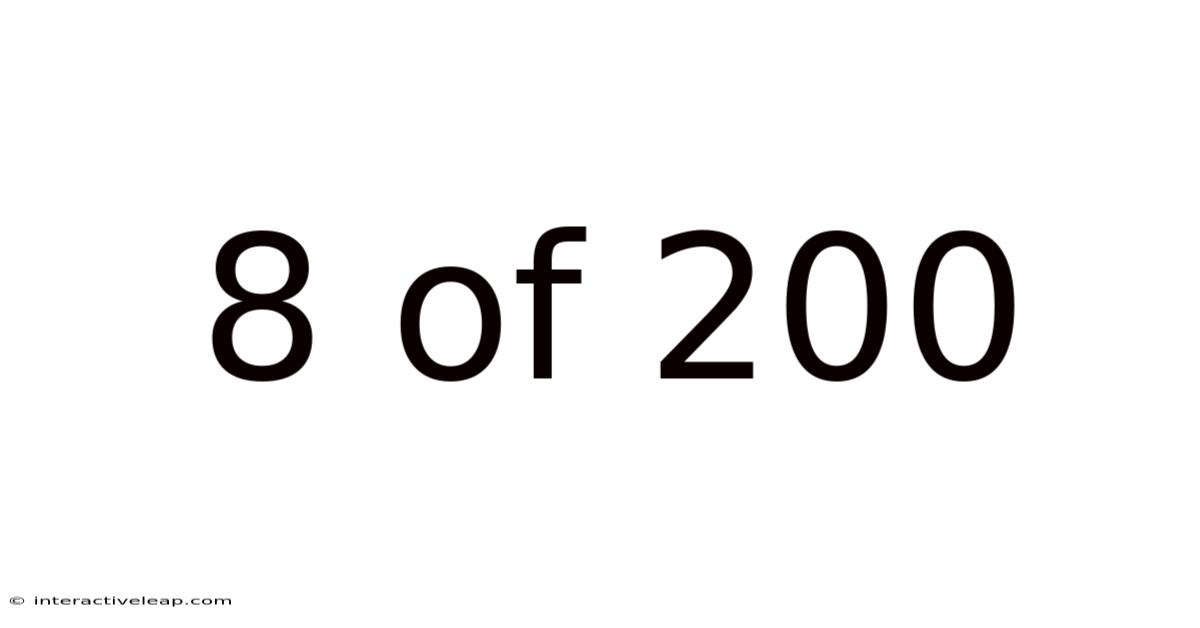
Table of Contents
Decoding the Enigma: Understanding the Fraction 8/200 and its Implications
The seemingly simple fraction 8/200 might appear insignificant at first glance. However, understanding its implications extends far beyond basic arithmetic. This seemingly small fraction can serve as a gateway to understanding core concepts in mathematics, statistics, and even real-world applications. This article will delve deep into the fraction 8/200, exploring its simplification, decimal representation, percentage equivalent, and practical applications, ultimately aiming to illuminate its significance and demonstrate its relevance in various contexts.
I. Simplifying 8/200: The Power of Reduction
The first step in understanding 8/200 is to simplify it to its lowest terms. This process involves finding the greatest common divisor (GCD) of the numerator (8) and the denominator (200). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
In this case, the GCD of 8 and 200 is 8. Dividing both the numerator and denominator by 8, we get:
8 ÷ 8 = 1 200 ÷ 8 = 25
Therefore, the simplified form of 8/200 is 1/25. This simplified fraction is much easier to work with and provides a clearer understanding of the fraction's true value. This process of simplification is crucial in mathematics as it allows for easier calculations and comparisons.
II. Decimal Representation: From Fraction to Decimal
Converting a fraction to a decimal is a fundamental mathematical skill. To convert 1/25 (the simplified form of 8/200) to a decimal, we perform a simple division:
1 ÷ 25 = 0.04
Thus, the decimal representation of 8/200 is 0.04. This decimal form is useful for calculations involving other decimal numbers and is often preferred in certain applications, especially those involving technology and data analysis. Understanding both fractional and decimal representations is crucial for mathematical fluency.
III. Percentage Equivalent: Expressing the Fraction as a Percentage
Percentages are commonly used to express proportions and ratios. To convert the fraction 1/25 (or 0.04) to a percentage, we multiply it by 100:
0.04 × 100 = 4%
Therefore, 8/200 is equivalent to 4%. This percentage representation offers a readily understandable way to communicate the relative size of the fraction, making it easily relatable in various contexts, such as expressing a portion of a whole, calculating discounts, or representing statistical data.
IV. Practical Applications: Where does 8/200 (or 4%) show up?
While seemingly small, the fraction 8/200, or its equivalent 4%, appears in a surprising number of real-world scenarios:
-
Statistics and Probability: In statistical analysis, 4% could represent a relatively small percentage of a population exhibiting a specific characteristic or a small probability of an event occurring. For example, 4% of a survey sample might agree with a particular opinion, or a product might have a 4% defect rate. Understanding this percentage is crucial for interpreting data and making informed decisions.
-
Finance and Investing: In finance, 4% might represent a return on investment, an interest rate, or a change in the value of an asset. For example, a 4% annual interest rate on a savings account would represent a modest yet steady growth.
-
Measurements and Ratios: The fraction could be used to express ratios or proportions in various measurement contexts. For example, a mixture might contain 4% of a specific ingredient.
-
Discounts and Sales: A 4% discount on a product's price is a common occurrence in retail settings.
-
Surveys and Polling: When analyzing survey results, 4% might represent the percentage of respondents who selected a particular option.
V. Expanding the Understanding: Exploring Related Fractions
Understanding 8/200 allows us to explore related fractions and their properties. For instance, consider the fractions 16/400, 24/600, or 32/800. These fractions, when simplified, all reduce to 1/25 or 4%. This highlights the concept of equivalent fractions and demonstrates how different representations can depict the same proportion.
VI. Connecting to Ratios and Proportions
The fraction 8/200 can be interpreted as a ratio, expressing the relationship between two quantities. It shows that for every 200 units of a whole, there are 8 units of a specific part. This concept of ratios and proportions is fundamental in many fields, including chemistry, physics, and engineering, where it's used to determine the relative amounts of different substances or components.
VII. Visualizing the Fraction: A Pictorial Representation
Visual aids can enhance the understanding of fractions. Consider a 100 x 100 grid representing a whole. Shading 4 squares out of the 100 would visually represent 4%, demonstrating the fractional portion compared to the whole. Such visualizations make abstract mathematical concepts more tangible and easier to grasp.
VIII. Beyond the Basics: Advanced Applications
The fraction 8/200 can even serve as a stepping stone to more advanced mathematical concepts. For example, it could be used to illustrate the concept of limits in calculus or to explore infinite series.
IX. Frequently Asked Questions (FAQs)
Q: Can 8/200 be simplified further than 1/25?
A: No. 1/25 is the simplest form of the fraction because the numerator (1) and the denominator (25) share no common divisors other than 1.
Q: What is the reciprocal of 8/200?
A: The reciprocal of a fraction is obtained by swapping the numerator and denominator. The reciprocal of 8/200 (or 1/25) is 25/1, or simply 25.
Q: How do I convert 8/200 to a percentage using a different method?
A: You can also convert 8/200 to a percentage by first simplifying it to 1/25, and then setting up a proportion: 1/25 = x/100. Solving for x, we get x = 4, which means the fraction represents 4%.
Q: Are there any real-world examples of 8/200 being used in a practical context?
A: While not explicitly stated as 8/200, many real-world situations implicitly use this fraction. For example, if a company surveys 200 customers and 8 express dissatisfaction, the dissatisfaction rate is 4%, representing the same proportion as 8/200.
X. Conclusion: The Unassuming Power of 8/200
The seemingly insignificant fraction 8/200 reveals a depth of mathematical concepts and practical applications. Through simplification, decimal conversion, percentage equivalence, and real-world examples, we've uncovered its significance. Understanding this fraction allows us to build a more solid foundation in mathematics and appreciate its relevance in various fields. It's a testament to the power of seemingly simple mathematical concepts and their ability to reveal insights into the world around us. The journey of understanding 8/200 isn't just about solving a fraction; it's about enhancing our numerical literacy and problem-solving abilities. This seemingly small fraction holds a significant educational value, encouraging a deeper exploration of fundamental mathematical principles.
Latest Posts
Latest Posts
-
128kg In Lbs
Sep 20, 2025
-
Water In Pitcher
Sep 20, 2025
-
Social Value Definition
Sep 20, 2025
-
God Of Gravity
Sep 20, 2025
-
20 Of 88
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 8 Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.