8/11 In Decimal
interactiveleap
Sep 23, 2025 · 5 min read
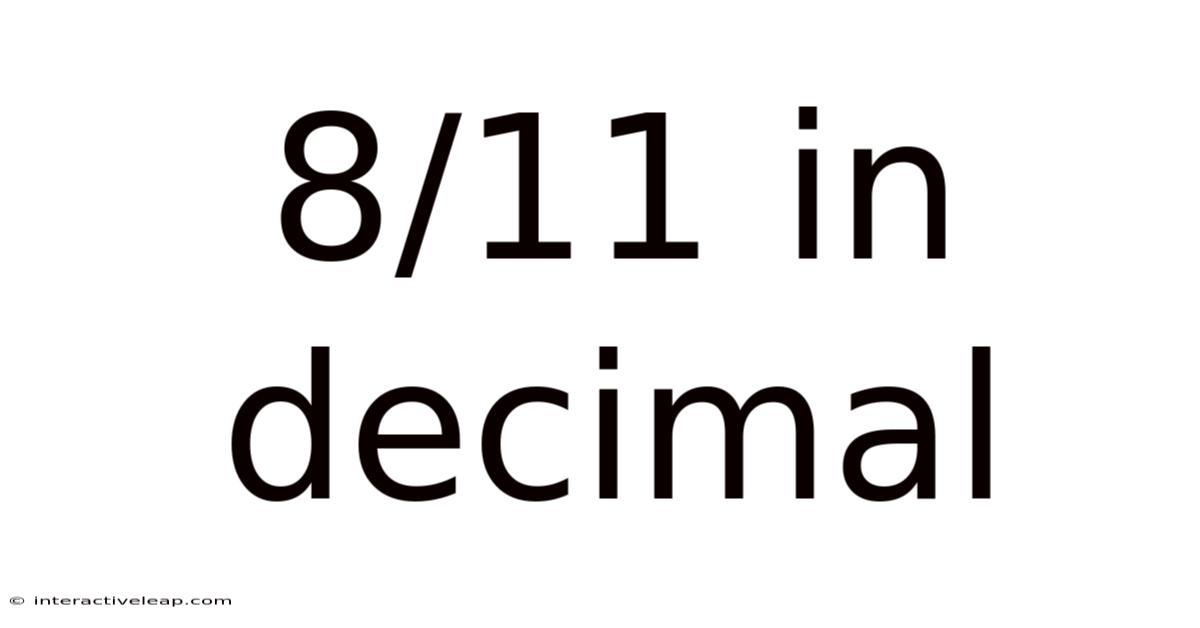
Table of Contents
Unveiling the Mystery: Understanding 8/11 in Decimal Form
The seemingly simple fraction 8/11 presents a fascinating challenge when converting it to its decimal equivalent. While some fractions yield neat, terminating decimals, 8/11 reveals a repeating decimal pattern, leading us on a journey into the world of rational numbers and their representation. This comprehensive guide will not only show you how to convert 8/11 to decimal but will also explore the underlying mathematical concepts, provide practical methods for handling similar conversions, and address frequently asked questions. By the end, you'll have a deep understanding of this seemingly simple yet surprisingly complex fraction.
Understanding Fractions and Decimals
Before diving into the conversion process, let's establish a solid foundation. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many parts make up the whole.
A decimal is another way to represent a fraction, using a base-ten system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. Decimals can be either terminating (ending after a finite number of digits) or repeating (having a sequence of digits that repeats indefinitely).
Converting 8/11 to Decimal: The Long Division Method
The most fundamental method for converting a fraction to a decimal is through long division. We divide the numerator (8) by the denominator (11):
0.727272...
11 | 8.000000
-7.7
-----
0.30
-22
-----
0.80
-77
-----
0.30
-22
-----
0.80
...and so on
As you can see, the division process results in a repeating pattern: 72. This means that the decimal representation of 8/11 is 0.727272... We can represent this repeating decimal using a bar notation: 0.72
Understanding Repeating Decimals
The repeating nature of the decimal representation of 8/11 is a key characteristic of rational numbers. A rational number is any number that can be expressed as a fraction of two integers (where the denominator is not zero). Rational numbers always have either terminating or repeating decimal representations. Irrational numbers, on the other hand, like π (pi) or the square root of 2, have non-repeating, non-terminating decimal representations.
The repeating block in 0.72 is called the repetend. The length of the repetend is called the period. In this case, the period is 2.
Alternative Methods for Conversion
While long division is the most direct approach, other methods can assist in converting fractions to decimals, especially when dealing with more complex fractions. These methods rely on understanding the relationship between fractions and decimals:
-
Converting to equivalent fractions with denominators that are powers of 10: This approach involves finding an equivalent fraction with a denominator of 10, 100, 1000, etc. While this is not always possible (as is the case with 8/11), it’s a helpful technique for fractions that can be simplified this way. For example, 1/2 = 5/10 = 0.5.
-
Using a calculator: Most calculators can readily convert fractions to decimals. Simply input the fraction (8/11) and the calculator will provide the decimal equivalent. However, remember that calculators often truncate or round repeating decimals, so you may not see the entire repeating pattern.
-
Understanding fraction simplification: Before converting, it's crucial to simplify the fraction to its lowest terms. Simplifying reduces the complexity of the long division process.
The Significance of Repeating Decimals in Mathematics
Repeating decimals are not simply an anomaly; they hold significant mathematical importance:
-
Representation of Rational Numbers: As mentioned earlier, all rational numbers have either terminating or repeating decimal expansions. This fact forms the basis for numerous mathematical proofs and theorems.
-
Geometric Series: Repeating decimals can be elegantly expressed as the sum of an infinite geometric series. This connection allows for the manipulation and analysis of repeating decimals using powerful mathematical tools.
-
Applications in Computer Science: Representing and manipulating repeating decimals within computer systems requires careful consideration of precision and potential rounding errors. Understanding the underlying mathematics is crucial for developing robust algorithms.
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals is vital in many real-world applications:
-
Measurement and Engineering: Precise measurements often require converting fractions (e.g., inches) to decimals for calculations and comparisons.
-
Finance and Accounting: Dealing with percentages and monetary values frequently necessitates the conversion of fractions to decimals.
-
Data Analysis and Statistics: Data analysis often involves handling fractions, and converting them to decimals is crucial for statistical calculations and visualizations.
Frequently Asked Questions (FAQ)
Q: Why does 8/11 produce a repeating decimal?
A: 8/11 produces a repeating decimal because 11 is not a factor of any power of 10 (10, 100, 1000, etc.). Only fractions whose denominators can be expressed as a product of 2s and 5s will result in a terminating decimal.
Q: How can I express 0.727272... accurately without using the bar notation?
A: While the bar notation is the most concise way to represent a repeating decimal, you could also write it as 0.72 with an ellipsis (...) to indicate the repetition. However, this is less precise than the bar notation. Mathematically, it is often represented using an infinite geometric series.
Q: Are there any tricks for quickly recognizing fractions that will result in repeating decimals?
A: While there's no foolproof shortcut, a good indicator is if the denominator of the fraction, in its simplest form, contains prime factors other than 2 and 5.
Q: What happens if I use a calculator to convert 8/11 to a decimal and it gives me a slightly different result?
A: Calculators often have limitations on the number of digits they can display. They might truncate or round the repeating decimal, leading to a slightly inaccurate result. The true decimal representation is 0.727272... repeating infinitely.
Conclusion
Converting the fraction 8/11 to its decimal equivalent—0.72—might seem a straightforward task, but it unlocks a deeper understanding of rational numbers, repeating decimals, and their significance in mathematics and various real-world applications. By mastering the long division method and exploring the underlying mathematical concepts, you gain valuable skills applicable to diverse fields, from precise engineering calculations to financial analysis. The seemingly simple fraction 8/11 serves as a gateway to a richer understanding of the elegant interconnectedness within the world of numbers. Remember, practice makes perfect! The more you work with fractions and decimals, the more confident and efficient you will become in converting between these essential mathematical representations.
Latest Posts
Latest Posts
-
Formula Sodium Sulfide
Sep 23, 2025
-
Massive Tennis Ball
Sep 23, 2025
-
1 5 Of 70
Sep 23, 2025
-
46 9kg In Stone
Sep 23, 2025
-
Restaurant In Portuguese
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 8/11 In Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.