8/10 In Percentage
interactiveleap
Sep 22, 2025 · 5 min read
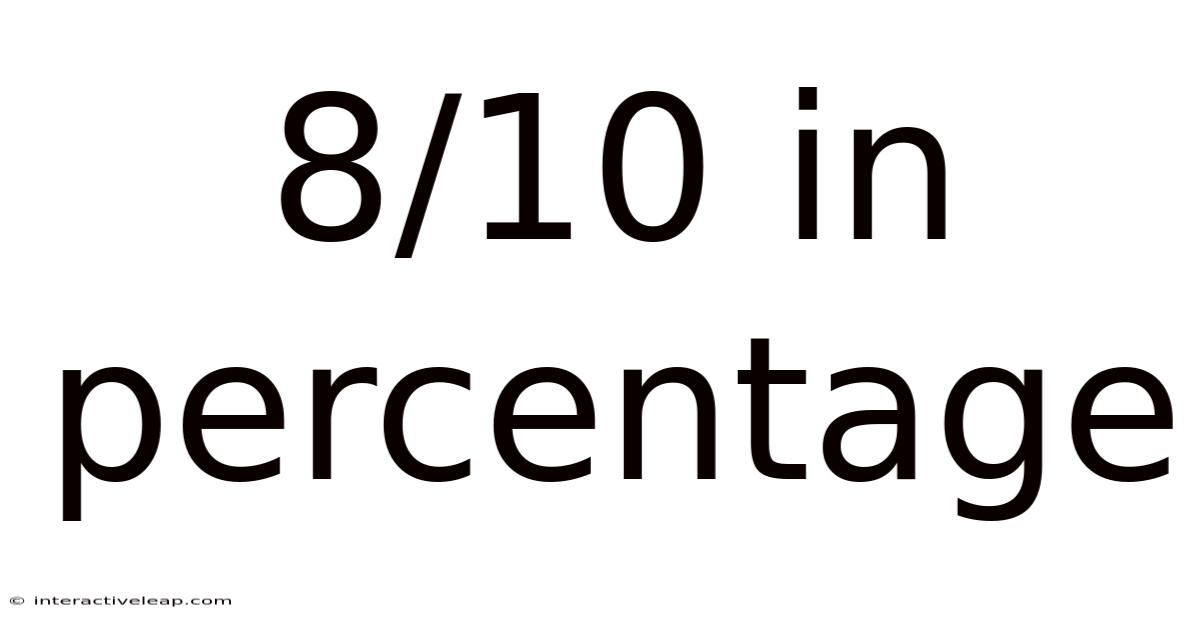
Table of Contents
Decoding 8/10: Understanding Fractions, Decimals, and Percentages
What does 8/10 mean? It's more than just a fraction; it represents a part of a whole, a concept fundamental to mathematics and applicable across numerous real-world scenarios. This comprehensive guide will delve into the meaning of 8/10, explore its representation as a decimal and percentage, and provide practical applications to solidify your understanding. Understanding fractions, decimals, and percentages is crucial for various fields, from finance and statistics to everyday tasks like calculating discounts and tips. Learn how to easily convert between these formats and master this essential mathematical skill.
Understanding Fractions: The Building Blocks
A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). In the fraction 8/10, 8 is the numerator and 10 is the denominator. The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. Think of a pizza cut into 10 slices; 8/10 represents eating 8 out of those 10 slices.
Fractions can be simplified by finding the greatest common divisor (GCD) of both the numerator and the denominator. The GCD is the largest number that divides both numbers without leaving a remainder. In the case of 8/10, the GCD is 2. Dividing both the numerator and denominator by 2 simplifies the fraction to 4/5. This doesn't change the value; it simply represents the same proportion in a more concise form.
Converting Fractions to Decimals: A Simple Process
Converting a fraction to a decimal involves dividing the numerator by the denominator. For 8/10, you would perform the calculation 8 ÷ 10. This results in 0.8. Decimals are another way to represent parts of a whole, using a base-10 system. The number to the left of the decimal point represents whole units, while the digits to the right represent fractions of a unit. 0.8 indicates eight-tenths of a whole.
This conversion process is straightforward for most fractions. However, some fractions result in repeating decimals, where the decimal digits repeat infinitely. For instance, 1/3 converts to 0.3333... Understanding both terminating and repeating decimals is crucial for accurate calculations and interpretations.
Converting Fractions and Decimals to Percentages: Expressing Proportions
A percentage is a way of expressing a number as a fraction of 100. It uses the percent symbol (%). To convert a decimal to a percentage, multiply the decimal by 100 and add the % symbol. Therefore, 0.8 (the decimal equivalent of 8/10) becomes 80%. This signifies that 8/10 represents 80 parts out of 100.
Similarly, to convert a fraction directly to a percentage, you can first convert the fraction to a decimal and then multiply by 100. Alternatively, you can set up a proportion:
Fraction/1 = x/100
Solving for x will give you the percentage equivalent. For 8/10:
8/10 = x/100
Cross-multiplying: 10x = 800
Dividing by 10: x = 80
Therefore, 8/10 is equal to 80%.
Real-World Applications of 8/10 (80%)
The concept of 8/10, or 80%, is frequently encountered in various real-life situations:
- Academic Performance: A score of 8/10 on a test indicates a strong understanding of the material, representing 80% accuracy.
- Sales and Discounts: A store offering an 80% discount means you pay only 20% of the original price.
- Surveys and Polls: 80% of respondents agreeing to a particular statement highlights significant support.
- Financial Investments: An 80% return on investment represents a substantial profit.
- Project Completion: 80% project completion signifies significant progress toward the final goal.
Beyond the Basics: Deeper Understanding of Percentages
Understanding percentages goes beyond simple conversions. Here are some more advanced concepts:
- Percentage Increase/Decrease: Calculating the percentage change between two values involves finding the difference, dividing by the original value, and multiplying by 100. For example, if a price increases from $10 to $18, the percentage increase is ((18-10)/10) * 100 = 80%.
- Percentage of a Number: Finding a percentage of a number involves multiplying the number by the percentage (expressed as a decimal). For instance, 80% of 50 is 0.8 * 50 = 40.
- Compound Interest: This involves calculating interest not only on the principal amount but also on the accumulated interest. Compound interest calculations are essential in finance and investing.
Frequently Asked Questions (FAQs)
Q1: How do I convert a percentage back to a fraction?
A1: Divide the percentage by 100 and simplify the resulting fraction. For example, 80% becomes 80/100, which simplifies to 4/5.
Q2: Can a percentage be greater than 100%?
A2: Yes, a percentage can exceed 100% if the value being represented is larger than the reference value. This often occurs when comparing changes or growth rates.
Q3: Why are percentages useful?
A3: Percentages provide a standardized way to compare proportions and make comparisons easier to understand. They facilitate communication about relative sizes and changes.
Q4: What are some common errors when working with percentages?
A4: Common errors include incorrect placement of the decimal point during conversions, misinterpreting percentage increases/decreases, and failing to account for compounding effects.
Q5: How can I improve my understanding of fractions, decimals, and percentages?
A5: Practice is key. Solve numerous conversion problems, work on real-world applications, and use online resources or educational materials for further learning.
Conclusion: Mastering the Power of 8/10 and Beyond
8/10, or 80%, is a fundamental concept in mathematics with widespread real-world applications. Understanding how to convert between fractions, decimals, and percentages is a crucial skill for numerous fields and everyday life. This guide provided a comprehensive overview of these concepts, demonstrated practical applications, and addressed common questions. By mastering these skills, you'll gain a deeper understanding of proportions, comparisons, and mathematical reasoning, empowering you to confidently navigate quantitative information in any context. Remember, consistent practice and a curious mind are the keys to mastering this essential mathematical skillset. Keep exploring, keep learning, and you'll find the world of numbers increasingly accessible and rewarding.
Latest Posts
Latest Posts
-
Rhyme Of Dreams
Sep 22, 2025
-
62in In Cm
Sep 22, 2025
-
3 35kg To Pounds
Sep 22, 2025
-
Basketball On Head
Sep 22, 2025
-
4 25 As Decimal
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 8/10 In Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.