75 Of 85
interactiveleap
Sep 19, 2025 · 6 min read
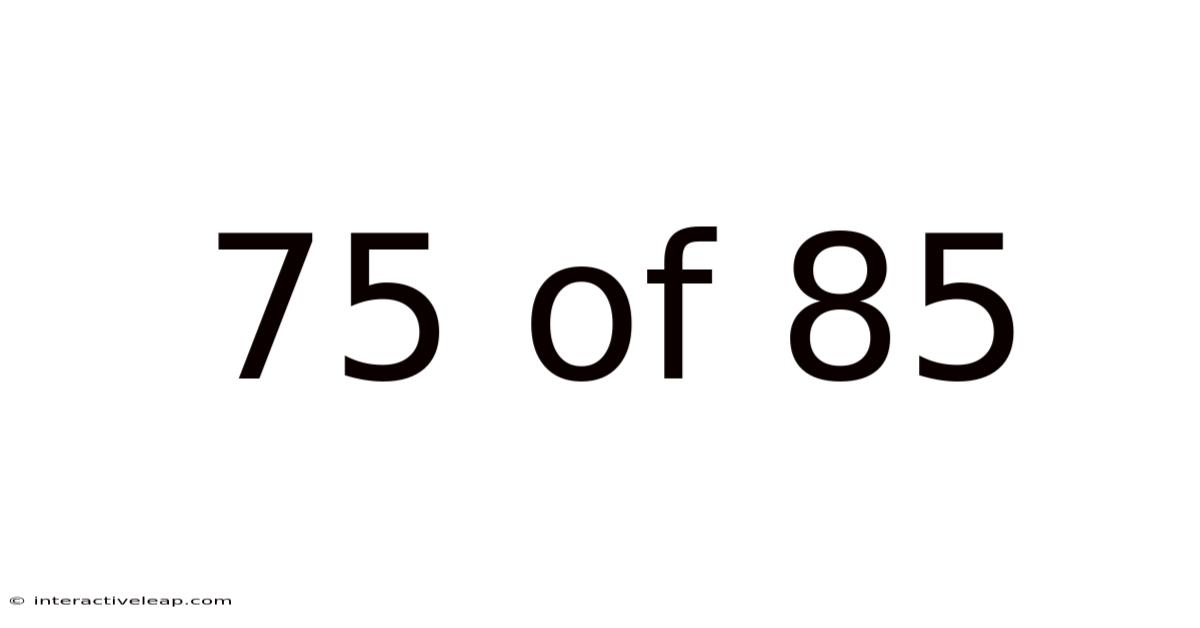
Table of Contents
Understanding the Significance of 75 out of 85: A Deep Dive into Percentages, Proportions, and Applications
What does 75 out of 85 truly mean? This seemingly simple question opens the door to a world of mathematical concepts, including percentages, proportions, ratios, and their practical applications in various fields. This article will delve deep into understanding this specific fraction, exploring its calculation, interpretation, and relevance in everyday life and specialized contexts. We'll move beyond simple percentage calculations to explore the underlying mathematical principles and real-world scenarios where this type of calculation becomes crucial.
Introduction: Deconstructing the Fraction 75/85
The fraction 75/85 represents a part-to-whole relationship. It signifies that 75 units are present out of a total of 85 units. Understanding this relationship is fundamental to interpreting its meaning in different contexts. This fraction can be expressed in various ways, each offering a different perspective on the data:
- Fraction: 75/85
- Decimal: Approximately 0.882
- Percentage: Approximately 88.2%
- Ratio: 75:85 (which can be simplified to 15:17)
Each representation provides valuable information, allowing for different interpretations depending on the situation and the audience. The percentage representation, approximately 88.2%, is often the most easily understood and widely used representation in everyday communication.
Calculating the Percentage: A Step-by-Step Guide
Converting the fraction 75/85 to a percentage involves a straightforward calculation:
-
Divide the numerator by the denominator: 75 ÷ 85 = 0.88235 (approximately)
-
Multiply the result by 100: 0.88235 × 100 = 88.235%
-
Round to the desired precision: In most cases, rounding to one decimal place (88.2%) is sufficient for clarity.
This simple calculation gives us the percentage representation of 75 out of 85, revealing that 75 represents approximately 88.2% of the total 85 units. This percentage is a crucial piece of information for interpreting the data's significance.
Interpreting the Results: Context Matters
The interpretation of 88.2% depends entirely on the context. Here are a few examples illustrating the variety of interpretations:
-
Academic Performance: If 75 represents the number of correct answers out of 85 questions on a test, an 88.2% score suggests a strong understanding of the subject matter. However, the significance would vary depending on the grading scale and the overall class performance.
-
Manufacturing Quality Control: If 75 out of 85 manufactured items pass quality control, the 88.2% pass rate might indicate a high-quality production process. However, a deeper investigation might be required if the 10 failures represent a critical component or a specific manufacturing flaw.
-
Sales Performance: If a salesperson achieved 75 sales out of 85 potential clients, the 88.2% conversion rate demonstrates impressive sales performance. Analyzing the reasons for the 10 unsuccessful sales could lead to further sales improvements.
-
Survey Results: If 75 out of 85 respondents answered "yes" to a survey question, the 88.2% positive response indicates a strong agreement with the statement. However, understanding the sample size and potential biases in the survey is crucial for a valid interpretation.
The Importance of Proportions and Ratios
Understanding 75 out of 85 goes beyond simply calculating the percentage. The concepts of proportion and ratio provide deeper insights into the relationship between the parts and the whole.
A proportion states that two ratios are equal. In this case, we can set up the proportion:
75/85 = x/100
Solving for x (the percentage) gives us the same result as before: x ≈ 88.2%.
A ratio is a comparison of two quantities. The ratio of correct answers to incorrect answers is 75:10, which simplifies to 15:2. This ratio provides a different perspective on the data, focusing on the relationship between successes and failures rather than the overall percentage.
Understanding both proportions and ratios allows for a more nuanced interpretation of the data, providing a more complete picture of the situation.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
The fraction 75/85 can be simplified by finding the greatest common divisor (GCD) of 75 and 85. The GCD of 75 and 85 is 5. Dividing both the numerator and denominator by 5, we get the simplified fraction 15/17. This simplified fraction represents the same proportion but is easier to work with in certain contexts.
Advanced Applications: Statistical Inference and Hypothesis Testing
In statistical analysis, understanding proportions like 75/85 is fundamental. These proportions can be used to:
-
Estimate population parameters: If the 85 units represent a sample from a larger population, the proportion 75/85 can be used to estimate the proportion in the entire population. This estimation is subject to sampling error, but statistical methods can quantify this uncertainty.
-
Conduct hypothesis tests: Researchers might use this proportion to test hypotheses about population proportions. For example, they might test whether the observed proportion of 88.2% is significantly different from a hypothesized value (e.g., 90%). Statistical tests, such as z-tests or chi-square tests, are used to determine the statistical significance of the results.
Real-World Examples Across Different Disciplines
The concept of 75 out of 85, and its percentage equivalent, finds application in a wide array of disciplines:
-
Medicine: Clinical trial success rates, patient response to treatments, and disease prevalence are often expressed as percentages, reflecting a part-to-whole relationship similar to 75/85.
-
Finance: Investment returns, market share, and risk assessment often rely on proportional calculations to understand financial performance and predict future trends.
-
Engineering: Quality control in manufacturing, reliability testing, and performance evaluation often employ percentages to express the success or failure rates of systems and components.
-
Environmental Science: Species survival rates, pollution levels, and resource depletion are often represented as percentages or proportions to communicate environmental trends and inform conservation efforts.
Frequently Asked Questions (FAQ)
Q1: How do I calculate the percentage error in this calculation?
A1: Calculating the percentage error requires knowing the true value. Since we're dealing with an observed proportion, there isn't a true value to compare against. The error arises from rounding and sampling if this proportion is part of a larger data set. More advanced statistical methods would address this.
Q2: What if the denominator is zero?
A2: A denominator of zero is undefined. It represents a situation where there is no total, making a percentage calculation impossible.
Q3: Can this be applied to situations with more than two categories?
A3: Yes! The principles of proportions and percentages can be extended to situations with multiple categories. For example, you could have several categories of responses in a survey, each represented as a proportion of the total number of respondents.
Q4: What software can I use to perform these calculations easily?
A4: Most spreadsheet software (like Microsoft Excel or Google Sheets) and scientific calculators can easily perform these calculations.
Conclusion: Beyond the Numbers
Understanding the significance of 75 out of 85 extends far beyond a simple percentage calculation. It involves a deeper comprehension of fractions, proportions, ratios, and their application in diverse contexts. This article aimed to not only provide a clear and step-by-step guide to calculating the percentage but also to emphasize the broader mathematical and practical implications of understanding these concepts. Mastering these fundamentals forms a strong foundation for more advanced mathematical and statistical applications, crucial for success in various fields of study and professional pursuits. Remember, while the percentage provides a concise representation of the data, the context and further analysis are crucial for making informed decisions and drawing meaningful conclusions.
Latest Posts
Latest Posts
-
83 Times Table
Sep 19, 2025
-
5 Of 5million
Sep 19, 2025
-
85 Of 70
Sep 19, 2025
-
81 65kg In Stone
Sep 19, 2025
-
Cl To Liters
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 85 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.