75 Of 48
interactiveleap
Sep 14, 2025 · 6 min read
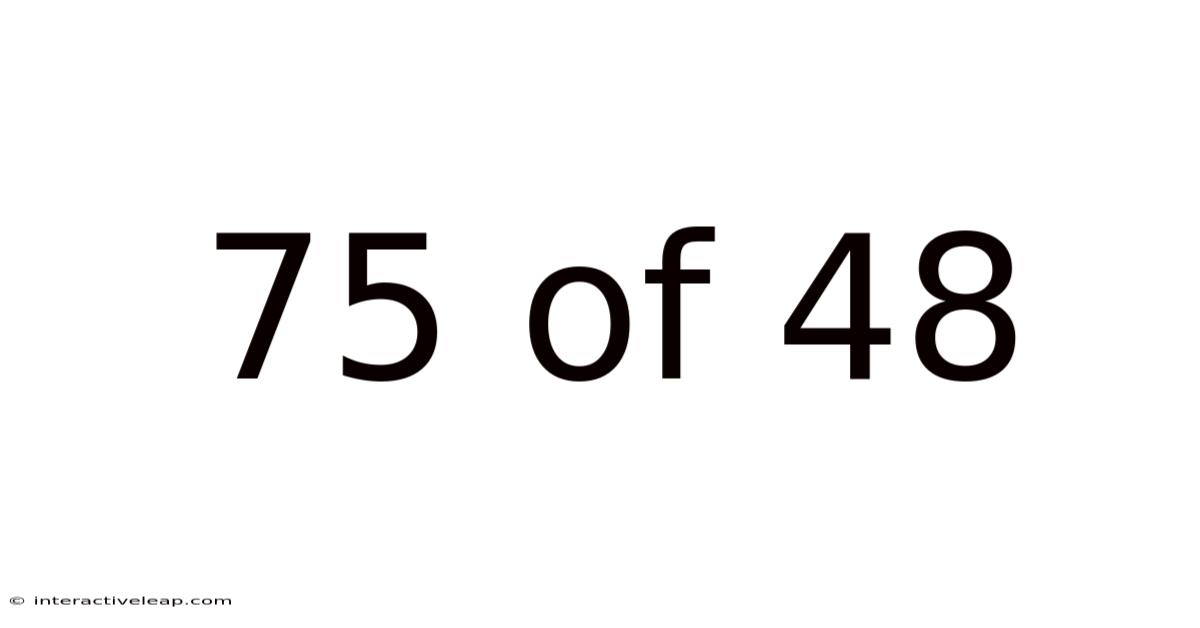
Table of Contents
Understanding the Fraction 75/48: Simplification, Decimal Conversion, and Real-World Applications
This article delves into the seemingly simple fraction 75/48, exploring its simplification, decimal equivalent, and practical applications. We'll move beyond basic calculations to understand the underlying mathematical concepts and how this fraction can be used to solve real-world problems. This comprehensive guide will equip you with a deeper understanding of fractions, making you more confident in tackling similar mathematical challenges.
I. Simplifying the Fraction 75/48
The fraction 75/48 represents a ratio of 75 parts to 48 parts. Before we delve into more complex operations, let's simplify this fraction to its lowest terms. Simplification involves finding the greatest common divisor (GCD) of both the numerator (75) and the denominator (48) and dividing both by it.
The prime factorization of 75 is 3 x 5 x 5, or 3 x 5². The prime factorization of 48 is 2 x 2 x 2 x 2 x 3, or 2⁴ x 3.
The greatest common divisor of 75 and 48 is 3. Dividing both the numerator and the denominator by 3, we get:
75 ÷ 3 = 25 48 ÷ 3 = 16
Therefore, the simplified form of 75/48 is 25/16. This simplified fraction represents the same ratio as 75/48 but is expressed in a more concise and manageable form. This simplification makes further calculations and comparisons much easier.
II. Converting 75/48 (or 25/16) to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case, we will use the simplified fraction 25/16 for easier calculation.
25 ÷ 16 = 1.5625
Therefore, the decimal equivalent of 75/48 is 1.5625. This decimal representation provides an alternative way to understand and work with the ratio. Understanding both the fractional and decimal forms allows for flexibility in different mathematical contexts.
III. Understanding Improper Fractions and Mixed Numbers
Notice that both 75/48 and its simplified form, 25/16, are improper fractions. This means the numerator is larger than the denominator. Improper fractions can be converted into mixed numbers, which combine a whole number and a proper fraction.
To convert 25/16 to a mixed number, we divide the numerator (25) by the denominator (16):
25 ÷ 16 = 1 with a remainder of 9
This means that 25/16 is equal to 1 9/16. The whole number '1' represents the number of times 16 goes into 25 completely, while 9/16 represents the remaining fraction.
IV. Real-World Applications of 75/48 (and its equivalents)
While 75/48 might seem like an abstract mathematical concept, it can represent various real-world scenarios. Here are a few examples:
-
Measurement and Proportions: Imagine you're working with a blueprint where a certain length is represented by 75 units on the plan, but the actual length is 48 units. The ratio 75/48 (or 25/16) represents the scale of the blueprint. You can use this ratio to calculate the actual dimensions of other elements on the blueprint.
-
Resource Allocation: Suppose a team of 48 workers needs to complete a project requiring 75 hours of total work. The fraction 75/48 represents the average number of hours each worker needs to contribute. This understanding is crucial for proper task assignment and time management.
-
Financial Calculations: Imagine you're analyzing the performance of an investment. If your initial investment is 48 units and your current value is 75 units, the fraction 75/48 represents the growth factor of your investment. This ratio allows you to understand the percentage increase in your investment's value.
-
Recipe Adjustments: If a recipe calls for 48 units of a particular ingredient and you want to make a larger batch using 75 units, the fraction 75/48 helps determine the scaling factor for all other ingredients in the recipe.
-
Data Analysis and Statistics: In statistical analysis, you often deal with ratios and proportions. 75/48 could represent the ratio of favorable outcomes to total outcomes in a particular experiment.
V. Further Exploration: Percentage Representation
To fully understand the fraction 75/48, let's express it as a percentage. Remember that a percentage is a fraction with a denominator of 100. To convert 25/16 to a percentage, we first convert it to a decimal (1.5625) and then multiply by 100:
1.5625 x 100 = 156.25%
This indicates that 75 is 156.25% of 48. This percentage representation is useful for expressing the relationship between the two numbers in a way that's easily understood in many contexts.
VI. Frequently Asked Questions (FAQ)
Q: Can 75/48 be further simplified beyond 25/16?
A: No. 25 and 16 share no common divisors other than 1, meaning 25/16 is the fraction in its simplest form.
Q: What is the difference between an improper fraction and a mixed number?
A: An improper fraction has a numerator larger than its denominator (e.g., 75/48). A mixed number combines a whole number and a proper fraction (e.g., 1 9/16). They represent the same value, just in different forms.
Q: Why is simplification important in working with fractions?
A: Simplification makes calculations easier, reduces the risk of errors, and allows for clearer comparisons between fractions. A simplified fraction is more manageable and easier to interpret.
Q: What are some other ways to represent the ratio 75:48?
A: Besides fractions, decimals, and percentages, the ratio can be represented as a scale (e.g., 75:48), as a proportion (e.g., 75/123 = x/100 where x represents the percentage), or graphically (e.g., using a bar graph or pie chart).
Q: Are there online tools to help simplify fractions and perform conversions?
A: Yes, numerous online calculators and tools are available to simplify fractions, convert them to decimals and percentages, and perform other fraction-related calculations. These tools can be helpful for checking your work and improving your understanding.
VII. Conclusion
This in-depth exploration of the fraction 75/48 reveals that a seemingly simple fraction can unveil a wealth of mathematical concepts and real-world applications. By understanding the process of simplification, decimal conversion, and the different ways to represent this ratio (as an improper fraction, mixed number, or percentage), you gain a much stronger foundation in fractional arithmetic. This knowledge is transferable to many areas, from basic math to advanced subjects like algebra, geometry, and calculus. Remember that practicing these concepts regularly is key to developing proficiency and confidence in working with fractions and ratios. The more you practice, the more comfortable and intuitive these calculations will become. The ability to understand and manipulate fractions is an essential skill that will serve you well in various academic and professional pursuits.
Latest Posts
Latest Posts
-
95 9kg In Stones
Sep 14, 2025
-
83 Km Miles
Sep 14, 2025
-
Factors Influence Supply
Sep 14, 2025
-
Lt To Lbs
Sep 14, 2025
-
3 15 Simplified
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.