75 Of 420
interactiveleap
Sep 24, 2025 · 4 min read
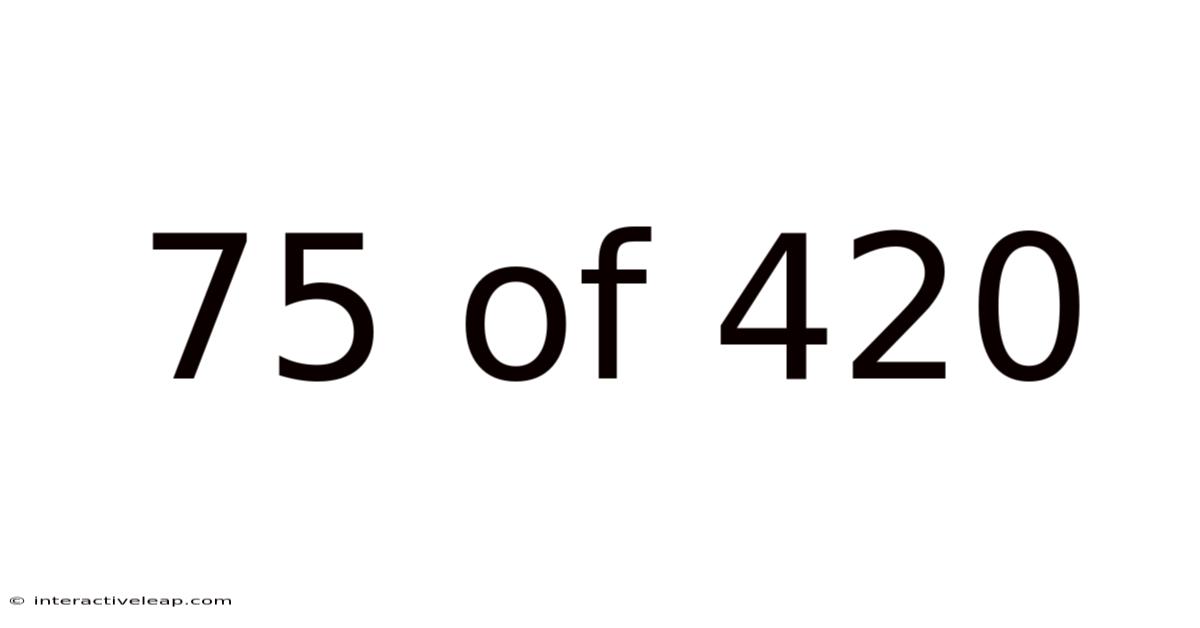
Table of Contents
Deconstructing 75/420: Understanding the Fraction and Its Implications
The fraction 75/420, seemingly simple at first glance, offers a rich opportunity to explore various mathematical concepts and delve into its practical applications. This article will not only simplify the fraction but also unpack its meaning within the context of percentages, ratios, and its potential relevance in various fields, like statistics or even everyday life scenarios. We'll cover simplification, conversion to decimals and percentages, and explore the practical implications of understanding this particular fraction.
Understanding the Basics: Simplifying the Fraction
Before delving into more complex aspects, let's start with the fundamental step of simplifying the fraction 75/420. Simplifying a fraction means reducing it to its lowest terms, expressing it in its most concise form. This is achieved by finding the greatest common divisor (GCD) of both the numerator (75) and the denominator (420) and dividing both by it.
The prime factorization method is a reliable way to find the GCD. Let's break down 75 and 420 into their prime factors:
- 75: 3 x 5 x 5 = 3 x 5²
- 420: 2 x 2 x 3 x 5 x 7 = 2² x 3 x 5 x 7
The common prime factors are 3 and 5. Therefore, the GCD is 3 x 5 = 15.
Dividing both the numerator and the denominator by 15, we get:
75 ÷ 15 = 5 420 ÷ 15 = 28
Therefore, the simplified fraction is 5/28. This simplified form is easier to understand and work with in various calculations.
Converting to Decimal and Percentage
Simplified fractions are easier to manipulate, but expressing them as decimals or percentages can offer a different perspective and facilitate comparisons. To convert 5/28 to a decimal, we perform the division:
5 ÷ 28 ≈ 0.1786
Rounding to two decimal places, we get approximately 0.18.
Converting the decimal to a percentage involves multiplying by 100:
0.1786 x 100 ≈ 17.86%
Therefore, 75/420, simplified to 5/28, is approximately 17.86%. This percentage representation is useful for conveying the relative proportion of 75 out of 420.
Real-World Applications and Interpretations
The fraction 75/420, and its simplified form 5/28, can represent various real-world scenarios. Imagine, for example:
-
Test Scores: A student scoring 75 out of 420 points on a test achieved a score of approximately 17.86%. This allows for easy comparison with other students' scores and helps to gauge overall performance.
-
Survey Results: In a survey of 420 people, 75 responded positively to a particular question. The percentage of positive responses is 17.86%, providing a concise summary of public opinion.
-
Inventory Management: If a warehouse holds 420 units of a product and 75 are sold, the fraction 75/420 represents the proportion of the inventory sold. This simplifies stock management and informs ordering decisions.
-
Statistical Analysis: In statistical studies, fractions are often used to represent probabilities or proportions within a sample. The fraction could represent the proportion of a particular characteristic within a larger data set.
Exploring Ratios and Proportions
The fraction 75/420 can also be viewed as a ratio, expressing the relationship between two quantities. The ratio 75:420, or its simplified form 5:28, indicates that for every 28 units of the whole, 5 units possess a specific characteristic or belong to a particular category. This ratio allows for scaling up or down – for example, maintaining the same proportion with larger or smaller quantities.
Expanding the Understanding: Further Mathematical Explorations
While we have focused on the basic simplification and conversion of 75/420, deeper mathematical concepts can be explored.
-
Continued Fractions: The fraction can be expressed as a continued fraction, a representation that offers insights into the fraction's properties and approximations.
-
Modular Arithmetic: Within the field of modular arithmetic, understanding the remainder when the numerator is divided by the denominator is crucial in solving certain types of problems.
-
Complex Fractions: The fraction could be incorporated into more complex calculations, involving other fractions or mathematical operations.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 75/420?
A: The simplest form of 75/420 is 5/28.
Q: How do I convert 75/420 to a percentage?
A: First, simplify the fraction to 5/28. Then, divide 5 by 28 (approximately 0.1786) and multiply by 100 to get approximately 17.86%.
Q: What are some real-world examples of using this fraction?
A: Real-world examples include calculating test scores, analyzing survey results, managing inventory, and representing proportions in statistical analysis.
Q: Can this fraction be represented as a ratio?
A: Yes, it can be represented as the ratio 75:420, or its simplified form 5:28.
Conclusion
The seemingly simple fraction 75/420 provides a gateway to explore various mathematical concepts, from basic simplification to the application of percentages, ratios, and even more advanced mathematical fields. Understanding how to simplify fractions, convert them to decimals and percentages, and interpret their meaning within different contexts is fundamental for anyone working with numerical data, whether in academic studies, professional fields, or everyday life. This exploration of 75/420 highlights the importance of understanding fundamental mathematical concepts and their broad applicability. The ability to manipulate and interpret fractions is a valuable skill that extends far beyond the classroom.
Latest Posts
Latest Posts
-
Durer Melencolia I
Sep 24, 2025
-
Barium Flame Test
Sep 24, 2025
-
Describe Haunted House
Sep 24, 2025
-
70s Punk Style
Sep 24, 2025
-
48 Times 3
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 420 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.