75 Of 220
interactiveleap
Sep 22, 2025 · 6 min read
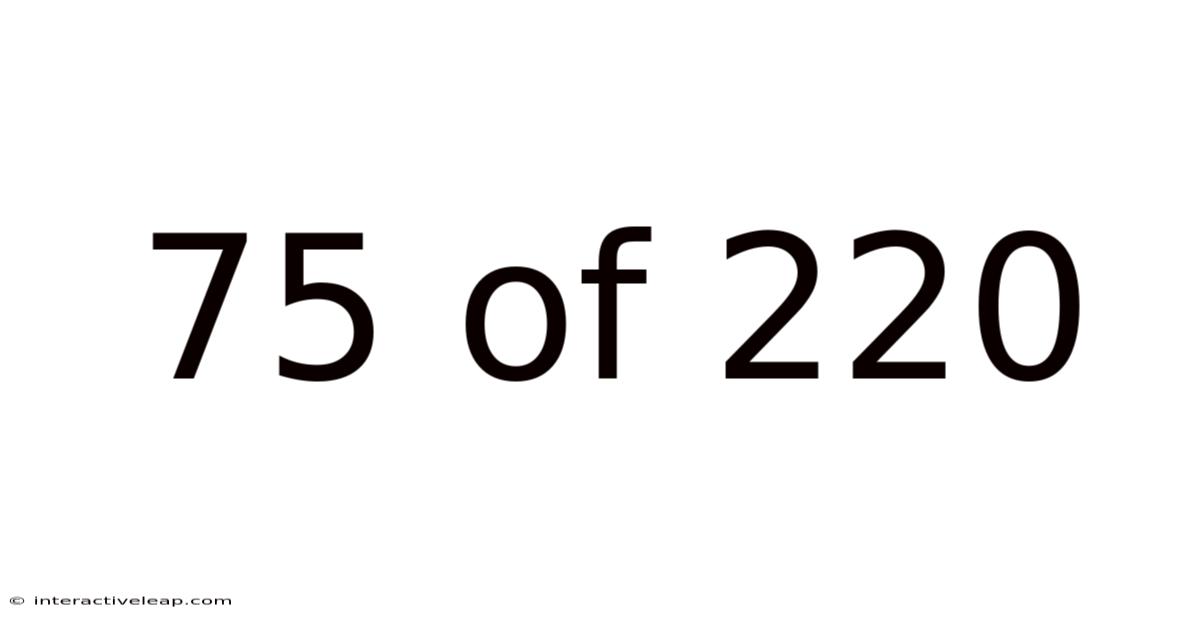
Table of Contents
Decoding the Fraction: Understanding 75/220 and its Implications
The fraction 75/220 might seem insignificant at first glance, just a simple ratio of two numbers. However, understanding this fraction—and how to simplify, interpret, and apply it—opens doors to a deeper understanding of mathematical principles and their real-world applications. This article will delve into the intricacies of 75/220, exploring its simplification, percentage representation, decimal equivalent, and practical applications, ensuring a comprehensive understanding for readers of all mathematical backgrounds.
Introduction: Simplifying Fractions – A Fundamental Skill
Before we embark on a detailed analysis of 75/220, let's refresh our understanding of fraction simplification. Simplifying a fraction, also known as reducing a fraction to its lowest terms, involves finding the greatest common divisor (GCD) of the numerator (75) and the denominator (220) and dividing both by that GCD. This process results in an equivalent fraction that is simpler and easier to work with. This is a crucial skill, not just for academic purposes but also for real-world applications in areas like cooking, construction, and finance.
Finding the Greatest Common Divisor (GCD) of 75 and 220
To simplify 75/220, we need to determine the GCD of 75 and 220. There are several methods to achieve this. One common method is to find the prime factorization of both numbers:
- Prime factorization of 75: 3 x 5 x 5 = 3 x 5²
- Prime factorization of 220: 2 x 2 x 5 x 11 = 2² x 5 x 11
The GCD is the product of the common prime factors raised to the lowest power. In this case, the only common prime factor is 5, and its lowest power is 5¹. Therefore, the GCD of 75 and 220 is 5.
Simplifying 75/220
Now that we know the GCD is 5, we can simplify the fraction:
75 ÷ 5 = 15 220 ÷ 5 = 44
Therefore, the simplified fraction is 15/44. This simplified fraction is equivalent to 75/220, meaning they represent the same proportion or ratio.
Converting the Fraction to a Percentage
Converting a fraction to a percentage involves multiplying the fraction by 100%. Let's convert both the original fraction (75/220) and the simplified fraction (15/44) to percentages:
- 75/220 x 100% ≈ 34.09%
- 15/44 x 100% ≈ 34.09%
As expected, both fractions yield the same percentage, confirming their equivalence. This percentage representation provides a readily understandable way to express the proportion represented by the fraction. For instance, if 75 out of 220 students passed an exam, we can say approximately 34.09% of the students passed.
Converting the Fraction to a Decimal
To convert a fraction to a decimal, we simply divide the numerator by the denominator. Let's do this for both the original and simplified fractions:
- 75 ÷ 220 ≈ 0.3409
- 15 ÷ 44 ≈ 0.3409
Again, we see that both fractions result in the same decimal approximation. The decimal representation is useful for calculations and comparisons, particularly when dealing with other decimal numbers.
Real-World Applications of 75/220 and its Equivalent Fractions
The fraction 75/220, and its simplified form 15/44, has various practical applications across different fields:
-
Statistics and Probability: Imagine a survey where 75 out of 220 respondents answered "yes" to a particular question. The fraction 75/220 (or 15/44) represents the proportion of "yes" responses. This data can be used to analyze trends, make predictions, and draw conclusions.
-
Measurement and Scaling: In construction or engineering, this fraction could represent a ratio of dimensions or materials. For example, it could describe the ratio of the length of a beam to its width.
-
Finance and Budgeting: The fraction could represent a portion of a budget allocated to a specific project or expense.
-
Cooking and Baking: Recipes often involve fractional quantities of ingredients. The fraction could represent the ratio of one ingredient to another in a recipe.
-
Game Theory and Probability: In games of chance, the fraction could represent the probability of a certain event occurring.
Further Exploration: Understanding Ratios and Proportions
The fraction 75/220 is fundamentally a ratio, expressing a relationship between two quantities. Understanding ratios and proportions is crucial for solving a wide range of problems. A proportion is a statement that two ratios are equal. For instance, the proportion 75/220 = 15/44 indicates that the ratios 75:220 and 15:44 are equivalent. Understanding proportions allows us to solve for unknown values in various contexts.
Advanced Concepts: Continued Fractions
While beyond the scope of a basic understanding of 75/220, it's worth mentioning that fractions can be expressed as continued fractions. Continued fractions provide an alternative way to represent rational numbers (fractions) and can be particularly useful in certain mathematical analyses. The continued fraction representation of 15/44 is a relatively straightforward example, offering a deeper insight into the underlying mathematical structure of the fraction.
Frequently Asked Questions (FAQs)
Q1: Is there another way to simplify 75/220 besides using the GCD?
A1: Yes, you can repeatedly divide both the numerator and denominator by common factors until you reach a fraction where there are no more common factors. However, using the GCD is generally the most efficient method.
Q2: Why is simplifying fractions important?
A2: Simplifying fractions makes them easier to understand, compare, and use in calculations. It also ensures consistency and avoids unnecessary complexity.
Q3: Can any fraction be simplified?
A3: Not all fractions can be simplified. If the numerator and denominator have no common factors other than 1, then the fraction is already in its simplest form.
Q4: What if I made a mistake in calculating the GCD?
A4: If you made a mistake in calculating the GCD, your simplified fraction will not be in its lowest terms. You can always double-check your GCD calculation or use a different method to verify the result.
Q5: How can I apply this knowledge to other fractions?
A5: The principles discussed here – finding the GCD, simplifying, converting to percentages and decimals – apply to any fraction. Practice with different fractions will solidify your understanding and improve your skills.
Conclusion: Mastering Fractions – A Building Block for Mathematical Success
The seemingly simple fraction 75/220, when thoroughly examined, reveals a wealth of mathematical concepts and practical applications. Understanding how to simplify fractions, convert them to percentages and decimals, and interpret their meaning is fundamental to mathematical literacy. This knowledge extends far beyond the classroom, finding relevance in various aspects of daily life and professional fields. By mastering these fundamental skills, we build a strong foundation for tackling more complex mathematical problems and enhancing our problem-solving abilities. The journey of understanding 75/220 is not just about the fraction itself; it's about embracing the power of mathematical reasoning and its impact on our world.
Latest Posts
Latest Posts
-
Caramel Dark Chocolate
Sep 22, 2025
-
Wear Wore Worn
Sep 22, 2025
-
80grams To Oz
Sep 22, 2025
-
68 In Pounds
Sep 22, 2025
-
Single Index Model
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 220 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.