75 Of 20
interactiveleap
Sep 16, 2025 · 5 min read
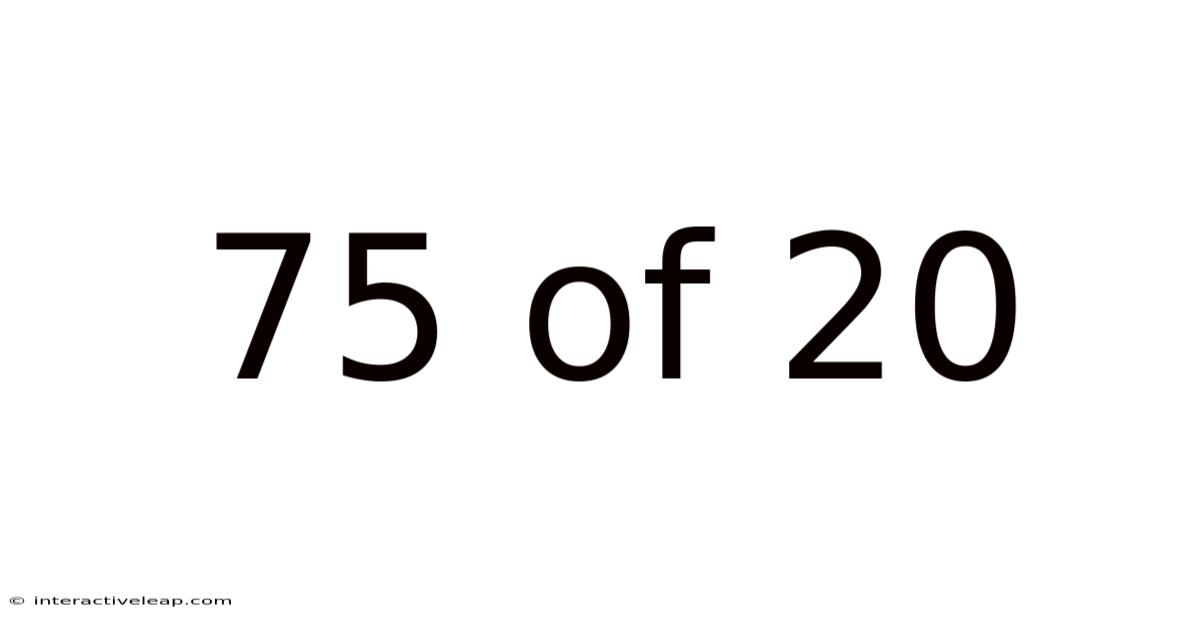
Table of Contents
Decoding the Enigma: Understanding and Mastering the Fraction 75/20
The fraction 75/20 might seem daunting at first glance, but understanding its intricacies unlocks a deeper appreciation for fractions, decimals, and percentages – fundamental concepts in mathematics. This article will guide you through simplifying, converting, and applying this fraction in various contexts, building a strong foundation in mathematical literacy. We'll explore the practical applications and delve into the underlying principles, ensuring you not only solve the problem but also grasp the broader mathematical concepts involved.
Introduction: Why 75/20 Matters
The fraction 75/20, seemingly simple, represents a valuable learning opportunity. Mastering its manipulation helps solidify skills in fraction simplification, decimal conversion, and percentage calculation – skills crucial for various applications, from everyday budgeting to advanced scientific calculations. This seemingly simple fraction serves as a microcosm of the broader mathematical world, providing a hands-on example to understand more complex concepts. Understanding 75/20 isn't just about getting the right answer; it's about developing a deeper understanding of numerical relationships and problem-solving strategies.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before delving into conversions, let's simplify 75/20. Simplification makes the fraction easier to work with and reveals its inherent properties. The key is to find the greatest common divisor (GCD) of both the numerator (75) and the denominator (20). The GCD is the largest number that divides both 75 and 20 without leaving a remainder.
One method to find the GCD is through prime factorization. Let's break down 75 and 20 into their prime factors:
- 75 = 3 x 5 x 5 = 3 x 5²
- 20 = 2 x 2 x 5 = 2² x 5
The common prime factor is 5. Therefore, the GCD of 75 and 20 is 5.
To simplify the fraction, we divide both the numerator and the denominator by the GCD:
75 ÷ 5 = 15 20 ÷ 5 = 4
Therefore, the simplified form of 75/20 is 15/4. This simpler representation retains the same value but is significantly easier to manipulate in further calculations.
Converting to a Decimal: From Fraction to Decimal Representation
Converting 15/4 to a decimal involves performing the division: 15 divided by 4.
15 ÷ 4 = 3.75
Therefore, the decimal equivalent of 75/20 (and its simplified form 15/4) is 3.75. This decimal representation is often preferred for practical applications, particularly when dealing with measurements or monetary values.
Converting to a Percentage: Expressing the Fraction as a Proportion
Converting a fraction to a percentage expresses it as a proportion out of 100. We can start with either the simplified fraction (15/4) or the decimal (3.75).
Method 1: Using the Decimal
Multiply the decimal by 100 to convert it to a percentage:
3.75 x 100 = 375%
Method 2: Using the Fraction
To express 15/4 as a percentage, we need to create an equivalent fraction with a denominator of 100. We can achieve this by finding a number that, when multiplied by 4, equals 100. That number is 25. Therefore, we multiply both the numerator and the denominator by 25:
(15 x 25) / (4 x 25) = 375/100
Since any fraction with a denominator of 100 represents a percentage directly, 375/100 is equal to 375%.
Both methods yield the same result: 75/20 is equivalent to 375%. This high percentage indicates that 75 is significantly greater than 20.
Practical Applications: Real-World Examples of 75/20
The fraction 75/20, and its equivalents, appears in various real-world situations. Consider these examples:
-
Financial Calculations: Imagine you invested $20 and received a return of $75. Your return on investment (ROI) would be 375%, a significant gain.
-
Performance Metrics: If a target was 20 units, and 75 units were achieved, the performance exceeded the target by 375%.
-
Recipe Scaling: If a recipe calls for 20 grams of an ingredient, but you want to make a larger batch, multiplying the ingredient amount by 3.75 (the decimal equivalent) would increase the amount to 75 grams, maintaining the recipe's proportions.
-
Data Analysis: In statistical analysis, percentages and decimal representations are frequently used to represent proportions within datasets. 75/20 could represent a comparison of two data points.
Further Exploration: Understanding Improper Fractions and Mixed Numbers
The fraction 75/20 is an improper fraction because the numerator (75) is larger than the denominator (20). Improper fractions can be converted into mixed numbers, which combine a whole number and a proper fraction.
To convert 15/4 (the simplified form) to a mixed number, we divide the numerator (15) by the denominator (4):
15 ÷ 4 = 3 with a remainder of 3.
This means 15/4 is equal to 3 3/4. This representation indicates three whole units and three-quarters of another unit.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 75/20?
A: The simplest form of 75/20 is 15/4.
Q: How do I convert 75/20 to a decimal?
A: Divide the numerator (75) by the denominator (20). The result is 3.75.
Q: What is 75/20 as a percentage?
A: 75/20 is equal to 375%.
Q: Is 75/20 an improper fraction?
A: Yes, 75/20 is an improper fraction because the numerator is greater than the denominator.
Q: How do I convert 15/4 to a mixed number?
A: Divide 15 by 4. The quotient (3) becomes the whole number, and the remainder (3) becomes the numerator of the fraction, keeping the denominator (4). This results in 3 3/4.
Conclusion: Mastering Fractions – A Foundation for Mathematical Success
Understanding the fraction 75/20, its simplification, conversion to decimals and percentages, and its practical applications provides a solid foundation in fundamental mathematical concepts. The ability to manipulate fractions efficiently is crucial for success in various academic and professional fields. By mastering this seemingly simple fraction, you've taken a significant step towards developing stronger mathematical reasoning skills and a deeper understanding of numerical relationships. Remember that the key is not just in finding the answer, but in understanding the process and applying these skills in diverse contexts. Continue practicing and exploring, and you will build a strong and confident understanding of mathematics.
Latest Posts
Latest Posts
-
43 9kg In Stone
Sep 16, 2025
-
South American Plains
Sep 16, 2025
-
20ml In Tsp
Sep 16, 2025
-
7 3 4
Sep 16, 2025
-
62f In C
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.