75 Of 180
interactiveleap
Sep 13, 2025 · 5 min read
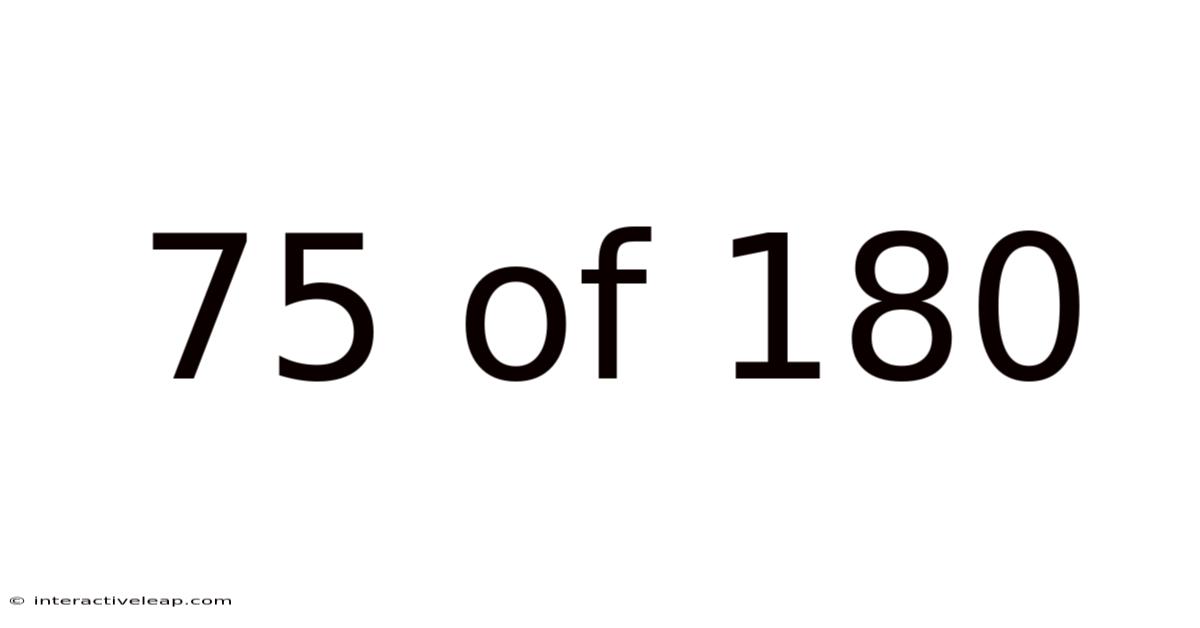
Table of Contents
Decoding the Fraction 75/180: A Comprehensive Guide to Simplification, Decimals, and Percentages
Understanding fractions is a fundamental skill in mathematics, crucial for various aspects of life, from cooking and construction to advanced scientific calculations. This article delves into the fraction 75/180, exploring its simplification, decimal equivalent, percentage representation, and practical applications. We'll break down the process step-by-step, making it accessible to learners of all levels. By the end, you'll not only understand 75/180 but also gain a broader appreciation for working with fractions.
Introduction: What is 75/180?
The fraction 75/180 represents a part of a whole. The number 75 is the numerator, indicating the number of parts we have, while 180 is the denominator, representing the total number of equal parts in the whole. This means we have 75 out of 180 equal parts. Understanding this basic concept is crucial before we proceed to simplification and other representations.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before we delve into decimal and percentage conversions, simplifying the fraction is essential. Simplification involves reducing the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both 75 and 180 without leaving a remainder.
Let's find the GCD of 75 and 180 using the prime factorization method:
- Prime factorization of 75: 3 x 5 x 5 = 3 x 5²
- Prime factorization of 180: 2 x 2 x 3 x 3 x 5 = 2² x 3² x 5
The common factors are 3 and 5. The lowest power of 3 is 3¹ and the lowest power of 5 is 5¹. Therefore, the GCD is 3 x 5 = 15.
Now, we divide both the numerator and the denominator by the GCD:
75 ÷ 15 = 5 180 ÷ 15 = 12
Therefore, the simplified form of 75/180 is 5/12. This simplified fraction is equivalent to the original fraction but is expressed in its most concise form.
Converting the Fraction to a Decimal: Division is Key
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case, we'll use the simplified fraction 5/12 for easier calculation:
5 ÷ 12 = 0.416666...
This decimal representation is a recurring decimal, meaning the digit 6 repeats infinitely. For practical purposes, we can round the decimal to a certain number of decimal places. Rounding to three decimal places, we get 0.417.
Converting the Fraction to a Percentage: Multiplying by 100
To express the fraction as a percentage, we multiply the decimal equivalent by 100. Using the rounded decimal 0.417:
0.417 x 100 = 41.7%
Therefore, 75/180 is equivalent to 41.7% (rounded to one decimal place). This percentage represents the proportion of 75 out of 180 as a percentage of the whole.
Practical Applications of 75/180 (and 5/12)
Understanding fractions like 75/180 and its simplified form, 5/12, has numerous practical applications:
-
Calculating proportions: Imagine you have 180 candies, and 75 of them are chocolate. The fraction 75/180 (or 5/12) represents the proportion of chocolate candies. This can be useful in various scenarios like analyzing survey results, understanding market shares, or even baking!
-
Scaling recipes: If a recipe calls for 12 cups of flour and you only want to make a smaller portion, you can use the fraction 5/12 to scale down the ingredients. Multiplying each ingredient amount by 5/12 will give you the correct proportions for the smaller batch.
-
Financial calculations: Fractions and percentages are essential in financial calculations. For instance, calculating interest rates, discounts, or profit margins often involves working with fractions. Understanding how to convert between fractions, decimals, and percentages is crucial in these situations.
-
Geometric problems: In geometry, fractions often appear in calculations involving areas, volumes, and proportions of shapes. For example, determining the area of a section of a circle or calculating the ratio of sides in similar triangles often involves fractions.
-
Data analysis: Fractions and percentages are vital in presenting and interpreting data. Representing data as fractions or percentages allows for easier understanding and comparison of different proportions.
Further Exploration: Working with Other Fractions
The methods used to simplify, convert to decimals and percentages, and apply 75/180 are applicable to other fractions. Remember these key steps:
-
Find the GCD: Use prime factorization or other methods to find the greatest common divisor of the numerator and denominator.
-
Simplify: Divide both the numerator and denominator by the GCD.
-
Convert to decimal: Divide the numerator by the denominator.
-
Convert to percentage: Multiply the decimal equivalent by 100.
Practice with different fractions to strengthen your understanding and build confidence in working with them.
Frequently Asked Questions (FAQ)
- Q: Why is simplifying a fraction important?
A: Simplifying a fraction makes it easier to understand and work with. It reduces the numbers to their smallest possible values, making calculations more efficient and the results clearer.
- Q: What if I can't find the GCD easily?
A: If you struggle to find the GCD through prime factorization, you can use the Euclidean algorithm, a more systematic approach to finding the GCD of two numbers.
- Q: Is it always necessary to round decimals?
A: Rounding decimals is often necessary for practical applications where exact precision isn't always required. However, in some situations, you might need to keep the exact decimal representation, especially in scientific or engineering calculations.
- Q: Are there other ways to convert fractions to percentages?
A: Yes, you can directly convert a fraction to a percentage by multiplying the fraction by 100%. For example, (75/180) x 100% = 41.666...%
- Q: Can a fraction have a denominator of zero?
A: No, a fraction cannot have a denominator of zero. Division by zero is undefined in mathematics.
Conclusion: Mastering Fractions – A Stepping Stone to Success
Understanding fractions is a cornerstone of mathematical proficiency. This comprehensive exploration of 75/180 demonstrates the practical steps involved in simplifying fractions, converting them to decimals and percentages, and applying them to real-world situations. By mastering these fundamental concepts, you build a solid foundation for more advanced mathematical concepts and problem-solving skills. Remember, consistent practice is key to strengthening your understanding and improving your ability to work confidently with fractions in all their forms. So, grab a pencil, explore different fractions, and enjoy the journey of mastering this essential mathematical skill!
Latest Posts
Latest Posts
-
9 Ft 5
Sep 13, 2025
-
17c To Fahrenheit
Sep 13, 2025
-
165lbs In Kg
Sep 13, 2025
-
121mm In Inches
Sep 13, 2025
-
1600m In Miles
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.