75 Of 18
interactiveleap
Sep 25, 2025 · 5 min read
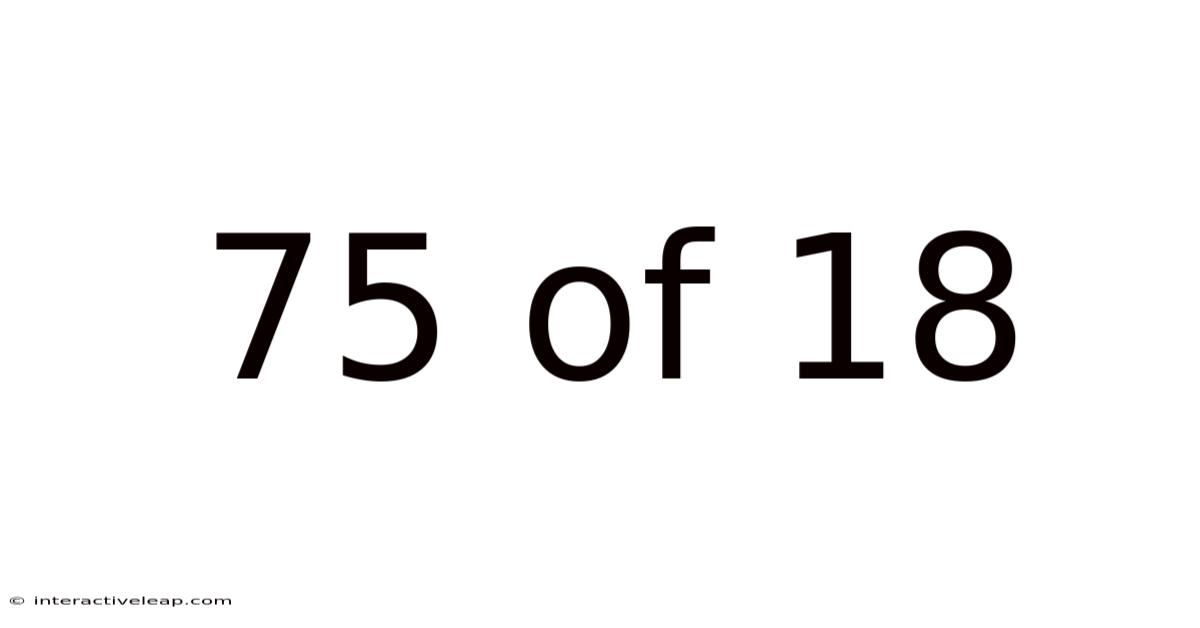
Table of Contents
Understanding the Fraction 75/18: A Comprehensive Guide
The fraction 75/18 might seem daunting at first glance, but understanding its intricacies unlocks a deeper appreciation for mathematical concepts like simplification, improper fractions, and mixed numbers. This comprehensive guide will walk you through various methods of interpreting and working with 75/18, aiming to demystify this seemingly complex fraction and empower you with the skills to tackle similar problems. We'll explore its simplification, conversion to a mixed number, and the underlying mathematical principles involved.
Introduction: What is 75/18?
75/18 represents a ratio or a part of a whole. The number 75 is the numerator (the top number), representing the number of parts we have. The number 18 is the denominator (the bottom number), representing the total number of equal parts that make up the whole. In essence, 75/18 signifies 75 out of 18 equal parts. Because the numerator is larger than the denominator, this is an improper fraction. Understanding this fundamental concept is crucial for further exploration.
Step-by-Step Simplification of 75/18
Simplifying a fraction means reducing it to its lowest terms. This is achieved by finding the greatest common divisor (GCD) of both the numerator and the denominator, and then dividing both by that GCD. Let's find the GCD of 75 and 18:
- Find the factors of 75: 1, 3, 5, 15, 25, 75
- Find the factors of 18: 1, 2, 3, 6, 9, 18
- Identify the common factors: 1 and 3
- The greatest common factor (GCF) is 3.
Now, we divide both the numerator and the denominator by 3:
75 ÷ 3 = 25 18 ÷ 3 = 6
Therefore, the simplified form of 75/18 is 25/6. This simplified fraction retains the same value as the original fraction, just expressed in its most concise form.
Converting 75/18 to a Mixed Number
An improper fraction (like 75/18 or its simplified form 25/6) can be expressed as a mixed number. A mixed number combines a whole number and a proper fraction. To convert 25/6 to a mixed number, we perform division:
- Divide the numerator (25) by the denominator (6): 25 ÷ 6 = 4 with a remainder of 1.
- The quotient (4) becomes the whole number part of the mixed number.
- The remainder (1) becomes the numerator of the fractional part.
- The denominator remains the same (6).
Therefore, 25/6 as a mixed number is 4 1/6. This means that 25/6 represents four whole units and one-sixth of another unit.
Visual Representation of 75/18
Visualizing fractions can aid understanding. Imagine you have 18 equal slices of pizza. 75/18 means you have 75 of these slices. Since you only have 18 slices in total, this represents more than one whole pizza. Simplifying the fraction to 25/6 helps visualize this better: you have 25 slices of a pizza cut into 6 slices per pizza. This equates to four whole pizzas and one slice remaining from a pizza divided into six.
Mathematical Principles Involved
Several key mathematical principles are at play when working with 75/18:
- Fractions as Ratios: Fractions represent ratios, showing the relationship between two quantities.
- Greatest Common Divisor (GCD): Finding the GCD is crucial for simplifying fractions to their lowest terms. This ensures the most concise representation of the fraction's value.
- Improper Fractions and Mixed Numbers: Understanding the distinction and conversion between these forms is fundamental for solving various mathematical problems.
- Division: The process of converting an improper fraction to a mixed number involves division, a core arithmetic operation.
- Equivalence: The simplified fraction 25/6 and the original fraction 75/18 are equivalent; they represent the same value.
Decimal Representation of 75/18
To express 75/18 as a decimal, perform the division: 75 ÷ 18 ≈ 4.1667. This decimal representation provides another way to understand the value of the fraction. Note that this decimal is a repeating decimal, indicated by the overline (usually) above the repeating digits.
Applications of 75/18 and Similar Fractions
Understanding fractions is essential in numerous real-world applications:
- Baking: Recipes often use fractions to specify ingredient quantities.
- Construction: Measurements and material calculations frequently involve fractions.
- Finance: Working with percentages and proportions involves fractional concepts.
- Data Analysis: Fractions are used to represent proportions and ratios in datasets.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying fractions important?
A1: Simplifying fractions makes them easier to understand and work with. It presents the fraction in its most concise and efficient form.
Q2: Can I simplify a fraction by dividing the numerator and denominator by any number?
A2: No, you must divide both the numerator and the denominator by a common factor. Ideally, use the greatest common factor for the most simplified result.
Q3: What if the remainder is zero when converting an improper fraction to a mixed number?
A3: If the remainder is zero, it means the improper fraction is a whole number. There is no fractional part in the mixed number.
Q4: Are 75/18 and 25/6 the same fraction?
A4: Yes, they are equivalent fractions, representing the same value. 25/6 is simply the simplified form of 75/18.
Q5: How do I convert a mixed number back to an improper fraction?
A5: To convert a mixed number (e.g., 4 1/6) to an improper fraction, multiply the whole number (4) by the denominator (6), add the numerator (1), and place the result over the original denominator. This gives (4*6 + 1)/6 = 25/6.
Conclusion: Mastering Fractions
This detailed exploration of the fraction 75/18 illustrates the importance of understanding fundamental mathematical concepts. By mastering the skills of simplification, conversion between improper fractions and mixed numbers, and visual representation, you gain a solid foundation for tackling more complex mathematical challenges. Remember that practice is key to solidifying your understanding of fractions and their applications in various fields. The ability to work confidently with fractions like 75/18 will undoubtedly enhance your mathematical skills and problem-solving capabilities. Continue practicing, exploring different approaches, and don't hesitate to revisit these concepts as needed. With consistent effort, you'll become proficient in working with fractions and build a strong mathematical foundation.
Latest Posts
Latest Posts
-
210c In F
Sep 25, 2025
-
75 Of 10
Sep 25, 2025
-
5 Of 520
Sep 25, 2025
-
Dragon Vs Dinosaur
Sep 25, 2025
-
9 Power 3
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.