75 Of 160
interactiveleap
Sep 17, 2025 · 5 min read
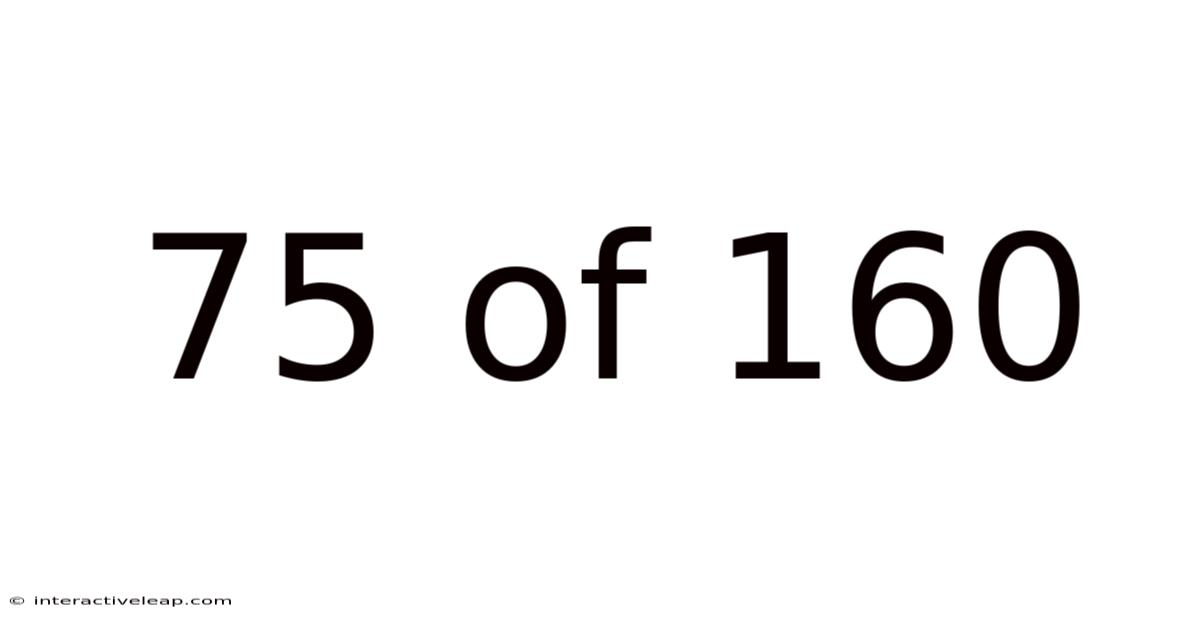
Table of Contents
Decoding the Fraction 75/160: A Comprehensive Guide to Understanding, Simplifying, and Applying Fractions
Understanding fractions is a fundamental skill in mathematics, crucial for everything from basic arithmetic to advanced calculus. This article delves deep into the fraction 75/160, exploring its simplification, decimal representation, percentage equivalent, and real-world applications. We'll go beyond simple calculation and explore the underlying principles, making this a valuable resource for students and anyone looking to strengthen their fractional understanding. Whether you're struggling with fractions or aiming to master them, this guide will provide a clear and comprehensive explanation.
Introduction: What is 75/160?
The fraction 75/160 represents a part of a whole. The number 75 is the numerator, indicating the number of parts we have, while 160 is the denominator, representing the total number of equal parts in the whole. At first glance, this fraction might seem complex, but through simplification and understanding its different representations, we can make it much easier to work with. This guide will equip you with the tools to confidently handle this and similar fractions.
1. Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before we delve into other representations, simplifying the fraction is crucial. Simplification involves reducing the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both 75 and 160 without leaving a remainder.
To find the GCD, we can use the Euclidean algorithm or prime factorization. Let's use prime factorization:
- Prime factorization of 75: 3 x 5 x 5 = 3 x 5²
- Prime factorization of 160: 2 x 2 x 2 x 2 x 2 x 5 = 2⁵ x 5
The common factor between 75 and 160 is 5. Therefore, the GCD is 5.
Now, we divide both the numerator and the denominator by 5:
75 ÷ 5 = 15 160 ÷ 5 = 32
Therefore, the simplified fraction is 15/32. This simplified form is much easier to work with in various calculations and comparisons.
2. Converting to Decimal: From Fraction to Decimal Representation
Converting a fraction to a decimal involves dividing the numerator by the denominator. Using a calculator or long division, we can find the decimal equivalent of 15/32:
15 ÷ 32 ≈ 0.46875
This decimal representation is useful for calculations involving decimals and for comparisons with other decimal numbers.
3. Expressing as a Percentage: Understanding Proportions
Percentages are a common way to represent fractions, particularly in contexts like discounts, grades, and statistics. To convert a fraction to a percentage, we first convert it to a decimal and then multiply by 100:
0.46875 x 100 = 46.875%
This means that 75/160 represents 46.875% of a whole.
4. Real-World Applications: Seeing Fractions in Action
Fractions are everywhere in our daily lives. Let's consider a few scenarios where understanding 75/160 (or its simplified form 15/32) would be useful:
-
Cooking: Imagine a recipe that calls for 160 grams of flour, and you only want to make a smaller portion using 75 grams. The fraction 75/160 represents the proportion of the original recipe you're making. Simplifying this to 15/32 makes it easier to adjust other ingredients proportionally.
-
Surveys and Statistics: Suppose a survey of 160 people showed that 75 preferred a particular product. The fraction 75/160 (or 15/32) would represent the proportion of people who preferred that product. This can be expressed as a percentage (46.875%) for easier interpretation.
-
Construction and Measurement: In construction or engineering, fractions are essential for precise measurements. Imagine a project where a total length of 160 centimeters needs to be divided, and a segment of 75 centimeters is required. The fraction 75/160 represents the proportion of the total length that segment occupies.
-
Financial Calculations: Fractions are frequently used in financial contexts. For instance, understanding fractional shares in the stock market or calculating proportions of investments requires a strong understanding of fractions and their manipulation.
5. Further Exploration: Advanced Concepts
Beyond basic simplification and conversion, let's explore some advanced concepts related to 75/160:
-
Equivalent Fractions: Many fractions are equivalent to 75/160. For example, 150/320, 225/480, and so on. These fractions all represent the same proportion, but 15/32 is the simplest form.
-
Improper Fractions and Mixed Numbers: While 75/160 is a proper fraction (numerator < denominator), if the numerator were larger than the denominator, it would be an improper fraction. Improper fractions can be converted into mixed numbers, which combine a whole number and a proper fraction.
-
Operations with Fractions: Understanding how to add, subtract, multiply, and divide fractions is crucial. These operations are essential for solving various mathematical problems involving fractions.
-
Fraction Comparisons: Being able to compare fractions is vital. For example, you might need to determine whether 75/160 is greater than, less than, or equal to another fraction.
6. Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 75/160?
A: The simplest form is 15/32.
-
Q: How do I convert 75/160 to a decimal?
A: Divide 75 by 160 using a calculator or long division (resulting in approximately 0.46875).
-
Q: How do I convert 75/160 to a percentage?
A: Convert it to a decimal (0.46875) and multiply by 100 (resulting in 46.875%).
-
Q: Are there any other fractions equivalent to 75/160?
A: Yes, infinitely many. Any fraction obtained by multiplying both the numerator and denominator by the same number will be equivalent.
-
Q: How do I add or subtract fractions like 75/160?
A: To add or subtract fractions, they must have a common denominator. If they don't, you need to find the least common multiple (LCM) of their denominators and convert the fractions accordingly.
7. Conclusion: Mastering Fractions for a Brighter Future
Understanding fractions is a fundamental building block for success in mathematics and various real-world applications. This detailed exploration of 75/160 has demonstrated how to simplify, convert, and apply this specific fraction, but the principles learned here are broadly applicable to all fractions. By mastering these concepts and practicing regularly, you'll build a strong foundation for future mathematical endeavors and confidently tackle any fractional challenges that come your way. Remember that consistent practice is key to mastering fractions – so grab a pencil, work through some examples, and watch your fractional fluency soar!
Latest Posts
Latest Posts
-
68inches In Cm
Sep 17, 2025
-
Slide Board Transfer
Sep 17, 2025
-
Demand Characteristics Psychology
Sep 17, 2025
-
10 Of 9000
Sep 17, 2025
-
16 Square Feet
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 160 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.