72 Of 25
interactiveleap
Sep 23, 2025 · 5 min read
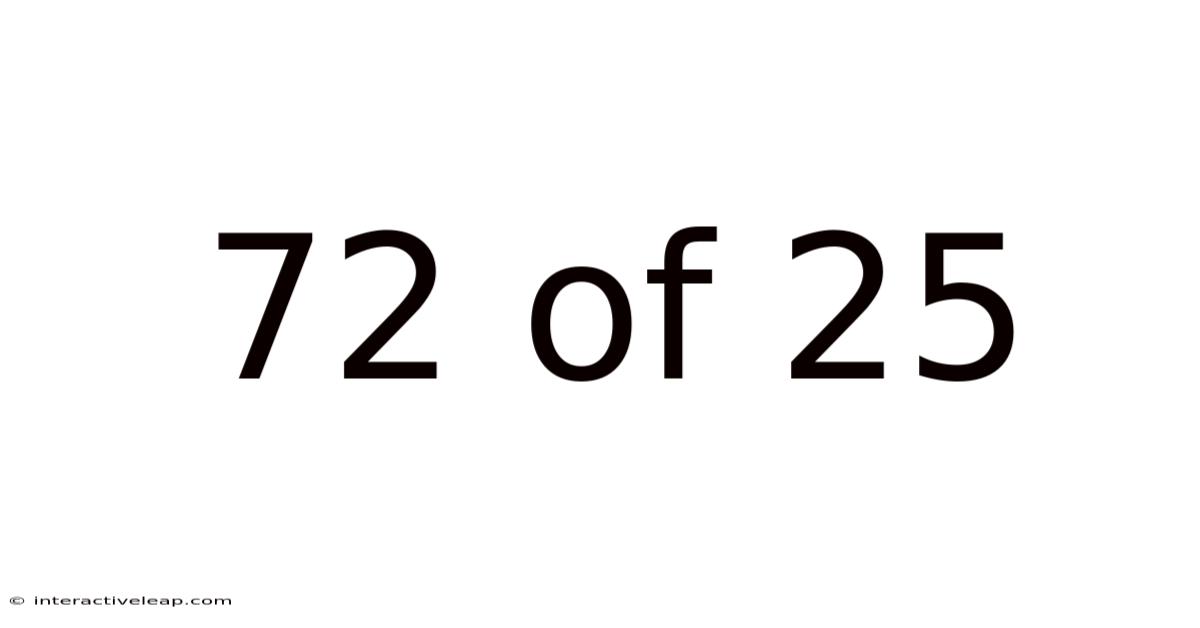
Table of Contents
Decoding the Enigma: Understanding 72/25 and its Applications
The fraction 72/25, seemingly simple at first glance, unveils a wealth of mathematical concepts and practical applications when explored in depth. This seemingly innocuous fraction is more than just a numerical expression; it's a gateway to understanding concepts like decimal conversion, percentage calculation, ratio analysis, and even its potential use in specific real-world scenarios. This article delves into the multifaceted nature of 72/25, providing a comprehensive understanding suitable for students, educators, and anyone curious about the power hidden within seemingly simple fractions.
Understanding the Basics: Fraction Decomposition
Before we embark on exploring the deeper implications of 72/25, let's revisit the fundamental concepts of fractions. A fraction represents a part of a whole. In 72/25, 72 is the numerator (the top number), representing the number of parts we have, and 25 is the denominator (the bottom number), representing the total number of equal parts the whole is divided into.
One crucial aspect of working with fractions is simplification. We can simplify a fraction by finding the greatest common divisor (GCD) of both the numerator and the denominator and dividing both by it. In this case, the GCD of 72 and 25 is 1 (they share no common factors other than 1). Therefore, 72/25 is already in its simplest form.
Converting to Decimal: Unveiling the Decimal Equivalent
Converting a fraction to a decimal is a straightforward process involving division. To find the decimal equivalent of 72/25, we simply divide 72 by 25:
72 ÷ 25 = 2.88
Therefore, 72/25 is equal to 2.88. This decimal representation is often more practical for certain calculations and comparisons.
Percentage Conversion: Expressing the Fraction as a Percentage
Percentages are a common way to express parts of a whole, particularly in contexts like statistics, finance, and everyday life. To convert 72/25 to a percentage, we first convert it to a decimal (as shown above: 2.88) and then multiply by 100:
2.88 × 100 = 288%
This means that 72/25 represents 288% of the whole. A percentage greater than 100% indicates that the numerator is larger than the denominator, signifying a value greater than the whole. This is perfectly valid mathematically and has practical implications in scenarios involving growth or increase.
Ratio Analysis: Exploring the Relationship between 72 and 25
The fraction 72/25 can also be interpreted as a ratio, expressing the relationship between two quantities. It indicates that for every 25 units of one quantity, there are 72 units of another. This concept is widely used in various fields:
- Business and Finance: Ratio analysis is crucial for evaluating financial health, profitability, and efficiency. For example, the ratio of revenue to expenses can be expressed as a fraction.
- Science and Engineering: Ratios are used to express proportions, concentrations, and scales in scientific experiments and engineering designs.
- Cooking and Baking: Recipes often utilize ratios to ensure consistent results. The ratio of ingredients is essential for achieving the desired outcome.
Real-World Applications: Exploring Practical Scenarios
The fraction 72/25, while seemingly abstract, finds applications in diverse real-world scenarios. Here are a few examples:
- Profit Calculation: Imagine a business with initial investment of 25 units and a profit of 72 units. The profit margin would be 72/25, indicating a significant return on investment (ROI).
- Growth Percentage: If a company's sales increased from 25 units to 72 units, the growth percentage would be 288%, demonstrating substantial expansion.
- Scaling and Proportions: In construction or design, the ratio 72/25 might represent the scaling factor for enlarging a blueprint.
Mathematical Explorations: Beyond the Basics
Let's delve deeper into the mathematical properties of 72/25:
- Continued Fractions: 72/25 can be expressed as a continued fraction, a unique representation of rational numbers. The process involves repeated division and obtaining integer quotients and remainders.
- Approximations: In situations where high precision isn't crucial, 72/25 can be approximated to simplify calculations. For instance, it can be rounded to 3 for quick estimations.
- Modular Arithmetic: This fraction can be used in modular arithmetic, a branch of mathematics dealing with remainders after division.
Frequently Asked Questions (FAQ)
Q: Can 72/25 be further simplified?
A: No. The greatest common divisor (GCD) of 72 and 25 is 1, meaning the fraction is already in its simplest form.
Q: What is the reciprocal of 72/25?
A: The reciprocal is obtained by swapping the numerator and the denominator: 25/72.
Q: How do I convert 72/25 to a mixed number?
A: To convert to a mixed number, divide the numerator (72) by the denominator (25). The quotient (2) becomes the whole number part, the remainder (22) becomes the new numerator, and the denominator (25) remains the same. Therefore, 72/25 = 2 22/25.
Conclusion: The Significance of a Simple Fraction
The seemingly simple fraction 72/25 reveals a depth of mathematical concepts and practical applications. From basic decimal and percentage conversions to more advanced ratio analysis and real-world problem-solving, understanding this fraction provides a strong foundation in numerical literacy. Its exploration highlights the interconnectedness of various mathematical ideas and demonstrates the importance of appreciating the potential within even the most straightforward numerical expressions. The versatility of 72/25 extends beyond simple arithmetic, illustrating its significance in diverse fields, making it a compelling example of how seemingly basic concepts can unlock a deeper understanding of the world around us. By mastering the principles demonstrated here, individuals can enhance their problem-solving abilities and confidently navigate various numerical challenges in their academic and professional pursuits.
Latest Posts
Latest Posts
-
Cotton In Spanish
Sep 23, 2025
-
Hair Extension Techniques
Sep 23, 2025
-
20 Of 575
Sep 23, 2025
-
32 3 4
Sep 23, 2025
-
48 3kg In Stone
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 72 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.