70 Of 10
interactiveleap
Sep 14, 2025 · 6 min read
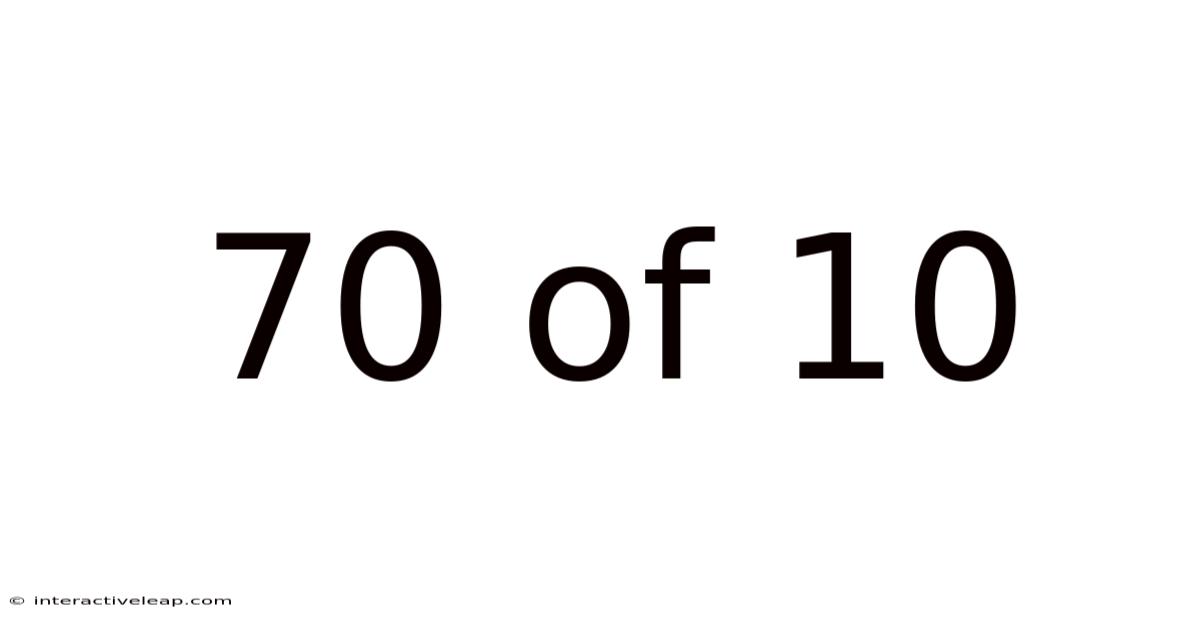
Table of Contents
Decoding the Fraction 70/10: A Comprehensive Guide
Understanding fractions is a fundamental skill in mathematics, crucial for various aspects of life, from baking a cake to calculating financial investments. This article delves into the seemingly simple fraction 70/10, exploring its various representations, applications, and the broader mathematical concepts it exemplifies. We'll move beyond a simple answer to provide a comprehensive understanding, making it suitable for students, educators, and anyone seeking a deeper grasp of fractions.
Introduction: What is 70/10?
The fraction 70/10 represents seventy parts out of a total of ten equal parts. At first glance, it might seem complex, but we'll soon see how straightforward it is to simplify and understand. This seemingly basic fraction provides an excellent opportunity to explore key concepts in arithmetic, including simplification, conversion to decimals and percentages, and real-world applications. We’ll cover these aspects in detail, ensuring a clear and complete understanding.
Simplifying the Fraction:
The most immediate step in working with 70/10 is simplification. Simplification means reducing the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator (70) and the denominator (10). The GCD is the largest number that divides both 70 and 10 without leaving a remainder. In this case, the GCD of 70 and 10 is 10.
To simplify:
- Divide both the numerator and the denominator by the GCD (10): 70 ÷ 10 = 7 and 10 ÷ 10 = 1.
- This simplifies the fraction 70/10 to 7/1.
This simplified fraction, 7/1, represents the same value as 70/10. Any fraction with a denominator of 1 is simply the whole number in the numerator. Therefore, 70/10 simplifies to 7.
Converting to a Decimal:
Fractions and decimals are closely related. To convert 70/10 to a decimal, simply perform the division: 70 ÷ 10 = 7.0. Therefore, 70/10 is equivalent to the decimal 7.0. This shows the direct relationship between fractions and decimals, emphasizing their interchangeability in representing quantities.
Converting to a Percentage:
Percentages are another way to express fractions and decimals, often used to represent proportions or rates. To convert 70/10 to a percentage, first convert it to a decimal (7.0), then multiply by 100 and add the percent symbol: 7.0 x 100% = 700%. However, this result of 700% may seem counterintuitive at first glance. Remember that a percentage represents a part of a whole (100%). Since 70/10 simplifies to 7, this indicates that 70/10 represents 700% of 10. To clarify, it's seven times the value of the whole. The significance here is understanding that percentages are always relative to a base, in this case, 10. This conversion highlights the need for careful consideration when dealing with percentages, particularly those exceeding 100%.
Real-World Applications:
The fraction 70/10, and its simplified form 7, has numerous practical applications:
- Dividing Objects: Imagine you have 70 candies to distribute equally among 10 children. Each child would receive 7 candies (70/10 = 7).
- Measuring Lengths: If you have a 70-meter long rope and you need to cut it into 10 equal pieces, each piece would be 7 meters long (70/10 = 7).
- Calculating Averages: If you scored 70 points out of a possible 10 points on a test (perhaps a weighted section), your score represents 7 times the maximum possible score. This unusual result would require reviewing the scoring system for this specific test.
- Financial Calculations: Imagine a scenario involving shares. If you own 70 shares out of a total of 10 shares (again, an unusual scenario suggesting an error in the data), the calculation would highlight the data discrepancy.
Mathematical Concepts Illustrated:
The fraction 70/10 provides a simple yet effective illustration of several important mathematical concepts:
- Equivalent Fractions: 70/10 and 7/1 are equivalent fractions; they represent the same value. This understanding is crucial for simplifying fractions and solving equations.
- Greatest Common Divisor (GCD): Finding the GCD is essential for simplifying fractions to their lowest terms, making calculations easier and results clearer.
- Improper Fractions: Although not strictly an improper fraction in the sense it doesn't have a numerator larger than the denominator after simplification, 70/10 highlights the concept of a fraction representing a value greater than one.
- Division: Converting fractions to decimals directly demonstrates the connection between division and fractions. A fraction essentially represents a division problem.
Further Exploration: Extending the Concept
Let's extend our understanding by considering similar fractions and exploring related concepts:
-
Fractions with larger numerators and denominators: Imagine fractions like 700/100 or 7000/1000. These fractions, although larger in value, simplify to the same whole number: 7. This reinforces the principle of equivalent fractions and the importance of simplification.
-
Fractions with different denominators: Comparing fractions such as 70/10 and 35/5 illustrates the concept of equivalent fractions with different representations. Both simplify to 7, demonstrating the flexibility in representing numerical values.
-
Mixed Numbers: Although 70/10 doesn't directly translate to a mixed number (a whole number and a fraction), it can be used to illustrate the concept. For example, 70/5 equals 14, which could be written as 14/1 or expressed as 14. This helps establish the relationship between fractions, decimals, and whole numbers.
Frequently Asked Questions (FAQ):
-
Q: Why is simplifying fractions important? A: Simplifying fractions makes them easier to understand and work with. It allows for easier comparison with other fractions and simplifies calculations.
-
Q: What if the GCD isn't easily identifiable? A: There are methods like prime factorization to find the GCD of larger numbers. Prime factorization helps break down a number into its prime factors, allowing you to identify the common factors and subsequently, the GCD.
-
Q: How can I convert any fraction to a decimal? A: Divide the numerator by the denominator. The result is the decimal equivalent of the fraction.
-
Q: What does it mean if a percentage is greater than 100%? A: A percentage greater than 100% indicates a value that exceeds the original base value. It represents more than the whole. In our example, 700% relative to 10 means seven times the value of 10.
-
Q: Are there any online tools to simplify fractions? A: Yes, numerous online calculators and websites are available for simplifying fractions, calculating GCDs, and converting between fractions, decimals, and percentages.
Conclusion: Mastering the Basics
The seemingly simple fraction 70/10 offers a valuable opportunity to reinforce foundational mathematical concepts. Through simplification, conversion to decimals and percentages, and practical applications, we've demonstrated the interconnectedness of different numerical representations. Understanding fractions is crucial for various fields, from everyday tasks to advanced mathematical studies. By mastering the basics, we build a solid foundation for tackling more complex mathematical challenges in the future. The exploration of 70/10, therefore, serves as more than just a simple calculation; it's a gateway to a deeper appreciation of the elegance and utility of mathematical principles. Remember to always simplify fractions whenever possible to ensure clarity and efficiency in your calculations. This understanding will empower you to confidently tackle future mathematical endeavors.
Latest Posts
Latest Posts
-
61 8kg In Stone
Sep 14, 2025
-
135 Pounds Kg
Sep 14, 2025
-
95 4kg In Stone
Sep 14, 2025
-
Opposite Of Diatribe
Sep 14, 2025
-
Cosmetic Travel Mirror
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 70 Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.