65 Of 140
interactiveleap
Sep 25, 2025 · 7 min read
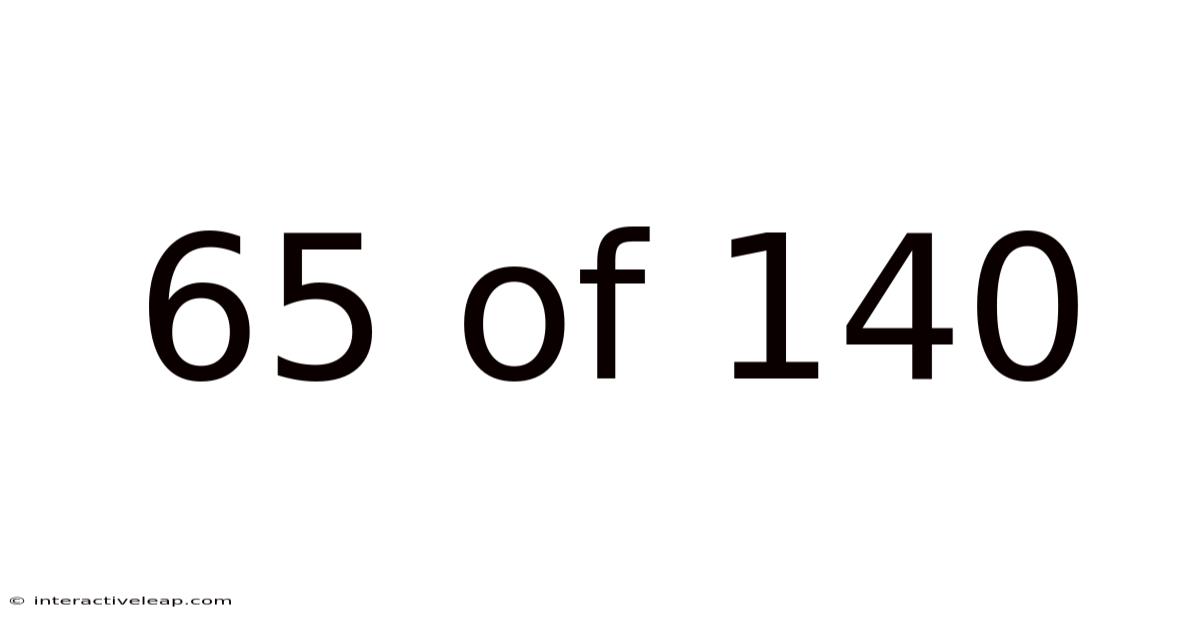
Table of Contents
Decoding the Fraction 65/140: A Comprehensive Guide to Simplification, Applications, and Understanding Fractions
Understanding fractions is a cornerstone of mathematical literacy. While seemingly simple at first glance, fractions hold a wealth of applications across various fields, from baking and construction to advanced calculus and scientific research. This article delves deep into the specific fraction 65/140, exploring its simplification, practical applications, and the broader concepts surrounding fractional arithmetic. We'll break down the process in a way that's accessible to everyone, regardless of their mathematical background. This comprehensive guide will equip you with the tools to not only understand 65/140 but also confidently approach other fractional calculations.
Introduction to Fractions: A Quick Refresher
Before we dive into the specifics of 65/140, let's briefly review the fundamental concepts of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole. For instance, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) represents two parts that make up a whole.
Fractions can be proper (numerator is less than the denominator, e.g., 1/2), improper (numerator is greater than or equal to the denominator, e.g., 3/2), or mixed numbers (a combination of a whole number and a proper fraction, e.g., 1 1/2). Understanding these distinctions is crucial for working with fractions effectively.
Simplifying 65/140: Finding the Greatest Common Divisor (GCD)
The fraction 65/140 isn't in its simplest form. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
To find the GCD of 65 and 140, we can use several methods:
-
Listing Factors: List all the factors of 65 (1, 5, 13, 65) and 140 (1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140). The greatest common factor is 5.
-
Prime Factorization: Break down both numbers into their prime factors.
- 65 = 5 x 13
- 140 = 2 x 2 x 5 x 7 = 2² x 5 x 7
The common prime factor is 5. Therefore, the GCD is 5.
Now, we divide both the numerator and the denominator of 65/140 by 5:
65 ÷ 5 = 13 140 ÷ 5 = 28
Therefore, the simplified form of 65/140 is 13/28. This is the simplest form because 13 and 28 share no common factors other than 1.
Converting Fractions to Decimals and Percentages
Fractions can be easily converted to decimals and percentages. To convert a fraction to a decimal, simply divide the numerator by the denominator.
13 ÷ 28 ≈ 0.464
To convert a decimal to a percentage, multiply by 100:
0.464 x 100 = 46.4%
Therefore, 65/140, or its simplified form 13/28, is approximately equal to 0.464 or 46.4%.
Practical Applications of 65/140 (and Fractions in General)
Fractions are pervasive in everyday life and across various disciplines. While 65/140 might not be a fraction you encounter daily in a specific context, understanding its simplification and conversion helps illustrate the broader application of fractional arithmetic.
Here are a few examples:
-
Baking: Recipes often use fractions to specify ingredient quantities (e.g., 1/2 cup of sugar, 2/3 cup of flour). Understanding fractions is essential for accurate baking.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Fractions are used in blueprints, calculations, and material estimations.
-
Finance: Interest rates, stock prices, and financial ratios are often expressed as fractions or decimals derived from fractions.
-
Data Analysis: Fractions and percentages (derived from fractions) are vital for presenting and interpreting data in various fields, including science, economics, and market research. For example, understanding that 65 out of 140 people prefer a certain product is expressed by the fraction 65/140 and simplifies the communication of that data.
-
Probability and Statistics: The foundation of probability and statistical analysis heavily relies on fractions and their representations. The likelihood of an event occurring is often represented as a fraction.
-
Scientific Measurements: In many scientific disciplines, measurements are frequently expressed in fractional form to denote precision and accuracy.
Adding, Subtracting, Multiplying, and Dividing Fractions
Working with fractions involves understanding the basic arithmetic operations. Here's a brief overview:
-
Addition and Subtraction: To add or subtract fractions, they must have a common denominator. If they don't, you need to find the least common multiple (LCM) of the denominators and convert the fractions accordingly.
-
Multiplication: Multiplying fractions is straightforward. Multiply the numerators together and the denominators together. Simplify the resulting fraction if necessary.
-
Division: To divide fractions, invert the second fraction (reciprocal) and multiply.
Let's illustrate with examples using 13/28 (the simplified form of 65/140) and another fraction, say 1/4:
-
Addition: To add 13/28 and 1/4, we need a common denominator (which is 28). 1/4 becomes 7/28. Therefore, 13/28 + 7/28 = 20/28. This simplifies to 5/7.
-
Subtraction: 13/28 - 7/28 = 6/28, which simplifies to 3/14.
-
Multiplication: 13/28 x 1/4 = 13/112
-
Division: 13/28 ÷ 1/4 = 13/28 x 4/1 = 13/7 (improper fraction, which can be expressed as 1 6/7 as a mixed number)
Frequently Asked Questions (FAQ)
Q1: What are some real-world scenarios where I might encounter a fraction like 65/140?
While 65/140 itself might not be frequently encountered in a specific, everyday context, it represents a broader class of fractions that appear regularly. Imagine a survey where 65 out of 140 respondents answered “yes” to a question. The fraction would represent the proportion of “yes” responses. The principles of simplifying and interpreting such fractions are crucial.
Q2: How can I improve my understanding and skills in working with fractions?
Practice is key. Start with simple fractions and gradually work towards more complex ones. Utilize online resources, educational videos, and worksheets to reinforce your understanding.
Q3: Are there any online tools or calculators that can help simplify fractions?
Yes, many online calculators and websites can simplify fractions. Simply enter the numerator and denominator, and the calculator will provide the simplified fraction. However, understanding the underlying process of finding the GCD is crucial for building a solid mathematical foundation.
Q4: What if the fraction has very large numbers? How do I find the GCD efficiently?
For very large numbers, the Euclidean algorithm is an efficient method to find the GCD. This algorithm involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
Q5: Is there a difference between simplifying a fraction and reducing a fraction?
No, simplifying and reducing a fraction are essentially the same process—reducing the fraction to its lowest terms by dividing the numerator and denominator by their greatest common divisor.
Conclusion: Mastering Fractions – A Lifelong Skill
Understanding fractions is a fundamental skill that extends far beyond the classroom. From everyday tasks to complex scientific calculations, the ability to work confidently with fractions is invaluable. This exploration of 65/140 has served as a springboard to understanding the broader concepts of simplification, conversion, and the practical applications of fractions. By mastering these principles, you equip yourself with a powerful tool for navigating the mathematical world and tackling numerous real-world challenges. Remember that consistent practice and a clear understanding of the underlying concepts are the keys to success in mastering fractions. Don’t be afraid to explore further, and always strive to build your mathematical understanding.
Latest Posts
Latest Posts
-
Weeds Are Flowers
Sep 25, 2025
-
20mph In Km
Sep 25, 2025
-
5x 12 0
Sep 25, 2025
-
210c In F
Sep 25, 2025
-
75 Of 10
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 65 Of 140 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.