60 X 0.3
interactiveleap
Sep 18, 2025 · 5 min read
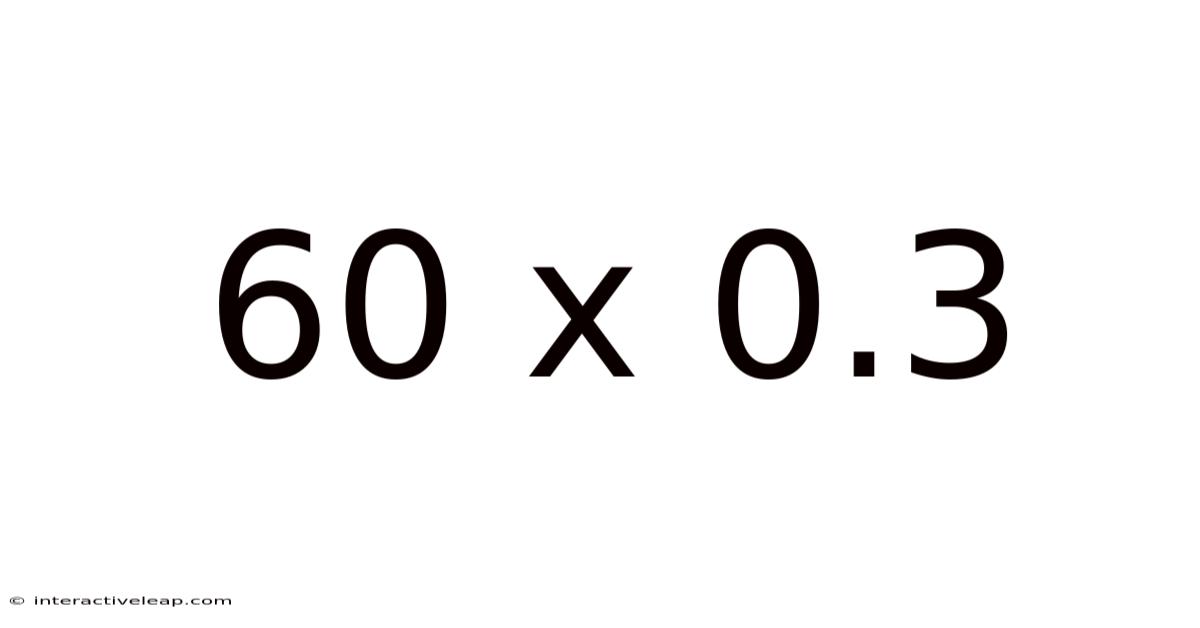
Table of Contents
Decoding 60 x 0.3: A Deep Dive into Multiplication and Decimal Understanding
This article explores the seemingly simple calculation of 60 x 0.3, delving far beyond the immediate answer to uncover the underlying mathematical principles and practical applications. We'll examine the different methods for solving this problem, discuss the significance of decimals and their role in everyday life, and address common misconceptions surrounding multiplication with decimals. Understanding this seemingly basic calculation lays a crucial foundation for more complex mathematical concepts.
Understanding the Problem: 60 x 0.3
At its core, 60 x 0.3 represents a multiplication problem. We are tasked with finding the product of 60 and 0.3. While seemingly straightforward, this problem provides an excellent opportunity to explore different approaches to multiplication and solidify our understanding of decimals. The ability to confidently solve problems like this is essential for various applications, from calculating discounts and percentages to understanding financial statements and scientific measurements.
Method 1: Converting the Decimal to a Fraction
One effective method for solving 60 x 0.3 involves converting the decimal 0.3 into a fraction. Remember that 0.3 is equivalent to 3/10. Therefore, our problem transforms into:
60 x (3/10)
Multiplication of fractions involves multiplying the numerators (top numbers) and denominators (bottom numbers) separately. This gives us:
(60 x 3) / 10 = 180 / 10
Finally, simplifying the fraction, we get:
180 / 10 = 18
Therefore, 60 x 0.3 = 18.
Method 2: Using the Distributive Property
The distributive property of multiplication states that a(b + c) = ab + ac. We can use this property to break down the problem into smaller, more manageable parts. Since 0.3 can be expressed as 0.1 + 0.2 (or 0.1 x 3), we can apply the distributive property as follows:
60 x 0.3 = 60 x (0.1 x 3) = (60 x 0.1) x 3
We know that 60 x 0.1 is simply moving the decimal point one place to the left in 60, resulting in 6. Therefore:
6 x 3 = 18
Thus, 60 x 0.3 = 18. This method highlights the flexibility of mathematical operations and shows how breaking down a problem can simplify the calculation.
Method 3: Direct Decimal Multiplication
This method involves directly multiplying 60 by 0.3, aligning the numbers vertically. Remember to account for the decimal place in the final answer.
60
x 0.3
-----
180
-----
18.0
Notice that we initially multiply 60 by 3, ignoring the decimal point, which yields 180. Then, we count the total number of decimal places in the original numbers (one decimal place in 0.3). We place the decimal point in our answer (180) so that there's one decimal place, resulting in 18.0, or simply 18.
The Significance of Decimals in Everyday Life
Decimals are far from abstract mathematical concepts; they're integral to our daily lives. We encounter decimals in numerous contexts:
-
Finance: Calculating prices, discounts (like a 30% off sale), taxes, interest rates, and currency conversions all involve decimal numbers. Understanding decimals is crucial for managing personal finances effectively.
-
Measurement: Many measurements, whether it's length (centimeters, meters), weight (grams, kilograms), or volume (liters, milliliters), utilize decimal systems. Accurate measurements often require decimal precision.
-
Science: Scientific calculations, data analysis, and research rely heavily on decimals to represent precise measurements and values.
-
Technology: Computer programming, digital imaging, and various other technologies utilize decimal representation for data storage and manipulation.
Common Misconceptions about Decimal Multiplication
Several common misconceptions can hinder a thorough understanding of decimal multiplication. Addressing these misconceptions is crucial for mastering the concept:
-
Misplacement of the decimal point: A common mistake is misplacing the decimal point in the final answer. Students might forget to account for the total number of decimal places in the original numbers.
-
Ignoring the decimal altogether: Some students might treat the decimal as insignificant and perform the multiplication as if they were dealing with whole numbers. This leads to incorrect answers.
-
Difficulty visualizing decimals: Decimals, unlike whole numbers, are not always readily grasped visually. Understanding their fractional representation (0.3 = 3/10) can aid in better comprehension.
Frequently Asked Questions (FAQ)
Q: What if one of the numbers was a decimal with more than one decimal place?
A: The principle remains the same. Multiply the numbers as whole numbers, and then place the decimal point in the answer based on the total number of decimal places in the original numbers. For example, 60 x 0.35 would involve multiplying 60 by 35 and then placing the decimal point two places from the right (because 0.35 has two decimal places). This would yield 21.00 or 21.
Q: Can I use a calculator to solve this problem?
A: Yes, calculators can easily handle decimal multiplication. However, understanding the underlying mathematical principles is equally important, even when using a calculator. The calculator provides a quick solution, but the manual methods enhance your comprehension of the concepts.
Q: Are there other ways to represent 0.3?
A: Yes, 0.3 can be represented as a fraction (3/10), a percentage (30%), or even as a ratio (3:10). Understanding these different representations is vital for solving problems in various contexts.
Conclusion: Beyond the Calculation
The seemingly simple calculation of 60 x 0.3 provides a valuable opportunity to explore the fundamental concepts of multiplication, decimals, and their practical applications. Mastering this calculation strengthens your mathematical foundation and prepares you for more complex mathematical challenges in various fields. By understanding the different methods for solving this problem and addressing common misconceptions, you'll develop a stronger grasp of decimal arithmetic and improve your problem-solving skills. Remember that the key lies not just in obtaining the correct answer (18) but in comprehending the underlying mathematical principles that govern the calculation. This understanding will serve as a strong base for tackling more advanced mathematical problems in the future.
Latest Posts
Latest Posts
-
60 Divided 7
Sep 18, 2025
-
40 Of 135
Sep 18, 2025
-
93 Miles Km
Sep 18, 2025
-
6 Times 3
Sep 18, 2025
-
56kh In Stone
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 60 X 0.3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.